Why the rank-2 stress-energy tensor of general relativity does not imply a spin-2 graviton
“If it exists, the graviton must be massless (because the gravitational force has unlimited range) and must have a spin of 2 (because the source of gravity is the stress-energy tensor, which is a second-rank tensor, compared to electromagnetism, the source of which is the four-current, which is a first-rank tensor). To prove the existence of the graviton, physicists must be able to link the particle to the curvature of the space-time continuum and calculate the gravitational force exerted.” – False claim, Wikipedia.
Previous posts explaining why general relativity requires spin-1 gravitons, and rejects spin-2 gravitons, are linked here, here, here, here, and here. But let’s take the false claim that gravitons must be spin-2 because the stress-energy tensor is rank-2. A rank 1 tensor is a first-order (once differentiated, e.g. da/db) differential summation, such as the divergence operator (sum of field gradients) or curl operator (the sum of all of the differences in gradients between field gradients for each pair of mutually orthagonal directions in space). A rank 2 tensor is some defined summation over second-order (twice differentiated, e.g. d2a/db2) differential equations. The field equation of general relativity has a different structure from Maxwell’s field equations for electromagnetism: as the Wikipedia quotation above states, Maxwell’s equations of classical electromagnetism are vector calculus (rank-1 tensors or first-order differential equations), while the tensors of general relativity are second order differential equations, rank-2 tensors.
The lie, however, is that this is physically deep. It’s not. It’s purely a choice of how to express the fields conveniently. For simple electromagnetic fields, where there is no contraction of mass-energy by the field itself, you can do it easily with first-order equations, gradients. These equations calculate fields with a first-order (rank-1) gradient, e.g. electric field strength, which is the gradient of potential/distance, measured in volts/metre. Maxwell’s equations don’t directly represent accelerations (second-order, rank-2 equations would be needed for that). For gravitational fields, you have to work with accelerations because the gravitational field contracts the source of the gravitational field itself, so gravitation is more complicated than electromagnetism.
The people who promote the lie that because rank-1 tensors apply to spin-1 field quanta in electromagnetism, rank-2 tensors must imply spin-2 gravitons, offer no evidence of this assertion. It’s arm-waving lying. It’s true that you need rank-2 tensors in general relativity, but it is not necessary in principle to use rank-1 tensors in electromagnetism: it’s merely easiest to use the simplest mathematical method available. You could in principle use rank-2 tensors to rebuild electromagnetism, by modelling the equations to observable accelerations instead of unobservable rank-1 electric fields and magnetic fields. Nobody has ever seen an electric field: only accelerations and forces caused by charges. (Likewise for magnetic fields.)
There is no physical correlation between the rank of the tensor and the spin of the gauge boson. It’s a purely historical accident that rank-1 tensors (vector calculus, first-order differential equations) are used to model fictitious electric and magnetic “fields”. We don’t directly observe electric field lines or electric charges (nobody has seen the charged core of an electron, what we see are effects of forces and accelerations which can merely be described in terms of field lines and charges). We observe accelerations and forces. The field lines and charges are not directly observed. The mathematical framework for a description of the relationship between the source of a field and the end result depends on the definition of the end result. In Maxwell’s equations, the end result of a electric charge which is not moving relative to the observer is a first-order field, defined in volts/metre. If you convert this first-order differential field into an observable effect, like force or acceleration, you get a second-order differential equation, acceleration a = d2x/dt2. General relativity doesn’t describe gravity in terms of a first-order field like Maxwell’s equations do, but instead describes gravitation in terms of a second-order observable, i.e. space curvature produced acceleration, a = d2x/dt2.
So the distinction between rank-1 and rank-2 tensors in electromagnetism and general relativity is not physically deep: it’s a matter of human decisions on how to represent electromagnetism and gravitation.
We choose in Maxwell’s equations to represent not second-order accelerations but using Michael Faraday’s imaginary concept of a pictorial field, radiating and curving “field lines” which are represented by first-order field gradients and curls. In Einstein’s general relativity, by contrast, we don’t represent gravity by such half-baked unobservable field concept, but in terms of directly-observable accelerations.
Like first-quantization (undergraduate quantum mechanics) lies, the “spin-2” graviton deception is a brilliant example of historical physically-ignorant mathematical obfuscation in action, leading to groupthink delusions in theoretical physics. (Anyone who criticises the lie is treated with a similar degree of delusional, paranoid hostility directed to dissenters of evil dictatorships. Instead of examining the evidence and seeking to correct the problem – which in the case of an evil dictatorship is obviously a big challenge – the messenger is inevitably shot or the “message” is “peacefully” deleted from the arXiv, reminiscent of the scene from Planet of the Apes where Dr Zaius – serving a dual role as Minister of Science and Chief Defender of the Faith, has to erase the words written in the sand which would undermine his religion and social tea-party of lying beliefs. In this analogy, the censors of the arXiv or journals like Classical and Quantum Gravity are not defending objsctive science, but are instead defending subjective pseudo-science – the groupthink orthodoxy which masquerades as science – from being exposed as a fraud.)
Dissimilarities in tensor ranks used to describe two different fields originate from dissimilarities in the field definitions for those two different fields, not to the spin of the field quanta. Any gauge field whose field is written in a second order differential equation, e.g., acceleration, can be classically approximated by rank-2 tensor equation. Comparing Maxwell’s equations in which fields are expressed in terms of first-order gradients like electric fields (volts/metre) with general relativity in which fields are accelerations or curvatures, is comparing chalk and cheese. They are not just different units, but have different purposes. For a summary of textbook treatments of curvature tensors, see Dr Kevin Aylward’s General Relativity for Teletubbys: “the fundamental point of the Riemann tensor [the Ricci curvature tensor in the field equation general relativity is simply a cut-down, rank-2 version Riemann tensor: the Ricci curvature tensor, Rab = Rxaxb, where Rxaxb is the Riemann tensor], as far as general relativity is concerned, is that it describes the acceleration of geodesics with respect to one another. … I am led to believe that many people don’t have a … clue what’s going on, although they can apply the formulas in a sleepwalking sense. … The Riemann curvature tensor is what tells one what that acceleration between the [particles] will be. This is expressed by
[Beware of some errors in the physical understanding of some of these general relativity internet sites, however. E.g., some suggest – following a popular 1950s book on relativity – that the inverse-square law is discredited by general relativity, because the relativistic motion of Mercury around the sun can be approximated within Newton’s framework by increasing the inverse-square law power slightly from its value of 1/R2 to 1/R2 + X where X is a small fraction, so that the force appears to get stronger nearer the sun. This is fictitious and is just an approximation to roughly accommodate relativistic effects that Newton ignored, e.g. the small increase in planetary mass due to its higher velocity when the planet is nearer the sun on part of its elliptical orbit, than it has when it is moving slower far from sun. This isn’t a physically correct model; it’s just a back-of-the-envelope fudge. A physically correct version of planetary motion in the Newtonian framework would keep the geometric inverse square law and would then correctly modify the force by making the right changes for the relativistic mass variation with velocity. Ptolemy’s epicycles demonstrated the danger of constructing approximate mathematical model which have no physical validity, which then become fashion.]”
Maxwell’s theory based on Faraday’s field lines concept employs only rank-1 equations, for example the divergence of the electric field strength, E, is directly proportional to the charge density, q (charge density is here defined as the charge per unit surface area, not the charge per unit volume): div.E ~ q. The reason this is a rank-1 equation is simply because the divergence operator is the sum of gradients in all three perpendicular directions of space for the operand. All it says is that a unit charge contributes a fixed number of diverging radial lines of electric field, so the total field is directly proportional to the total charge.
But this is just Faraday’s way of visualizing the way the electric force operates! Remember that nobody has yet seen or reported detecting an “electric field line” of force! With our electric meters, iron filings, and compasses we only see the results of forces and accelerations, so the number and locations of electric or magnetic field lines depicted in textbook diagrams is due to purely arbitrary conventions. It’s merely an abstract aetherial legacy from the Faraday-Maxwell era, not a physical reality that has any experimental evidence behind it. If you are going to confuse Faraday’s and Maxwell’s imaginary concept of field “lines” with experimentally defensible reality, you might as well write down an equation in which the invisible intermediary between charge and force is an angel, a UFO, a fairy or an elephant in an imaginary extra dimension. Quantum field theory tells us that there are no physical lines. Instead of Maxwell’s “physical lines of force”, we have known since QED was verified that there are field quanta being exchanged between charges.
So if we get rid of our ad hoc prejudices, getting rid of “electric field strength, E” in volts/metre and just expressing the result of the electric force in terms of what we can actually measure, namely accelerations and forces, we’d have a rank-2 tensor, basically the same field equation as is used in general relativity for gravity. The only differences will be the factor of ~1040 difference between field strengths of electromagnetism and gravity, the differences in the signs for the curvatures (like charges repel in electromagnetism, but attract in gravity) and the absence of the contraction term that makes the gravitational field contract the source of the field, but supposedly does not exist in electromagnetism. The tensor rank will be 2 for both cases, thus disproving the arm-waving yet popular idea that the rank number may be correlated to the field quanta spin. In other words, the electric field could be modelled by a rank-2 equation if we simply make the electric field consistent with the gravitational field by expressing both field in terms of accelerations, instead of using the gradient of the Faraday-legacy volts/metre “field strength” for the electric field. This is however beyond the understanding of the mainstream, who are deluded by fashion and historical ad hoc conventions. Most of the problems in understanding quantum field theory and unifying Standard Model fields with gravitational fields result from the legacy of field definitions used in Maxwellian and Yang-Mills fields, which for purely ad hoc historical reasons are different from the field definition in general relativity. If all fields are expressed in the same way as accelerative curvatures, all field equations become rank-2 and all rank-1 divergencies automatically disappear, since are merely an historical legacy of the Faraday-Maxwell volts/metre field “line” concept, which isn’t consistent with the concept of acceleration due to curvature in general relativity!
However, we’re not advocating the use of any particular differential equations for any quantum fields, because discontinuous quantized fields can’t in principle be correctly modelled by differential equations, which is why you can’t properly represent the source of gravity in general relativity as being a set of discontinuities (particles) in space to predict curvature, but must instead use a physically false averaged distribution such as a “perfect fluid” to represent the source of the field. The rank-2 framework of general relativity has relatively few easily obtainable solutions compared to the simpler rank-1 (vector calculus) framework of electrodynamics. But both classical fields are false in ignoring the random field quanta responsible for quantum chaos (see, for instance, the discussion of first-quantization versus second-quantization in the previous post here, here and here).
Summary:
1. The electric field is defined by Michael Faraday as simply the gradient of volts/metre, which Maxwell correctly models with a first-order differential equation, which leads to a rank-1 tensor equation (vector calculus). Hence, electromagnetism with spin-1 field quanta has a rank-1 tensor purely because of the way it is formulated. Nobody has ever seen Faraday’s electric field, only accelerations/forces. There is no physical basis for electromagnetism being intrinsically rank-1; it’s just one way to mathematically model it, by describing it in terms of Faraday rank-1 fields rather than the directly observable rank-2 accelerations and forces which we see/feel.
2. The gravitational field has historically never been expressed in terms of a Faraday-type rank-1 field gradient. Due to Newton, who was less pictorial than Faraday, gravity has always been described and modelled directly in terms of the end result, i.e. accelerations/forces we see/feel.
This difference between the human formulations of the electromagnetic and gravitational “fields” is the sole reason for the fact that the former is currently expressed with a rank-1 tensor and the latter is expressed with a rank-2 tensor. If Newton had worked on electromagnetism instead of aether crackpots like Maxwell, we would undoubtedly have a rank-2 mathematical model of electromagnetism, in which electric fields are expressed not in volts/metre, but directly in terms of rank-2 acceleration (curvatures), just like general relativity.
Both electromagnetism and gravitation should define fields the same way, with rank-2 curvatures. The discrepancy that electromagnetism uses instead rank-1 tensors is due to the inconsistency that in electromagnetism fields are not defined in terms of curvatures (accelerations) but in terms of a Faraday’s imaginary abstraction of field lines. This has nothing whatsoever to do with particle spin. Rank-1 tensors are used in Maxwell’s equations because the electromagnetic fields are defined (inconsistently with gravity) in terms of rank-1 unobservable field gradients, whereas rank-2 tensors are used in general relativity purely because the definition of a field in general relativity is acceleration, which requires a rank-2 tensor to describe it. The difference is purely down to the way the field is described, not the spin of the field.
The physical basis for rank-2 tensors in general relativity
I’m going to rewrite the paper linked here when time permits.
Groupthink delusions
The real reason why gravitons supposedly “must” be spin-2 is due to the mainstream investment of energy and time in worthless string theory, which is designed to permit the existence of spin-2 gravitons. We know this because whenever the errors in spin-2 gravitons are pointed out, they are ignored. These stringy people aren’t interested in physics, just grandiose fashionable speculations, which is the story of Ptolemy’s epicycles, Maxwell’s aether, Kelvin’s vortex atom, Piltdown Man, S-matrices, UFOs, Marxism, fascism, etc. All were very fashionable with bigots in their day, but:
“… reality must take precedence over public relations, for nature cannot be fooled.” – Feynman’s Appendix F to Rogers’ Commission Report into the Challenger space shuttle explosion of 1986.

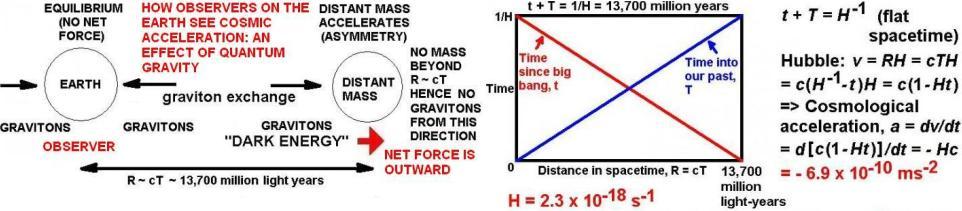
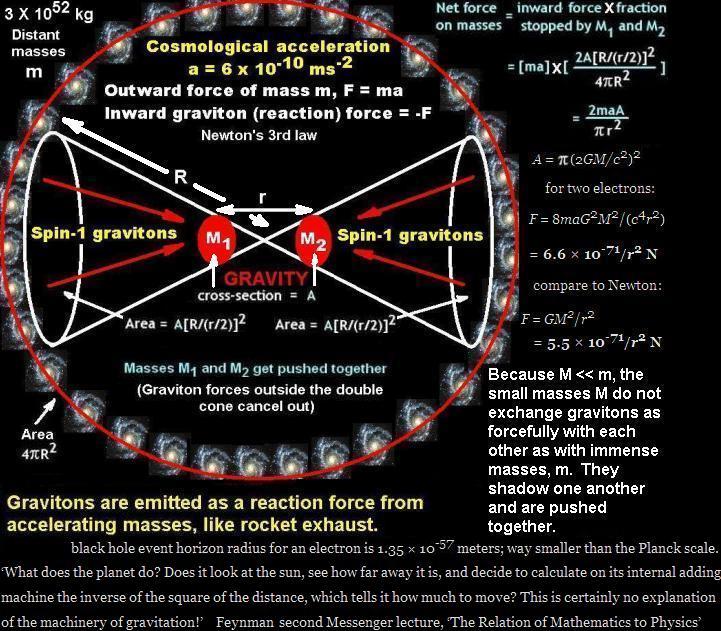
 Update (12 January 2010): around us, the accelerating mass of the universe causes an outward force that can be calculated by Newton’s 2nd law, which in turn gives an equal inward reaction force by Newton’s 3rd law. The fraction of that inward force which causes gravity is simply equal to the fraction of the effective surface area of the particle which is shadowed by relatively nearby, non-accelerating masses. If the distance R between the two particles is much larger than their effective radii r for graviton scatter (exchange), then by geometry the area of the shadow cast on surface area 4*Pi*r2 by the other fundamental particle is Pi*r4/R2, so the fraction of the total surface area of the particle which is shadowed is (Pi*r4/R2)/(4*Pi*r2) = (1/4)(r/R)2. This fraction merely has to be multiplied by the inward force generated by distant mass m undergoing radial outward observed cosmological acceleration a, i.e. force F = ma, in order to predict the gravitational force, which is not the same thing as LeSage’s non-factual, non-predictive gas shadowing (which is to quantum gravity what Lemarke’s theory was to Darwin’s evolution, or what Aristotle’s laws of motion were to Newton’s, i.e. mainly wrong). In other words, the source of gravity and dark energy is the same thing: spin-1 vacuum radiation. Spin-2 gravitons are a red-herring, originating from a calculation which assumed falsely that gravitons either would not be exchanged with distant masses, or that any effect would somehow cancel out or be negligible. Woit states:
Update (12 January 2010): around us, the accelerating mass of the universe causes an outward force that can be calculated by Newton’s 2nd law, which in turn gives an equal inward reaction force by Newton’s 3rd law. The fraction of that inward force which causes gravity is simply equal to the fraction of the effective surface area of the particle which is shadowed by relatively nearby, non-accelerating masses. If the distance R between the two particles is much larger than their effective radii r for graviton scatter (exchange), then by geometry the area of the shadow cast on surface area 4*Pi*r2 by the other fundamental particle is Pi*r4/R2, so the fraction of the total surface area of the particle which is shadowed is (Pi*r4/R2)/(4*Pi*r2) = (1/4)(r/R)2. This fraction merely has to be multiplied by the inward force generated by distant mass m undergoing radial outward observed cosmological acceleration a, i.e. force F = ma, in order to predict the gravitational force, which is not the same thing as LeSage’s non-factual, non-predictive gas shadowing (which is to quantum gravity what Lemarke’s theory was to Darwin’s evolution, or what Aristotle’s laws of motion were to Newton’s, i.e. mainly wrong). In other words, the source of gravity and dark energy is the same thing: spin-1 vacuum radiation. Spin-2 gravitons are a red-herring, originating from a calculation which assumed falsely that gravitons either would not be exchanged with distant masses, or that any effect would somehow cancel out or be negligible. Woit states:
“Many of the most well-known theorists are pursuing research programs with the remarkable features that:
“•You don’t need to have any idea what the fundamental degrees of freedom are.
“•You don’t need any fundamental dynamical laws either.
“•You can do everything with high school mathematics.”
Although making the most basic quantum gravity predictions can be done with “high school mathematics”, the deeper gauge symmetry connection of quantum gravity to the Standard Model of particle physics does require more advanced mathematics, as does the job of deriving a classical approximation (i.e. a corrected general relativity for cosmology) to this quantum gravity theory, for more detailed checks and predictions. When Herman Kahn was asked, at the 1959 congressional hearings on nuclear war, whether he agreed with the Atomic Energy Commission name of “Sunshine Unit” for strontium-90 levels in human bones, he replied that although he engaged in a number of controversies, he tried to keep the number down. He wouldn’t get involved. Doubtless, Woit has the same policy towards graviton spin. What I’m basically saying is that the fundamental particle is that causing cosmological repulsion, which has spin-1. This causes gravity as a “spin-off” (no pun intended). So if spin-1 gravitons are hard to swallow, simply name them instead spin-1 dark energy particles! Whatever makes the facts easier to digest…
Above: the latest illustration (updated 27 September 2009) which has replaced the older illustration included in the post below. Improvements have been made.
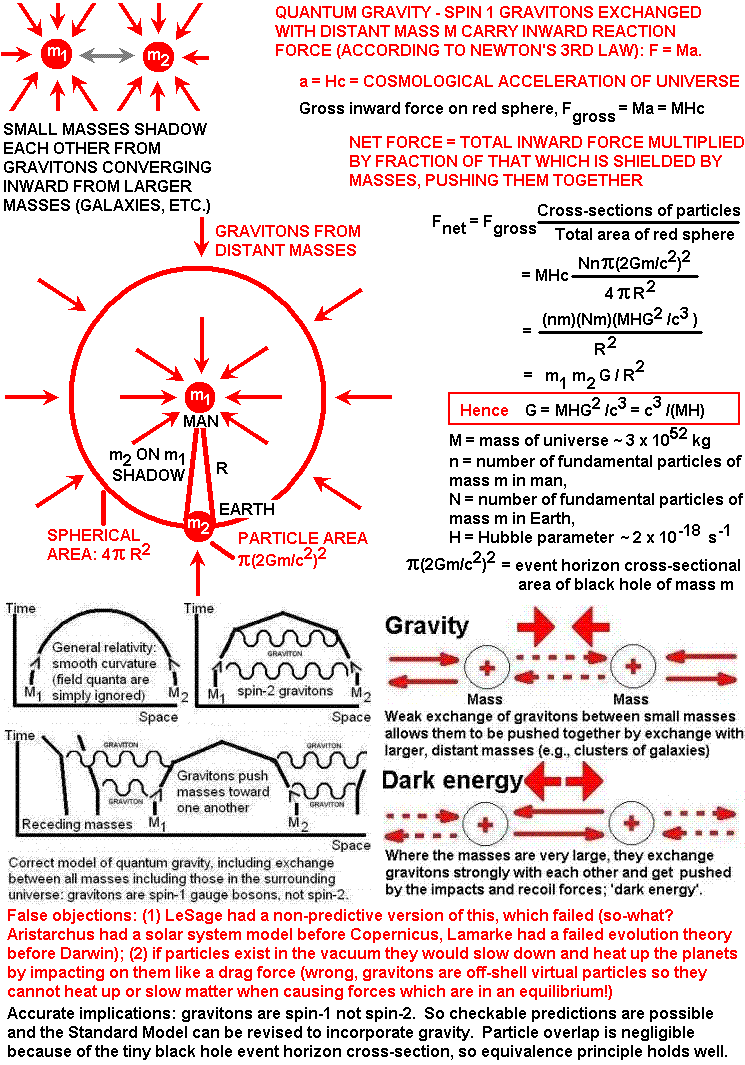
String ‘theory’ (abject uncheckable speculation) combines a non-experimentally justifiable speculation about forces unifying at the Planck scale, with another non-experimentally justifiable speculation that gravity is mediated by spin-2 particles which are only exchanged between the two masses in your calculation, and somehow avoid exchanging with the way bigger masses in the surrounding universe.
When you include in your path integral the fact that exchange gravitons coming from distant masses will be converging inwards towards an apple and the earth, it turns out that this exchange radiation with distant masses actually predominates over the local exchange and pushes the apple down to the earth, so it is easily proved that gravitons are spin-1 not spin-2.
The proof below also makes checkable predictions and tells us exactly how quantum gravity fits into the electroweak symmetry of the Standard Model alongside the other long range force at low energy, electromagnetism, thus altering the usual interpretation of the Standard Model symmetry groups and radically changing the nature of electroweak symmetry breaking from the usual poorly predictive mainstream Higgs field.
Professor Richard P. Feynman’s paper ‘Space-Time Approach to Non-Relativistic Quantum Mechanics’, Reviews of Modern Physics, volume 20, page 367 (1948), makes it clear that his path integrals are a censored explicit reformulation of quantum mechanics, not merely an extension to sweep away infinities in quantum field theory!
Richard P. Feynman explains in his book, QED, Penguin, 1990, pp. 55-6, and 84:
‘I would like to put the uncertainty principle in its historical place: when the revolutionary ideas of quantum physics were first coming out, people still tried to understand them in terms of old-fashioned ideas … But at a certain point the old fashioned ideas would begin to fail, so a warning was developed that said, in effect, “Your old-fashioned ideas are no damn good when …”. If you get rid of all the old-fashioned ideas and instead use the ideas that I’m explaining in these lectures – adding arrows [arrows = phase amplitudes in the path integral] for all the ways an event can happen – there is no need for an uncertainty principle! … on a small scale, such as inside an atom, the space is so small that there is no main path, no “orbit”; there are all sorts of ways the electron could go, each with an amplitude. The phenomenon of interference [by field quanta] becomes very important …’
Take the case of simple exponential decay: the mathematical exponential decay law predicts that the dose rate never reaches zero, so effective dose rate for exposure to an exponentially decaying source needs clarification: taking an infinite exposure time will obviously underestimate the dose rate regardless of the total dose, because any dose divided into an infinite exposure time will give a false dose rate of zero. Part of the problem here is that the exponential decay curve is false: it is based on calculus for continuous variations, and doesn’t apply to radioactive decay which isn’t continuous but is a discrete phenomenon. This mathematical failure undermines the interpretation of real events in quantum mechanics and quantum field theory, because discrete quantized fields are being falsely approximated by the use of the calculus, which ignores the discontinuous (lumpy) changes which actually occur in quantum field phenomena, e.g., as Dr Thomas Love of California State University points out, the ‘wavefunction collapse’ in quantum mechanics when a radioactive decay occurs is a mathematical discontinuity due to the use of continuously varying differential field equations to represent a discrete (discontinuous) transition!
[‘The quantum collapse [in the mainstream interpretation of quantum mechanics, where a wavefunction collapse occurs whenever a measurement of a particle is made] occurs when we model the wave moving according to Schroedinger (time-dependent) and then, suddenly at the time of interaction we require it to be in an eigenstate and hence to also be a solution of Schroedinger (time-independent). The collapse of the wave function is due to a discontinuity in the equations used to model the physics, it is not inherent in the physics.’ – Dr Thomas Love, Departments of Physics and Mathematics, California State University, ‘Towards an Einsteinian Quantum Theory’, preprint emailed to me.]
Alpha radioactive decay occurs when an alpha particle undergoes quantum tunnelling to escape from the nucleus through a ‘field barrier’ which should confine it perfectly, according to classical physics. But as Professor Bridgman explains, the classical field law falsely predicts a definite sharp limit on the distance of approach of charged particles, which is not observed in reality (in the real world, there is a more gradual decrease). The explanation for alpha decay and ‘quantum tunnelling’ is not that the mathematical laws are perfect and nature is ‘magical and beyond understanding’, but simply that the differential field law is just a statistical approximation and wrong at the fundamental level: electromagnetic forces are not continuous and steady on small scales, but are due to chaotic, random exchange radiation, which only averages out and approaches the mathematical ‘law’ over long distances or long times. Forces are actually produced by lots of little particles, quanta, being exchanged between charges.
On large scales, the effect of all these little particles averages out to appear like Coulomb’s simple law, just as on large scales, air pressure can appear steady, when in fact on small scales it is a random bombardment of air molecules which cause Brownian motion. On small scales, such as the distance between an alpha particle and other particles in the nucleus, the forces are not steady but fluctuate as the field quanta are randomly and chaotically exchanged between the nucleons. Sometimes it is stronger and sometimes weaker than the potential predicted by the mathematical law. When the field confining the alpha particle is weaker, the alpha particle may be able to escape, so there is no magic to ‘quantum tunnelling’. Therefore, radioactive decay only behaves the smooth exponential decay law as a statistical approximation for large decay rates. In general the exponential decay rate is false and for a nuclide of short half-life, all the radioactive atoms decay after a non-infinite time; the prediction of that ‘law’ that radioactivity continues forever is false.
There is a stunning lesson from human ‘groupthink’ arrogance today that Feynman’s fact-based physics is still censored out by mainstream string theory, despite the success of path integrals based on this field quanta interference mechanism!
Regarding string theory, Feynman said in 1988:
‘… I do feel strongly that this is nonsense! … I think all this superstring stuff is crazy and is in the wrong direction. … I don’t like it that they’re not calculating anything. I don’t like that they don’t check their ideas. I don’t like that for anything that disagrees with an experiment, they cook up an explanation … All these numbers [particle masses, etc.] … have no explanations in these string theories – absolutely none!’
– Richard P. Feynman, in Davies & Brown, ‘Superstrings’ 1988, at pages 194-195.
Regarding reality, he said:
‘It always bothers me that, according to the laws as we understand them today, it takes a computing machine an infinite number of logical operations to figure out what goes on in no matter how tiny a region of space, and no matter how tiny a region of time. How can all that be going on in that tiny space? Why should it take an infinite amount of logic to figure out what one tiny piece of spacetime is going to do? So I have often made the hypothesis that ultimately physics will not require a mathematical statement, that in the end the machinery will be revealed, and the laws will turn out to be simple, like the chequer board with all its apparent complexities.’
– R. P. Feynman, The Character of Physical Law, November 1964 Cornell Lectures, broadcast and published in 1965 by BBC, pp. 57-8.
Mathematical physicist Dr Peter Woit at Columbia Univerity mathematics department has written a blog post reviewing a new book about Dirac, the discoverer of the Dirac equation, a relativistic wave equation which lies at the heart of quantum field theory (the Schroedinger equation of quantum mechanics is a good approximation for some low energy physics, but is not valid for relativistic situations, i.e. it doesn’t ensure the field moves with the velocity of light while conserving mass-energy, so it is not a true basis for quantum field descriptions; additionally in quantum field theory but not in quantum mechanics math, pair-production occurs, i.e. “loops” in spacetime on Feynman diagrams, caused by particles and antiparticles briefly gaining energy to free themselves from the normally unobservable ground state of the vacuum of space or Dirac sea, before they annihilate and disappear again, analogous to steam temporarily evaporating from the ocean to create visible clouds which condense into droplets of rain and disappear again, returning back to the sea), http://www.math.columbia.edu/~woit/wordpress/?p=1904 where he writes:
‘As it become harder and harder to get experimental data relevant to the questions we want to answer, the guiding principle of pursuing mathematical beauty becomes more important. It’s quite unfortunate that this kind of pursuit is becoming discredited by string theory, with its claims of seeing “mathematical beauty” when what is really there is mathematical ugliness and scientific failure.’
In 1930 Dirac wrote:
‘The only object of theoretical physics is to calculate results that can be compared with experiment.’
– Paul A. M. Dirac, The Principles of Quantum Mechanics, 1930, page 7.
But he changed slightly in his later years and on 7 May 1963 Dirac actually told Thomas Kuhn during an interview:
‘It is more important to have beauty in one’s equations, than to have them fit experiment.’
– Dirac, ‘The Evolution of the Physicist’s Picture of Nature’, Scientific American, May 1963, 208, 47.
Other guys stuck to their guns:
‘… nature has a simplicity and therefore a great beauty.’
– Richard P. Feynman (The Character of Physical law, p. 173)
‘The beauty in the laws of physics is the fantastic simplicity that they have … What is the ultimate mathematical machinery behind it all? That’s surely the most beautiful of all.’
– John A. Wheeler (quoted by Paul Buckley and F. David Peat, Glimpsing Reality, 1971, p. 60)
‘If nature leads us to mathematical forms of great simplicity and beauty … we cannot help thinking they are true, that they reveal a genuine feature of nature.’
– Werner Heisenberg (http://www.ias.ac.in/jarch/jaa/5/3-11.pdf, page 2 here)
‘A theory is the more impressive the greater the simplicity of its premises is. The more different kinds of things it relates, and the more extended is its area of applicability.’
– Albert Einstein (in Paul Arthur Schilpp’s Albert Einstein: Autobiographical Notes, p. 31)
‘My work always tried to unite the true with the beautiful; but when I had to choose one or the other, I usually chose the beautiful.’
– Hermann Weyl (http://www.ias.ac.in/jarch/jaa/5/3-11.pdf, page 2 here)
Now in a new blog post, ‘The Only Game in Town’, http://www.math.columbia.edu/~woit/wordpress/?p=1917, Dr Woit quotes The First Three Minutes author and Nobel Laureate Steven Weinberg continuing to depressingly hype string theory using the poorest logic imaginable to New Scientist:
“It has the best chance of anything we know to be right,” Weinberg says of string theory. “There’s an old joke about a gambler playing a game of poker,” he adds. “His friend says, ‘Don’t you know this game is crooked, and you are bound to lose?’ The gambler says, ‘Yes, but what can I do, it’s the only game in town.’ We don’t know if we are bound to lose, but even if we suspect we may, it is the only game in town.”
Dr Woit then writes in response to a comment by Dr Thomas S. Love of California State University, asking Woit if he plans to write a sequel to his book Not Even Wrong:
‘Someday I would like to write a technical book on representation theory, QM and QFT, but that project is also a long ways off right now.’
– Peter Woit, May 5, 2009 at 12:48 pm, http://www.math.columbia.edu/~woit/wordpress/?p=1917&cpage=1#comment-48177
Well, I need such a book now, but I’m having to make do with the information currently available in available lecture notes and published quantum field theory textbooks.
It may be interesting to compare the post below to the physically very impoverished situation five years ago when I wrote http://cdsweb.cern.ch/record/706468?ln=en which contains the basic ideas, but with various trivial errors and without the rigorous proofs, predictions, applications and diagrams which have since been developed. Note that Greek symbols in the text display in Internet Explorer with symbol fonts loaded but do not display in Firefox:
1. Masses that attract due to gravity are in fact surrounded by an isotropic distribution of distant receding masses in all directions (clusters of galaxies), so they must exchange gravitons with those distant masses as well as nearby masses (a fact ignored by the flawed mainstream path integral extensions of the Fierz-Pauli argument for gravitons having spin-2 in order for ‘like’ gravitational charges to attract rather than to repel which of course happens with like electric charges; see for instance pages 33-34 of Zee’s 2003 quantum field theory textbook).
2. Because the isotropically distributed distant masses are receding with a cosmological acceleration, they have a radial outward force, which by Newton’s 2nd law is F = ma, and which by Newton’s 3rd law implies an equal inward-directed reaction force, F = -ma.
3. The inward-directed force, from the possibilities known in the Standard Model of particle physics and quantum gravity considerations, is carried by gravitons:

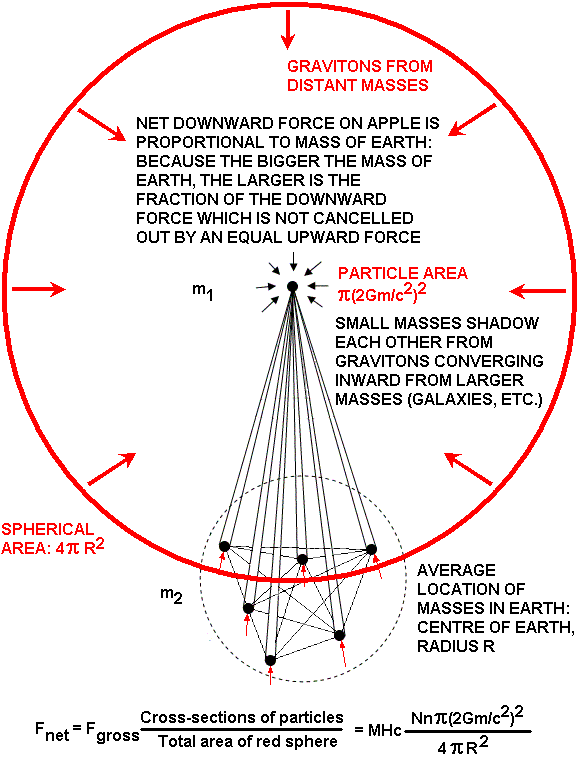
R in the diagram above is the distance to distant receding galaxy clusters of mass m. The distribution of matter around us in the universe can simply be treated as a series of shells of receding mass at progressively larger distances R, and the sum of contributions from all the shells gives the total inward graviton delivered force to masses.
This works for spin-1 gravitons, because:
a. the gravitons coming to you from distant masses (ignored completely by speculative spin-2 graviton hype) are radially converging upon you (not diverging), and
b. the distant masses are immense in size (clusters of galaxies) compared to local masses like the planet earth, the sun or the galaxy.
Consequently, the flux from distant masses is way, way stronger than from nearby masses; so the path integral of all spin-1 gravitons from distant masses reduces to the simple geometry illustrated above and will cause ‘attraction’ or push you down to the earth by shadowing (the repulsion between two nearby masses from spin-1 graviton exchange is trivial compared to the force pushing them together).
 Above: an analogous effect well demonstated experimentally (the experimental data now matches the theory to within 15%) is the Casimir force where the virtual quantum field bosons of the vacuum push two flat metal surfaces together (‘attractive’ force) if they get close enough. The metal plates ‘attract’ because their reflective surfaces exclude virtual photons of wavelengths longer than the separation distance between the plates (the same happens with a waveguide, a metal box like tube which is used to pipe microwaves from the source magnetron to the disc antenna; a waveguide only carries wavelengths smaller than the width and breadth of the metal box!). The exclusion of long wavelengths of virtual radiation from the space between the metal places in the Casimir effect reduces the energy density between the plates compared with that outside, so that – just like external air pressure collapsing a slightly evacuated petrol can in the classic high school demonstration (where you put some water in a can and heat it so the can fills with steam with the cap off, then put the cap on and allow the can to cool so that the water vapour in it condenses, leaving a partial vacuum in the can) – the Casimir force pushes the plates toward one another. From this particular example of a virtual particle mediated force, note that virtual particles do have specific wavelengths! This is essentially important for redshift considerations when force-causing virtual particles (gauge bosons) are exchanged between receding matter in the expanding universe. ‘String theorists’ like Dr Lubos Motl have ignorantly stated to me that virtual particles can’t be redshifted, claiming that they don’t have any particular frequency or wavelength. [Illustration credit: Wikipedia.]
Above: an analogous effect well demonstated experimentally (the experimental data now matches the theory to within 15%) is the Casimir force where the virtual quantum field bosons of the vacuum push two flat metal surfaces together (‘attractive’ force) if they get close enough. The metal plates ‘attract’ because their reflective surfaces exclude virtual photons of wavelengths longer than the separation distance between the plates (the same happens with a waveguide, a metal box like tube which is used to pipe microwaves from the source magnetron to the disc antenna; a waveguide only carries wavelengths smaller than the width and breadth of the metal box!). The exclusion of long wavelengths of virtual radiation from the space between the metal places in the Casimir effect reduces the energy density between the plates compared with that outside, so that – just like external air pressure collapsing a slightly evacuated petrol can in the classic high school demonstration (where you put some water in a can and heat it so the can fills with steam with the cap off, then put the cap on and allow the can to cool so that the water vapour in it condenses, leaving a partial vacuum in the can) – the Casimir force pushes the plates toward one another. From this particular example of a virtual particle mediated force, note that virtual particles do have specific wavelengths! This is essentially important for redshift considerations when force-causing virtual particles (gauge bosons) are exchanged between receding matter in the expanding universe. ‘String theorists’ like Dr Lubos Motl have ignorantly stated to me that virtual particles can’t be redshifted, claiming that they don’t have any particular frequency or wavelength. [Illustration credit: Wikipedia.]
 Above: incorporation of quantum gravity, mass (without Higgs field) and charged electromagnetic gauge bosons into the Standard Model. Normally U(1) is weak hypercharge. The key point about the new model is that (as we will prove in detail below) the Yang-Mills equation applies to electromagnetism if the gauge bosons are charged, but is restricted to Maxwellian force interactions for massless charged gauge bosons due to the magnetic self-inductance of such massive charges. Magnetic self-inductance requires that charged massless gauge bosons must simultaneously be transferring equal charge from charge A to charge B as from B to A. In other words, only an exact equilibrium of exchanged charge per second in both directions between two charges is permitted, which prevents the Yang-Mills equation from changing the charge of a fermion: it is restricted to Maxwellian field behaviour and can only change the motion (kinetic energy) of a fermion. In other words, it can deliver net energy but not net charge. So it prevents the massless charged gauge bosons from transferring any net charge (they can only propagate in equal measure in both directions between charges so that the curling magnetic fields cancel, which is any equilibrium which can deliver field energy but cannot deliver field charge). Therefore, the Yang-Mills equation reduces for massless charged gauge bosons to the Maxwell equations, as we will prove later on in this blog post. The advantages of this model are many for the Standard Model, because it means that U(1) now does the job of quantum gravity and the ‘Higgs mechanism’, which are both speculative (untested) additions to the Standard Model, but does it in a better way, leading to predictions that can be checked experimentally.
Above: incorporation of quantum gravity, mass (without Higgs field) and charged electromagnetic gauge bosons into the Standard Model. Normally U(1) is weak hypercharge. The key point about the new model is that (as we will prove in detail below) the Yang-Mills equation applies to electromagnetism if the gauge bosons are charged, but is restricted to Maxwellian force interactions for massless charged gauge bosons due to the magnetic self-inductance of such massive charges. Magnetic self-inductance requires that charged massless gauge bosons must simultaneously be transferring equal charge from charge A to charge B as from B to A. In other words, only an exact equilibrium of exchanged charge per second in both directions between two charges is permitted, which prevents the Yang-Mills equation from changing the charge of a fermion: it is restricted to Maxwellian field behaviour and can only change the motion (kinetic energy) of a fermion. In other words, it can deliver net energy but not net charge. So it prevents the massless charged gauge bosons from transferring any net charge (they can only propagate in equal measure in both directions between charges so that the curling magnetic fields cancel, which is any equilibrium which can deliver field energy but cannot deliver field charge). Therefore, the Yang-Mills equation reduces for massless charged gauge bosons to the Maxwell equations, as we will prove later on in this blog post. The advantages of this model are many for the Standard Model, because it means that U(1) now does the job of quantum gravity and the ‘Higgs mechanism’, which are both speculative (untested) additions to the Standard Model, but does it in a better way, leading to predictions that can be checked experimentally.
In the case of electromagnetism, like charges repel due to spin-1 virtual photon exchange, because the distant matter in the universe is electrically neutral (equal amounts of charge of positive and negative sign at great distances cancel). This is not the case for quantum gravity, because the distant masses have the same gravitational charge sign, say positive, as nearby masses (there is only one observed sign for all gravitational charges!). Hence, nearby like gravitational charges are pushed together by gravitons from distant masses, while nearby like electric charges are pushed apart by exchange spin-1 photons with one another but not significantly by virtual photon exchanges with distant matter (due to that matter being electrically neutral).
The new model has particular advantages to electromagnetism and leads to quantitative predictions of the masses of particles, and predicting the force coupling strengths for the various interactions. E.g., as shown in previous posts, a random walk of charged electromagnetic gauge bosons between similar charges randomly scattered around the universe gives a path integral with a total force coupling that is 1040 times that from quantum gravity, and so it predicts quantitatively how electromagnetism is stronger than gravity.
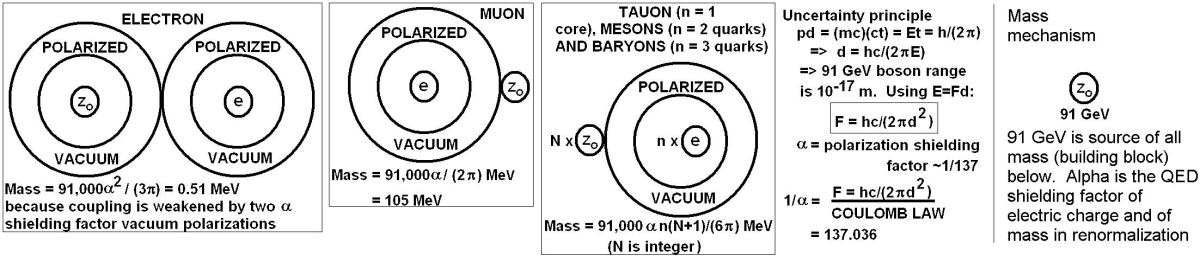
Above: If a discrete number of fixed-mass gravitational charges clump around each fermion core, ‘miring it’ like treacle, you can predict all lepton and hadron inertial and gravitational masses. The gravitational charges have inertia because they are exchanging gravitons with all other masses around the universe, which physically holds them where they are (if they move, they encounter extra pressure from graviton exchange in the direction of their motion, which causes contraction, requiring energy; hence resistance to acceleration, which is just Newton’s 1st law, inertia). The illustration of a miring particle mass model shows a discrete number of 91 GeV mass particles surrounding the IR cutoff outer edge of the polarized vacuum around a fundamental particle core, giving mass. A PDF table comparing crude model mass estimates to observed masses of particles is linked here. There is evidence for the quantization of mass from the way the mathematics work for spin-1 quantum gravity. If you treat two masses being pushed together by spin-1 graviton exchanges with the isotropically distributed mass of the universe accelerating radially away from them (viewed in their reference frame), you get the expected correct a prediction of gravity as illustrated here. But if you do the same spin-1 quantum gravity analysis but only consider one mass and try to work out the acceleration field around it, as illustrated here, you get (using the empirically defensible black hole event horizon radius to calculate the graviton scatter cross-section) a prediction that gravitational force is proportional to mass2, which suggests all particles masses are built up from a single fixed size building block of mass. The identification of the number of mass particles to each fermion (fundamental particle) in the illustration and in the table here is by the analogy of nuclear magic numbers: in the shell model of the nucleus the exceptional stability of nuclei containing 2, 8, 20, 50 or 82 protons or 2, 8, 20, 50, 82 or 126 neutrons (or both), which are called ‘magic numbers’, is explained by the fact that these numbers represent successive completed (closed) shells of nucleons, by analogy to the shell structure of electrons in the atom. (Each nucleon has a set of four quantum numbers and obeys the exclusion principle in the nuclear structure, like electrons in the atom; the difference being that for orbital electrons there is generally no interaction of the orbital angular momentum and the spin angular momentum, whereas such an interaction does occur for nucleons in the nucleus.) Geometric factors like twice Pi appear to be obtained from spin considerations, as discussed in earlier blog posts, and they are common in quantum field theory. E.g., Schwinger’s correction factor for Dirac’s magnetic moment of the electron is 1 + (alpha)/(2*Pi).
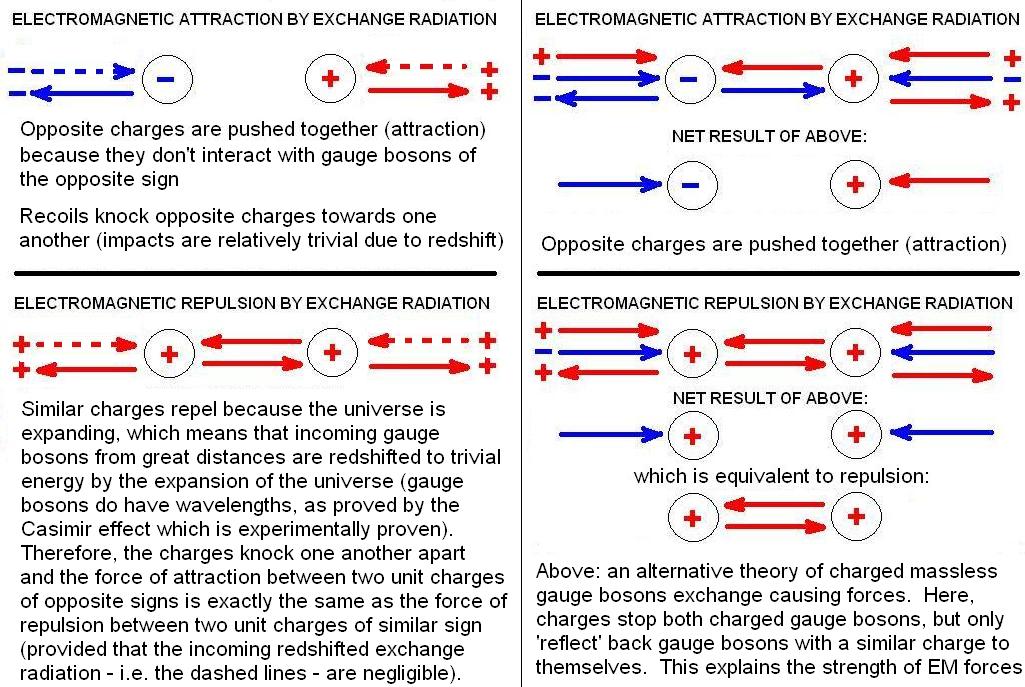
Above: the mechanism for electromagnetic forces explains physically how those force interactions occur by the exchange of gauge bosons (without invoking the magical ‘4-polarization photon’), allowing the understanding of fields and resolving anomalies in electromagnetism. The first evidence that the gauge bosons of electromagnetism are charged was the transmission line of electricity: both conductors propagate a charged field at the velocity of light for the surrounding insulator, as demonstrated on the blog page here. So in addition to the new quantum gravity model’s ability to predict masses of fundamental particles and the coupling constant for gravity, it also deals with electromagnetism properly, showing why its force strength differs from gravity so much (electromagnetism theoretically involves a random walk between all charges in the universe, which makes it stronger than gravity by the square root of the number of fermions, 1080/2 = 1040).
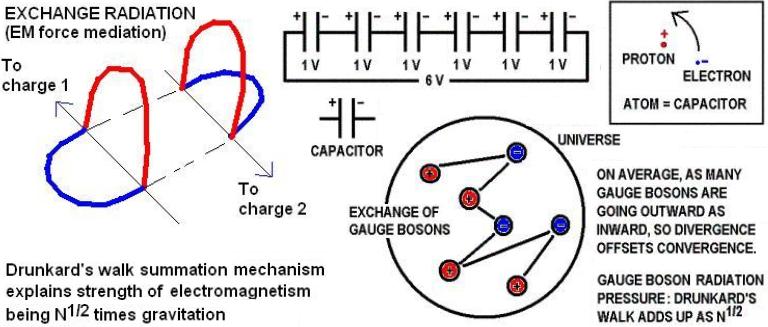
Above: a random walk of charged massless electromagnetic gauge bosons between N = 1080 fermions in the universe would create a force that adds up to the square root of that number (N1/2 = 1040) multiplied by the force between just two particles, explaining why the force we calculate for quantum gravity between just two particles is smaller by a factor of 1040 than the force of electromagnetism! In other words, electromagnetism is much stronger than gravity because its path integral includes addictive contributions from all the charges in the universe (albeit with gross inefficiency due to the vector directions not adding up coherently, i.e. the random walk summation gives an effective sum of only 1040 not 1080 times gravity), whereas gravity carried by uncharged spin-1 gauge bosons does not involve force enhancing contributions from all the mass in the universe but just the line-of-sight shadowing of one mass by another.

Above: photons, real and virtual, compared to Maxwell’s photon illustration. The Maxwell model photon is always drawn as an electric and magnetic ‘fields’ both at right angles (orthagonal) to the direction of propagation; however this causes confusion because people assume that the ‘fields’ are directions, whereas they are actually field strengths. When you plot a graph of a field strength versus distance, the field strength doesn’t indicate distance. It is true that a transverse wave like a photon has a transverse extent, but this is not indicated by a plot of E-field strength and B-field strength versus propagation distance! People get confused and think it is a three dimensional plot of a photon, when it is just a 1-dimensional plot and merely indicates how the magnetic field strength and electric field strength vary in the direction of propagation! Maxwell’s theory is empty when you recognise this, because you are left with a 1-dimensional photon, not a truly transverse photon as observed. So we illustrate above how photons really propagate, using hard facts from the study of the propagation of light velocity logic signals by Heaviside and Catt, with corrections for their errors. The key thing is that massless charges won’t propagate in a single direction only, because the magnetic fields it produces cause self-inductance which prevent motion. Massive charges overcome this by radiating electromagnetic waves as they accelerate, but massless charges will only propagate if there is an equal amount of charge flowing in the opposite direction at the same time so cancel out their magnetic field (because the magnetic fields curl around the direction of propagation, they cancel in this situation if the charges are similar). So we can deduce the mechanism of propagation of real photons and virtual (exchange) gauge bosons, and the mechanism is compatible with path integrals, the double slit diffraction experiment with single photons (the transverse extent of the photon must be bigger than the distance between slits for an interference pattern), etc.
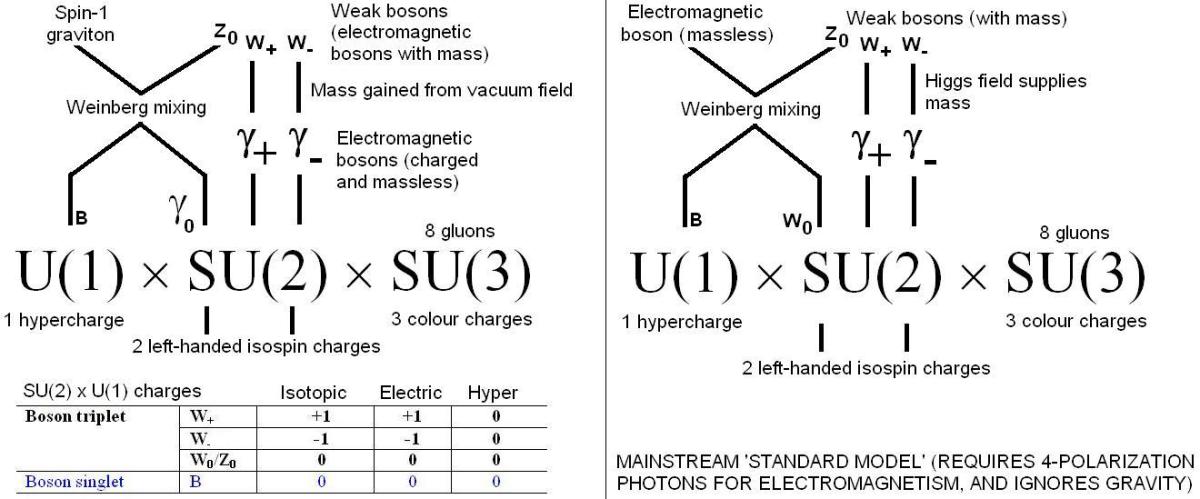
Above: the incorporation of U(1) charge as mass (gravitational vacuum charge is quantized and always have identical mass to the Z0 as already shown) and mixed neutral U(1) x SU(2) gauge bosons as quantum spin-1 gravitons into the empirical, heuristically developed Standard Model of particle physics. The new model is illustrated on the left and the old Standard Model is illustrated on the right. The SU(3) colour charge theory for strong interactions and quark triplets (baryons) is totally unaltered. The electroweak U(1) x SU(2) symmetry is radically altered in interpretation but not in mathematical structure! The difference is that the massless charged SU(2) gauge bosons are assumed to all acquire mass in low energy physics low energy from some kind of unobserved ‘Higgs field’ (there are several models with differing numbers of Higgs bosons). This means that in the Standard Model, a ‘special’ 4-polarization photon mediates the electromagnetic interactions (requiring 4 polarizations so it mediate both positive and negative force fields around positive and negative charges, not merely the 2 polarizations we observe with photons!).
Correcting the Standard Model so that it deals with electromagnetism correctly and contains gravity simply requires the replacement of the Higgs field with one that only couples to one spin handedness of the electrically charged SU(2) bosons, giving them mass. The other handedness of electrically charged SU(2) bosons remain massless even at low energy and mediate electromagnetic interactions!
To understand how this works, notice that the weak force isospin charges of the weak bosons, such as W– and W+, is identical to their electric charges! Isospin is acquired when an electrically charged massless gauge boson (with no isotopic charge) acquires mass from the vacuum. The key difference between isotopic spin and electric charge is the massiveness of the gauge bosons, which alone determines whether the field obeys the Yang-Mills equation (where particle charge can be altered by the field) or the Maxwell equations (where a particle’s charge cannot be affected by the field). This is a result of magnetic self-inductance created by the motion of a charge:
(1) A massless electric charge can’t propagate in one direction by itself, because such motion of massless charge would cause infinite magnetic self-inductance that prevents motion. (Massless radiations can’t be accelerated because they only travel at the velocity of light, so unlike massive charged radiations, they cannot compensate for magnetic effects by radiating energy while being accelerated.) Therefore massless charged radiation cannot propagate to deliver charge to a particle! Massless charged radiation can only ever behave as ‘exchange radiation’, whereby there is an equal flux of charged massless radiation from charge A to B and simultaneously back from B to A, so that the opposite magnetic curls of each opposite-directed flux of exchange radiation oppose one another and cancel out, preventing the problem of magnetic self-inductance. In this situation, the charge of fermions remains constant and cannot ever vary, because the charge each fermion loses per second is equal to the amount of charge delivered to it by the equilibrium of exchange radiation. In other words, the energy delivered by the charged massless gauge bosons can vary (if charges move apart for instance, it can be redshifted), but the electric charge delivered is always in equilibrium with that emitted each second. Hence, the Yang-Mills equation is severely constrained in the case of electromagnetism and reduces to the Maxwell theory, as observed.
(2) Massive charged gauge boson can propagate by themselves in one direction because they can accelerate due to having mass which makes them move slower than light (if they were massless this would not be true, because a massless gauge boson goes at light velocity and cannot be accelerated to any higher velocity): this acceleration permits the charged massive particle to get around infinite magnetic self-inductance by radiating electromagnetic waves while accelerating. Therefore, massive charged gauge bosons can carry a net charge and can affect the charge of the fermions they interact with, which is why they obey the Yang-Mills equation not Maxwell’s.
Electromagnetism is described by SU(2) isospin with massless charged positive and negative gauge bosons
The usual argument against massless charged radiation propagating is infinite self-inductance, but as discussed in the blog page here this doesn’t apply to virtual (gauge boson) exchange radiations, because the curls of magnetic fields around the portion of the radiation going from charge A to charge B is exactly cancelled out by the magnetic field curls from the radiation going the other way, from charge B to charge A. Hence, massless charged gauge bosons can propagate in space, provided they are being exchanged simultaneously in both directions between electric charges, and not just from one charge to another without a return current.
You really need electrically charged gauge bosons to describe electromagnetism, because the electric field between two electrons is different in nature to that between two positrons: so you can’t describe this difference by postulating that both fields are mediated by the same neutral virtual photons, unless you grant the 2 additional polarizations of the virtual photon (the ordinary photon has only 2 polarizations, while the virtual photon must have 4) to be electric charge!
The virtual photon mediated between two electrons is negatively charged and that mediated between two positrons (or two protons) is positively charged. Only like charges can exchange virtual photons with one another, so two similar charges exchange virtual photons and are pushed apart, while opposite electric charges shield one another and are pushed together by a random-walk of charged virtual photons between the randomly distributed similar charges around the universe as explained in a previous post.
What is particularly neat having electrically charged electromagnetic virtual photons is that it automatically requires a SU(2) Yang-Mills theory! The mainstream U(1) Maxwellian electromagnetic gauge theory makes a change in the electromagnetic field induce a phase shift in the wave function of a charged particle, not in the electric charge of the particle! But with charged gauge bosons instead of neutral gauge bosons, the bosonic field is able to change the charge of a fermion just as the SU(2) charged weak bosons are able to change the isospin charges of fermions.
We don’t see electromagnetic fields changing the electric charge of fermions normally because fermions radiate as much electric charge per second as they receive, from other charges, thereby maintaining an equilibrium. However, the electric field of a fermion is affected by its state of motion relative to an observer, when the electric field line distribution appears to make the electron “flatten” in the direction of motion due to Lorentz contraction at relativistic velocities. To summarize:
U(1) electromagnetism: is described by Maxwellian equations. The field is uncharged and so cannot carry charge to or from fermions. Changes in the field can only produce phase shifts in the wavefunction of a charged particle, such as acceleration of charges, and can never change the charge of a charged particle.
SU(2) electromagnetism (two charged massless gauge bosons): is described by the Yang-Mills equation because the field is electrically charged and can change not just the phase of the wavefunction of a charged particle to accelerate a charge, but can also in principle (although not in practice) change the electric charge of a fermion. This simplifies the Standard Model because SU(2) with two massive charged gauge bosons is already needed, and it naturally predicts (in the absence of a Higgs field without a chiral discrimination for left-handed spinors) the existence of massless uncharged versions of the these massive charged gauge bosons which were observed at CERN in 1983.
The Yang-Mills equation is used for any bosonic field which carries a charge and can therefore (in principle) change the charge of a fermion. The weak force SU(2) charge is isospin and the electrically charged massive weak charge gauge bosons carry an isospin charge which is IDENTICAL to the electric charge, while the massive neutral weak boson has zero electric charge and zero isospin charge. The Yang-Mills equation is:
dFmn/dxn + 2e(An x Fmn) + Jm = 0
which is similar to Maxwell’s equations (Fmn is the field strength and Jm is the current), apart from the second term, 2e(An x Fmn), which describes the effect of the charged field upon itself (e is charge and An is the field potential). The term 2e(An x Fmn) doesn’t appear in Maxwell’s equations for two reasons:
(1) an exact symmetry between the rate of emission and reception of charged massless electromagnetic gauge bosons is forced by the fact that charged massless gauge bosons can only propagate in the vacuum where there is an equal return current coming from the other direction (otherwise they can’t propagate, because charged massless radiation has infinite self-inductance due to the magnetic field produced, which is only cancelled out if there is an identical return current of charged gauge bosons, i.e. a perfect equilibrium or symmetry between the rates of emission and reception of charged massless gauge bosons by fermionic charges). This prevents fermionic charges from increasing or decreasing, because the rate of gain and rate of loss of charge per second is always the same.
(2) the symmetry between the number of positive and negative charges in the universe keeps electromagnetic field strengths low normally, so the self-interaction of the charge of the field with itself is minimal.
These two symmetries act together to prevents the Yang-Mills 2e(An x Fmn) term from having any observable effect in laboratory electromagnetism, which is why the mainstream empirical Maxwellian model works as a good approximation, despite being incorrect at a more fundamental physical level of understanding.
Quantum gravity is supposed to be similar to a Yang-Mills theory in regards to the fact that the energy of the gravitational field is supposed (in general relativity, which ignores vital quantum effects the mass-giving “Higgs field” or whatever and its interaction with gravitons) to be a source for gravity itself. In other words, like a Yang-Mills field, the gravitational field is supposed to generate a gravitational field simply by virtue of its energy, and therefore should interact with itself. If this simplistic idea from general relativity is true, then according to the theory presented on this blog page, the massless electrically neutral gauge boson of SU(2) is the spin-1 graviton. However, the structure of the Standard Model implies that some field is needed to provide mass even if the mainstream Higgs mechanism for electroweak symmetry breaking is wrong.
Therefore, the massless electrically neutral (photon-like) gauge boson of SU(2) may not be the graviton, but is instead an intermediary gauge boson which interacts in a simple way with massive (gravitational charge) particles in the vacuum: these massive (gravitational charge) particles may be described by the simple Abelian symmetry U(1). So U(1) then describes quantum gravity: it has one charge (mass) and one gauge boson (spin-1 graviton).
‘Yet there are new things to discover, if we have the courage and dedication (and money!) to press onwards. Our dream is nothing else than the disproof of the standard model and its replacement by a new and better theory. We continue, as we have always done, to search for a deeper understanding of nature’s mystery: to learn what matter is, how it behaves at the most fundamental level, and how the laws we discover can explain the birth of the universe in the primordial big bang.’ – Sheldon L. Glashow, The Charm of Physics, American Institute of Physics, New York, 1991. (Quoted by E. Harrison, Cosmology, Cambridge University press, London, 2nd ed., 2000, p. 428.)
Conventionally U(1) represents weak hypercharge and SU(2) the weak interaction, with the unobserved B gauge boson of U(1) ‘mixing’ (according to the Glashow/Weinberg mixing angle) with the W0 unobserved gauge boson of SU(2) to produce the observed electromagnetic photon, and the observed weak neutral current gauge boson, the Z0. (It’s not specified in the Standard Model whether this mixing is supposed to occur before or after the weak gauge bosons have actually acquired mass from the speculative Higgs field. The Higgs field is a misnomer since there isn’t one specific theory but various speculations, including contradictory theories with differing numbers of ‘Higgs bosons’, none of which have been observed. Woit mentions in Not Even Wrong that since Weinberg put a Higgs’s mechanism into the electroweak theory in 1967, the Higgs theory is called ‘Weinberg’s toilet’ by Glashow – Woit’s undergraduate adviser – because, although a mass-giving field is needed to give mass to weak bosons and thus break electroweak symmetry into separate electromagnetic and weak forces at low energy, Higgs’ theories stink.)
In the empirical model we will describe in this post, U(1) is still weak hypercharge but SU(2) without mass is electromagnetism (with charged massless gauge bosons, positive for positive electric fields and negative for negative electric fields) and left-handed isospin charge (forming quark doublets, mesons). The Glashow/Weinberg mixing remains, but the massless electrically neutral product is the graviton, an unobservably high-energy photon whose wavelength is so small that it only interacts with the tiny black hole-sized cores of the gravitational charges (masses) of fundamental particles. This has the advantage of making U(1) x SU(2) x SU(3) a theory of all interactions, without changing the experimentally-confirmed mathematical structure significantly (we will show below how the Yang-Mills equation reduces to the Maxwell equations for charged massless gauge bosons). The addition of mass to the half of the electromagnetic gauge bosons gives them their left-handed weak isospin charge so they interact only with left-handed spinors. The other features of the weak interaction (apart from just acting on left-handed spinors) such as the weak interaction strength and the short range, are also due to the massiveness of the weak gauge bosons.
Beta radioactivity, controlled by the weak force, is the process whereby neutrons decay into protons, electrons and antineutrinos by a downquark decaying into an upquark by emitting a W– weak boson which they decays into an electron and an antineutrino.
This weak interaction is asymmetric due to the massive gauge bosons: free protons can’t ever decay by an upquark transforming into a downquark through emitting a W+ weak boson which then decays into a neutrino and a positron. The reason? Violation of mass-energy conservation! The decay of free protons into neutrons is banned because neutrons are heavier than protons, and mass-energy is conserved. (Protons bound in nuclei get extra effective mass from the binding energy of the strong force field in the nucleus, so in some cases – such as radioactive carbon-11 which is used in PET scanners – protons decay into neutrons by emitting a positive weak gauge boson which decays into a positron and a neutrino.) The left-handedness of the weak interaction is produced by the coupling of the gauge bosons to massive vacuum charges. The short-range, strength and the left-handedness of weak interactions are all due to the effect of mass on electromagnetic gauge bosons and charges. Mass limits the range and strength of the weak interaction and it prevents right-handed spinors undergoing weak interactions. The whole point about electroweak theory is that the electromagnetic and weak interactions are identical in strength and nature apart from the effect that the weak gauge bosons are massive. Whereas the electromagnetic force charge for beta decay is {alpha} ~ 1/137.036…, the corresponding weak force charge for low energies (proton-sized distances) is {alpha}*(Mproton/MW)2, so that it depends on the square of the ratio of the mass of the proton (the decay product in beta decay) to the mass of the weak gauge boson involved, MW. Since Mproton ~ 1 GeV and MW ~ 80 GeV, the low-energy weak force charge is on the order of 1/802 of the electromagnetic charge, alpha. It is the fact that the weak interaction involves massive virtual photons, with over 80 times the mass of the decay products (!), which cause it to be so much weaker than electromagnetism at low energies (nuclear-sized distances). Neglecting the effects of mass on the interaction strength and range of the weak force, it is the same thing as electromagnetism. At very high energies exceeding 100 GeV (short distances, less than 10-18 metre), the massive weak gauge bosons can be exchanged without the distance being an issue, and the weak force is then similar in strength to the electromagnetic force! The weak and strong forces can only act over a maximum distance of about 1 Fermi (10-15 metre) due to the limited range of the gauge bosons (massive W’s for the weak interaction, and pions for the longest-range residual component of the strong colour force).
Electromagnetic and strong forces conserve the number of interacting fermions, so that the number of fermion reactants is the same as the number of fermion products, but the weak force allows the number of fermion products to differ from the number of fermion reactants. The weak force involves neutrinos which have weak charges, little mass and no electromagnetic or strong charge, so they are weakly interacting (very penetrating).
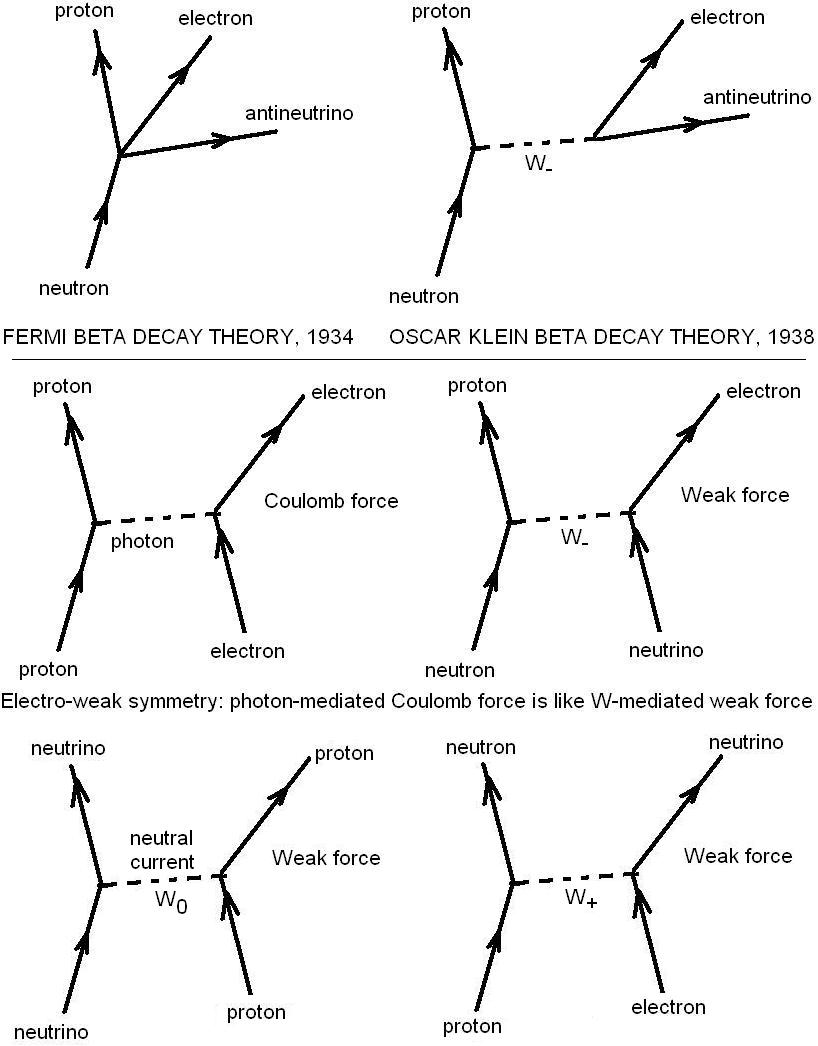 Above: beta decay is controlled by the weak force which is similar to the electromagnetic interaction (on a Feynman diagram, an ingoing neutrino is equivalent to having an antineutrino as an interaction product). In place of electromagnetic photons mediating particle interaction, there are three weak gauge bosons. If these weak gauge bosons were massless, the strength of the weak interaction would be the same as the electromagnetic interaction. However, the weak gauge bosons are massive, and that makes the weak interaction much weaker than electromagnetism at low energies (i.e. relatively big, nucleon-sized distances). This is because the massive virtual weak gauge bosons are short-ranged dut to their massiveness (they suffer rapid attenuation with distance in the quantum field vacuum), so the weak boson interaction rate drops sharply with increasing distance. Hence, by analogy to Yukawa’s famous 1935 theoretical prediction of the pion mass using the experimentally known radius of pion-mediated nuclear interactions, it was possible to predict that the mass of the weak gauge bosons using Glashow’s theory of weak interactions and the experimentally known weak interaction strength, giving was 82 (W– and W+) and 92 GeV (Z0), predictions which were closely confirmed by the 27-km diameter LEP (large electron-positron) collider experiments announced at CERN on 21 January 1983. (The masses are now established to be 80.4 and 91.2 GeV respectively.) Neutral currents due to exchange of electrically neutral massive W0 or Z0 (as it is known after it has undergone Weinberg-Glashow mixing with the photon in electroweak theory) gauge bosons had already been confirmed experimentally in 1973, leading to the award of the 1979 Nobel Prize to Glashow, Salam and Weinberg for the SU(2) weak gauge boson theory (Glashow’s work of 1961 had been extended by Weinberg and Salam in 1967). (No Nobel Prize has been awarded for the entire electroweak theory because nobody has detected the speculative Higgs field boson(s) postulated to give mass and thus electroweak symmetry breaking in the mainstream electroweak theory.) One neutral current interaction is illustrated above. However, other Z0 neutral currents exist and are very similar to electromagnetic interactions, e.g. the Z0 can mediate electron scattering, although at low energies this process will be trivial in comparison to electromagnetic (Coulomb) scattering on account of the mass of the Z0 which makes the massive neutral current interaction weak and trivial compared to electromagnetism at low energies (i.e. large distances).
Above: beta decay is controlled by the weak force which is similar to the electromagnetic interaction (on a Feynman diagram, an ingoing neutrino is equivalent to having an antineutrino as an interaction product). In place of electromagnetic photons mediating particle interaction, there are three weak gauge bosons. If these weak gauge bosons were massless, the strength of the weak interaction would be the same as the electromagnetic interaction. However, the weak gauge bosons are massive, and that makes the weak interaction much weaker than electromagnetism at low energies (i.e. relatively big, nucleon-sized distances). This is because the massive virtual weak gauge bosons are short-ranged dut to their massiveness (they suffer rapid attenuation with distance in the quantum field vacuum), so the weak boson interaction rate drops sharply with increasing distance. Hence, by analogy to Yukawa’s famous 1935 theoretical prediction of the pion mass using the experimentally known radius of pion-mediated nuclear interactions, it was possible to predict that the mass of the weak gauge bosons using Glashow’s theory of weak interactions and the experimentally known weak interaction strength, giving was 82 (W– and W+) and 92 GeV (Z0), predictions which were closely confirmed by the 27-km diameter LEP (large electron-positron) collider experiments announced at CERN on 21 January 1983. (The masses are now established to be 80.4 and 91.2 GeV respectively.) Neutral currents due to exchange of electrically neutral massive W0 or Z0 (as it is known after it has undergone Weinberg-Glashow mixing with the photon in electroweak theory) gauge bosons had already been confirmed experimentally in 1973, leading to the award of the 1979 Nobel Prize to Glashow, Salam and Weinberg for the SU(2) weak gauge boson theory (Glashow’s work of 1961 had been extended by Weinberg and Salam in 1967). (No Nobel Prize has been awarded for the entire electroweak theory because nobody has detected the speculative Higgs field boson(s) postulated to give mass and thus electroweak symmetry breaking in the mainstream electroweak theory.) One neutral current interaction is illustrated above. However, other Z0 neutral currents exist and are very similar to electromagnetic interactions, e.g. the Z0 can mediate electron scattering, although at low energies this process will be trivial in comparison to electromagnetic (Coulomb) scattering on account of the mass of the Z0 which makes the massive neutral current interaction weak and trivial compared to electromagnetism at low energies (i.e. large distances).
How this gravity mechanism updates the Standard Model of particle physics
‘The electron and antineutrino [both emitted in beta decay of neutron to proton as argued by Pauli in 1930 from energy conservation using the experimental data on beta energy spectra; the mean beta energy is only 30% of the energy lost in beta decay so 70% on average must be in antineutrinos] each have a spin 1/2 and so their combination can have spin total 0 or 1. The photon, by contrast, has spin 1. By analogy with electromagnetism, Fermi had (correctly) supposed that only the spin 1 combination emerged in the weak decay. To further the analogy, in 1938, Oscar Klein suggested that a spin 1 particle (‘W boson’) mediated the decay, this boson playing a role in weak interactions like that of the photon in the electromagnetic case [electron-proton scattering is mediated by virtual photons, and is analogous to the W-mediated ‘scattering’ interaction between a neutron and a neutrino (not antineutrino) that results in a proton and an electron/beta particle; since an incoming (reactant) neutrino has the same effect on a reaction as a released (resultant) antineutrino, this process W-mediated scattering is equivalent to the beta decay of a neutron].
‘In 1957, Julian Schwinger extended these ideas and attempted to build a unified model of weak and electromagnetic forces by taking Klein’s model and exploiting an analogy between it and Yukawa’s model of nuclear forces [where pion exchange between nucleons causes the attractive component of the strong interaction, binding the nucleons into the nucleus against the repulsive electric force between protons]. As the pion+, pion–, and pion0 are exchanged between interacting particles in Yukawa’s model of the nuclear force, so might the W+, W–, and [W0] photon be in the weak and electromagnetic forces.
‘However, the analogy is not perfect … the weak and electromagnetic forces are very sensitive to electrical charge: the forces mediated by W+ and W– appear to be more feeble than the electromagnetic force.’ – Professor Frank Close, The New Cosmic Onion, Taylor and Francis, New York, 2007, pp. 108-9.
The Yang-Mills SU(2) gauge theory of 1954 was first (incorrectly but interestingly) applied to weak interactions by Schwinger and Glashow in 1956, as Glashow explains in his Nobel prize award lecture:
‘Schwinger, as early as 1956, believed that the weak and electromagnetic interactions should be combined into a gauge theory. The charged massive vector intermediary and the massless photon were to be the gauge mesons. As his student, I accepted his faith. … We used the original SU(2) gauge interaction of Yang and Mills. Things had to be arranged so that the charged current, but not the neutral (electromagnetic) current, would violate parity and strangeness. Such a theory is technically possible to construct, but it is both ugly and experimentally false [H. Georgi and S. L. Glashow, Physical Review Letters, 28, 1494 (1972)]. We know now that neutral currents do exist and that the electroweak gauge group must be larger than SU(2).
‘Another electroweak synthesis without neutral currents was put forward by Salam and Ward in 1959. Again, they failed to see how to incorporate the experimental fact of parity violation. Incidentally, in a continuation of their work in 1961, they suggested a gauge theory of strong, weak and electromagnetic interactions based on the local symmetry group SU(2) x SU(2) [A. Salam and J. Ward, Nuovo Cimento, 19, 165 (1961)]. This was a remarkable portent of the SU(3) x SU(2) x U(1) model which is accepted today.
‘We come to my own work done in Copenhagen in 1960, and done independently by Salam and Ward. We finally saw that a gauge group larger than SU(2) was necessary to describe the electroweak interactions. Salam and Ward were motivated by the compelling beauty of gauge theory. I thought I saw a way to a renormalizable scheme. I was led to SU(2) x U(1) by analogy with the appropriate isospin-hypercharge group which characterizes strong interactions. In this model there were two electrically neutral intermediaries: the massless photon and a massive neutral vector meson which I called B but which is now known as Z. The weak mixing angle determined to what linear combination of SU(2) x U(1) generators B would correspond. The precise form of the predicted neutral-current interaction has been verified by recent experimental data. …’
Glashow in 1961 published an SU(2) model which had three weak gauge bosons, the neutral one of which could mix with the photon of electromagnetism to produce the observed neutral gauge bosons of electroweak interactions. (For some reason, Glashow’s weak mixing angle is now called Weinberg’s mixing angle.) Glashow’s theory predicted massless weak gauge bosons, not massive ones.
For this reason, a mass-giving field suggested by Peter Higgs in 1964 was incorporated into Glashow’s model by Weinberg as a mass-giving and symmetry-breaking mechanism (Woit points out in his book Not Even Wrong that this Higgs field is known as ‘Weinberg’s toilet’ because it was a vauge theory which could exist in several forms with varying numbers of speculative ‘Higgs bosons’, and it couldn’t predict the exact mass of a Higgs boson).
I’ve explained in a previous post, here, where we depart from Glashow’s argument: Glashow and Schwinger in 1956 investigated SU(2) using for the 3 gauge bosons 2 massive weak gauge bosons and 1 uncharged electromagnetic massless gauge boson. This theory failed to include the massive uncharged Z gauge boson that produces neutral currents when exchanged. Because this specific SU(2) electro-weak theory is wrong, Glashow claimed that SU(2) is not big enough to include both weak and electromagnetic interactions!
However, this is an arm-waving dismissal and ignores a vital and obvious fact: SU(2) has 3 vector bosons but you need to supply mass to them by an external field (the Standard Model does this with some kind of speculative Higgs field, so far unverified by experiment). Without that (speculative) field, they are massless. So in effect SU(2) produces not 3 but 6 possible different gauge bosons: 3 massless gauge bosons with long range, and 3 massive ones with short range which describe the left-handed weak interaction.
It is purely the assumed nature of the unobserved, speculative Higgs field which tries to get rid of the 3 massless versions of the weak field quanta! If you replace the unobserved Higgs mass mechanism with another mass mechanism which makes checkable predictions about particle masses, you then arrive at an SU(2) symmetry with in effect 2 versions (massive and massless) of the 3 gauge bosons of SU(2), and the massless versions of those will give rise to long-ranged gravitational and electromagnetic interactions. This reduces the Standard Model from U(1) x SU(2) x SU(3) to just SU(2) x SU(3), while incorporating gravity as the massless uncharged gauge boson of SU(2). I found the idea that that chiral symmetry features of the weak interaction connects with electroweak symmetry breaking in Dr Peter Woit’s 21 March 2004 ‘Not Even Wrong’ blog posting The Holy Grail of Physics:
‘An idea I’ve always found appealing is that this spontaneous gauge symmetry breaking is somehow related to the other mysterious aspect of electroweak gauge symmetry: its chiral nature. SU(2) gauge fields couple only to left-handed spinors, not right-handed ones. In the standard view of the symmetries of nature, this is very weird. The SU(2) gauge symmetry is supposed to be a purely internal symmetry, having nothing to do with space-time symmetries, but left and right-handed spinors are distinguished purely by their behavior under a space-time symmetry, Lorentz symmetry. So SU(2) gauge symmetry is not only spontaneously broken, but also somehow knows about the subtle spin geometry of space-time. Surely there’s a connection here… So, this is my candidate for the Holy Grail of Physics, together with a guess as to which direction to go looking for it.’
As discussed in previous blog posts, e.g. this, the fact that the weak force is left-handed (affects only particles with left-handed spin) arises from the coupling of massive bosons in the vacuum to the weak gauge bosons: this coupling of massive bosons to the weak gauge bosons prevents them from interacting with particles with right-handed spin. The massless versions of the 3 SU(2) gauge bosons don’t get this spinor discrimination because they don’t couple with massive vacuum bosons, so the massless 3 SU(2) gauge bosons (which give us electromagnetism and gravity) are not limited to interacting with just one handedness of particles in the universe, but equally affect left- and right-handed particles. Further research on this topic is a underway. The ‘photon’ of U(1) is mixed via the Weinberg mixing angle in the standard model with the electrically neutral gauge boson of SU(2), and in any case it doesn’t describe electromagnetism without postulating unphysically that positrons are electrons ‘going backwards in time’; however this kind of objection is an issue you will get with new theories due to problems in the bedrock assumptions of the subject and so such issues should not be used as an excuse to censor the new idea out; in this case the problem is resolved either by Feynman’s speculative time argument – speculative because there is no evidence that positive charges are negative charges going back in time! – or as suggested on this blog, by dumping U(1) symmetry for electrodynamics and adopting instead SU(2) for electrodynamics without the Higgs field, which then allows two charges – positive and negative without one going backwards in time, and three massless gauge bosons and can therefore incorporate gravitation with electrodynamics. Evidence from electromagnetism:
‘I am a physicist and throughout my career have been involved with issues in the reliability of digital hardware and software. In the late 1970s I was working with CAM Consultants on the reliability of fast computer hardware. At that time we realised that interference problems – generally known as electromagnetic compatibility (emc) – were very poorly understood.’
– Dr David S. Walton, co-discoverer in 1976 (with Catt and Malcolm Davidson) that the charging and discharging of capacitors can be treated as the charging and discharging of open ended power transmission lines. This is a discovery with a major but neglected implication for the interpretation of Maxwell’s classical electromagnetism equations in quantum field theory; because energy flows into a capacitor or transmission line at light velocity and is then trapped in it with no way to slow down – the magnetic fields cancel out when energy is trapped – charged fields propagating at the velocity of light constitute the observable nature of apparently ‘static’ charge and therefore electromagnetic gauge bosons of electric force fields are not neutral but carry net positive and negative electric charges. Electronics World, July 1995, page 594.
Above: the Catt-Davidson-Walton theory showed that the transmission line section as capacitor could be modelled by the Heaviside theory of a light-velocity logic pulse. The capacitor charges up in a lot of small steps as voltage flows in, bounces off the open circuit at the far end of the capacitor, and then reflects and adds to further incoming energy current. The steps are approximated by the classical theory of Maxwell, which gives the exponential curve. Unfortunately, Heaviside’s mathematical theory is an over-simplification (wrong physically, although for most purposes it gives approximately valid results numerically) because it assumes that at the front of a logic step (Heaviside signalled using Morse code in 1875 in the undersea cable between Newcastle and Denmark) the rise is a discontinuous or abrupt step, instead of a gradual rise! We know this is wrong because at the front of a logic step the gradual rise in electric field strength with distance is what causes conduction electrons to accelerate to drift velocity from the normal randomly directed thermal motion they have.
Above: some of the errors in Heaviside’s theory are inherited by Catt in his theoetical work and in his so-called “Catt Anomaly” or “Catt Question”. If you look logically at Catt’s original anomaly diagram (based on Heaviside’s theory), you can see that no electric current can occur: electric current is caused by the drift of electrons which is due to the change of voltage with distance along a conductor. E.g. if I have a conductor uniformly charged to 5 volts with respect to another conductor, no electric current flows because there is simply no voltage gradient to cause a current. If you want an electric current, connect one end of a conductor to say 5 volts and the other end to some different potential, say 0 volts. Then there is a gradient of 5 volts along the length of the conductor, which accelerates electrons up to drift velocity for the resistance. if you connect both ends of a conductor to the same 5 volts potential, there is no gradient in the voltage along the conductor so there is no net electromotive force on the electrons. The vertical front on Catt’s original Heaviside diagram depiction of the “Catt Anomaly” doesn’t accelerate electrons in the way that we need because it shows an instantaneous rise in volts, not a gradient with distance.
Once you correct some of the Heaviside-Catt errors by including a real (ramping) rise time at the front of the electric current, the physics at once becomes clear and you can see what is actually occurring. The acceleration of electrons in the ramps of each conductors generates a radiated electromagnetic (radio) signal which propagates transversely to the other conductor. Since each conductor radiates an exactly inverted image of the radio signal from the other conductor, both superimposed radio signals exactly cancel when measured from a large distance compared to the distance between the two conductors. This is perfect interference, and prevents any escape of radiowave energy in this mechanism. The radiowave energy is simply exchanged between the ramps of the logic signals in each of the two conductors of the transmission line. This is the mechanism for electric current flow at light velocity via power transmission lines: what Maxwell attributed to ‘displacement current’ of virtual charges in a mechanical vacuum is actually just exchange of radiation!
There are therefore three related radiations flowing in electricity: surrounding one conductor there are positively-charged massless electromagnetic gauge bosons flowing parallel to the conductor at light velocity (to produce the positive electric field around that conductor), around the other there are negatively-charged massless gauge bosons going in the same direction again parallel to the conductor, and between the two conductors the accelerating electrons exchange normal radiowaves which flow in a direction perpendicular to the conductors and have the role which is mathematically represented by Maxwell’s ‘displacement current’ term (enabling continuity of electric current in open circuits, i.e. circuits containing capacitors with a vacuum dielectric that prevents stops real electric current flowing, or long open-ended transmission lines which allow electric current to flow while charging up, despite not being a completed circuit).
Commenting on the mainstream focus upon string theory, Dr Woit states (http://arxiv.org/abs/hep-th/0206135 page 52):
‘It is a striking fact that there is absolutely no evidence whatsoever for this complex and unattractive conjectural theory. There is not even a serious proposal for what the dynamics of the fundamental “M-theory” is supposed to be or any reason at all to believe that its dynamics would produce a vacuum state with the desired properties. The sole argument generally given to justify this picture of the world is that perturbative string theories have a massless spin two mode and thus could provide an explanation of gravity, if one ever managed to find an underlying theory for which perturbative string theory is the perturbation expansion. This whole situation is reminiscent of what happened in particle theory during the 1960’s, when quantum field theory was largely abandoned in favor of what was a precursor of string theory. The discovery of asymptotic freedom in 1973 brought an end to that version of the string enterprise and it seems likely that history will repeat itself when sooner or later some way will be found to understand the gravitational degrees of freedom within quantum field theory. While the difficulties one runs into in trying to quantize gravity in the standard way are well-known, there is certainly nothing like a no-go theorem indicating that it is impossible to find a quantum field theory that has a sensible short distance limit and whose effective action for the metric degrees of freedom is dominated by the Einstein action in the low energy limit. Since the advent of string theory, there has been relatively little work on this problem, partly because it is unclear what the use would be of a consistent quantum field theory of gravity that treats the gravitational degrees of freedom in a completely independent way from the standard model degrees of freedom. One motivation for the ideas discussed here is that they may show how to think of the standard model gauge symmetries and the geometry of space-time within one geometrical framework.’
That last sentence is the key idea that gravity should be part of the gauge symmetries of the universe, not left out as it is in the mainstream ‘standard model’, U(1) x SU(2) x SU(3).
How the pressure mechanism of quantum gravity reproduces the contraction in general relativity
As long ago as 1949 a Dirac sea was shown to mimic the relativity contraction and mass-energy:
‘It is shown that when a Burgers screw dislocation [in a crystal] moves with velocity v it suffers a longitudinal contraction by the factor (1 – v2/c2)1/2, where c is the velocity of transverse sound. The total energy of the moving dislocation is given by the formula E = Eo/(1 – v2/c2)1/2, where E0 is the potential energy of the dislocation at rest.’ – C. F. Frank, ‘On the equations of motion of crystal dislocations’, Proceedings of the Physical Society of London, vol. A62 (1949), pp. 131-4.
Feynman explained that the contraction of space around a static mass M due to curvature in general relativity is a reduction in radius by (1/3)MG/c2 which is 1.5 mm for the Earth. You don’t need the tensor machinery of general relativity to get such simple results for the low energy (classical) limit. (Baez and Bunn similarly have a derivation of Newton’s law from general relativity, that doesn’t use tensor analysis: see http://math.ucr.edu/home/baez/einstein/node6a.html.) We can do it just using the equivalence principle of general relativity plus some physical insight:
The velocity needed to escape from the gravitational field of a mass M (ignoring atmospheric drag), beginning at distance x from the centre of the mass is by Newton’s law v = (2GM/x)1/2, so v2 = 2GM/x. The situation is symmetrical; ignoring atmospheric drag, the speed that a ball falls back and hits you is equal to the speed with which you threw it upwards. This is just a simple result of the conservation of energy! Therefore, the gravitational potential energy of mass in a gravitational field at radius x from the centre of mass is equivalent to the energy of an object falling down to that distance from an infinite distance, and this gravitational potential energy is – by the conservation of energy – equal to the kinetic energy of a mass travelling with escape velocity v.
By Einstein’s principle of equivalence between inertial and gravitational mass, the effects of the gravitational acceleration field are identical to other accelerations such as produced by rockets and elevators. Therefore, we can place the square of escape velocity (v2 = 2GM/x) into the Fitzgerald-Lorentz contraction, giving g = (1 – v2/c2)1/2 = [1 – 2GM/(xc2)]1/2
However, there is an important difference between this gravitational transformation and the usual Fitzgerald-Lorentz transformation, since length is only contracted in one dimension with velocity, whereas length is contracted equally in 3 dimensions (in other words, radially outward in 3 dimensions, not sideways between radial lines!), with spherically symmetric gravity. Using the binomial expansion to the first two terms of each:
Fitzgerald-Lorentz contraction effect: g = x/x0 = t/t0 = m0/m = (1 – v2/c2)1/2 = 1 – ½v2/c2 + …
Gravitational contraction effect: g = x/x0 = t/t0 = m0/m = [1 – 2GM/(xc2)]1/2 = 1 – GM/(xc2) + …,
where for radial symmetry (x = y = z = r), we have the contraction spread over three perpendicular dimensions not just one as is the case for the FitzGerald-Lorentz contraction: x/x0 + y/y0 + z/z0 = 3r/r0. Hence the relative radial contraction of space around a mass is r/r0 = 1 – GM/(xc2) = 1 – GM/[(3rc2]
Therefore, clocks slow down not only when moving at high velocity, but also in gravitational fields, and distance contracts in all directions toward the centre of a static mass. The variation in mass with location within a gravitational field shown in the equation above is due to variations in gravitational potential energy. Space is contracted radially around mass M by the distance (1/3)GM/c2.
It is not contracted in the transverse direction, i.e. along the circumference of the Earth (the direction at right angles to the radial lines which originate from the centre of mass). This is the physical explanation in quantum gravity of so-called curved spacetime: because graviton exchange compresses masses radially but leaves them unaffected transversely, radius is reduced but circumference is unaffected so the value of Pi (circumference/diameter of a circle) would be altered for a massive circular object if we use Euclidean 3-dimensional geometry! General relativity’s spacetime is a system for keeping Pi from changing by simply invoking an extra dimension: by treating time as a spatial dimension, Euclidean 3-dimensional space can be treated as a surface on 4-dimensional spacetime, with the curvature ensuring that Pi is never altered! Spacetime curves due to the extra dimension instead of Pi altering. However, this is a speculative explanation and there is no proof that contraction effects are really due to this curvature. For example, Lunsford published a unification of electrodynamics and general relativity which 6 dimensions including 3 time-like dimensions, so that there is a perfect symmetry between space and time, with each spatial dimension having a corresponding time dimension. This makes sense when you measure time from the big bang by means of the t = 1/H where H is the Hubble parameter H = v/x: because there are 3 spatial dimensions, the expansion rate measured in each of those three spatial dimensions will give you 3 separate ages of the universe, i.e. 3 time dimensions (unless the expansion is isotropic, when all three times are indistinguishable, as appears to be the case!). (As with a paper of mine, Lunsford’s paper was censored off arXiv after being published in a peer-reviewed physics journal under the title, “Gravitation and Electrodynamics over SO(3,3)”, International Journal of Theoretical Physics, Volume 43, Number 1 / January, 2004, Pages 161-177, because it disagrees with the number of speculative unobserved dimensions in arXiv endorsed mainstream string theory sh*t: it can be downloaded here. Therefore when ‘string theorists’ claim that there is ‘no alternative’ to their brilliant sh*t landscape of 10500 metastable vacua solutions from all the combinations of 6 unobservable, compactified Calabi-Yau extra spatial dimensions in 10 dimensional string, tell them and their stupid arXiv censors to go and f*ck off with their extra spatial dimensions insanity.)
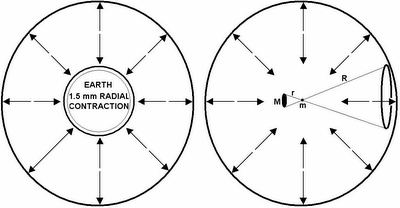
Above: Feynman’s illustration of general relativity by the 1.5 mm radial contraction of the Earth. Experiments like the Casimir effect demonstrate that the vacuum is filled with virtual bosonic quantum radiation which causes forces. When you move in this sea of bosonic radiation, you experience inertia (resistance to acceleration) from the radiation, and during your acceleration you get contracted in the direction of motion. Gravitational fields have a similar effect; graviton exchange radiation pressure contracts masses radially but not transversely, so the radius of the Earth is contracted by 1.5 mm, but the circumference isn’t affected. Hence there would be a slight change to Pi if space is Euclidean. This is why in general relativity 3-dimensional space is treated as a curved surface on a 4-dimensional spacetime, so that curvature of 3-dimensional space keeps Pi from being altered. However, in quantum gravity we have a physical mechanism for the contraction so the 4-dimensional spacetime theory and ‘curved space’ is just a classical approximation or calculating trick for the real quantum gravity effects! Gravitational time-dilation accompanies curvature because all measures of time are based on motion, and the contraction of distance means that moving clock parts (including things like oscillating electrons, oscillating quartz crystal atoms, etc) travel a smaller distance in a given time, making time appear to slow down. It also applies to the electric currents in nerve impulses, so a the electric impulses in person’s brain will move a smaller distance in a given interval of time, making the person slow down: everything slows down in time-dilation. Professor Richard P. Feynman explains this time-dilation effect on page 15-6 of volume 1 of The Feynman Lectures on Physics (Addison Wesley, 1963) by considering the motion of light inside a clock:
‘… it takes a longer time for light to go from end to end in the moving clock than in the stationary clock. Therefore the apparent time between clicks is longer for the moving clock … Not only does this particular kind of [light-based] clock run more slowly, but … any other clock, operating on any principle whatsoever, would also appear to run slower, and in the same proportion …
‘Now if all moving clocks run slower, if no way of measuring time gives anything but a slower rate, we shall just have to say, in a certain sense, that time itself appears to be slower in a space ship. All the phenomena there – the man’s pulse rate, his thought processes, the time he takes to light a cigar, how long it takes to grow up and get old – all these things must be slowed down in the same proportion, because he cannot tell he is moving.’
Reference frame for the calculations
The confirmation that the universe has a small positive (outward) acceleration via computer-automated CCD-telescope observations of the signature flashes of distant, redshifted supernovae in 1998 confirmed the prediction of a = Hc made in 1996 and published via Electronics World (October 1996, letters pages) and Science World (ISSN 1367-6172), February 1997. But regardless of the fact that we predicted it before it was observed, the acceleration is well confirmed by observations and is therefore a fact. It is an acceleration seen from our frame of reference on the universe, in which we are looking back in time by the amount x/c when we look out to distance x, due to the delay time in light reaching us. Gravitational fields propagate at the velocity of light according to the empirically defensible basics of general relativity (which has little to do with its fitting to cosmology with arbitrary ad hoc adjustment factors). So the reference frame for calculating the force of the outward accelerating matter of the universe is that of the observer, for whom the surrounding universe has a small apparent acceleration and large apparent mass, giving a large outward force, F = ma.
Suppose we look to distance R. We’re looking to earlier times due to the travel time of light to us! The age of the universe t at distance R plus the time light takes to travel from distance R to us T is equal to 1/H in flat spacetime: t + T = 1/H.
Suppose a supernova is a billion light years away. In that case
t = 13.7 – 1 = 12.7 billion years after big bang
T = 1 billion years light travel time to reach us
T + t = 13.7 billion years = 1/H, in the observed (flat) spacetime. This is a simple fact!
Hence Hubble’s empirical law tells us another simple fact, namely that the distant supernova is subject to acceleration as seen from our frame of reference:
v = HR = H(cT) = Hc[(1/H) – t] = c – (Hct)
a = dv/dt = d[c – (Hct)]/dt = –Hc = -6×10-10 ms-2
This is a tiny cosmological acceleration, only observable when looking very distant objects, so you have to observe constant energy (Type IA) supernova explosions in order to have a bright enough flash of light to observe redshifted spectra from that distance. This is what was discovered in 1998 by two teams of astronomers, led respectively by Saul Perlmutter of the Lawrence Berkeley National Laboratory and by Brian Schmidt of the Australian National laboratory.
Above: in 1998 two independent groups, the High-z Supernova Search Team (Riess et al., Astronomical Journal, pages 116 and 1009, 1998) and the Supernova Cosmology Project (Perlmutter et al., Astrophysical Journal, 1999, pages 517 and 565) both came up with observational evidence that the universe is accelerating, not slowing down due to gravitation as had been expected from Friedmann’s metric of general relativity. So cosmologists quickly introduced an ad hoc ‘correction’ in the form of a cosmological constant (lambda) to make the universe 70% dark energy and 30% matter (most of this being dark matter which has never been directly observed in the laboratory; only 5% of it is normal matter and another 5% seems to be neutrinos and antineutrinos). For a criticism of the resulting ad hoc lambda-CDM ‘theory’ see the paper by Richard Lieu of the Physics Department, University of Alabama, ‘Lambda-CDM cosmology: how much suppression of credible evidence, and does the model really lead its competitors, using all evidence?’, http://arxiv.org/abs/0705.2462.
However, the acceleration itself which offsets gravitational attraction at great distances is not in question. The Type IA supernovae all release a similar amount of energy (7*1026 megatons of TNT equivalent; 3*1042 J) because they result from the collapse of white dwarfs when their mass just exceeds 1.4 times the mass of the sun (the Chandrasekhar limit). When this mass limit is exceeded (due to matter from a companion star falling into the white dwarf), the free electron gas in the white dwarf can no longer support the star against gravity, so the white dwarf collapses due to gravity, releasing a lot of gravitational potential energy which heats the star up to such a high temperature and pressure that the nuclei of carbon and oxygen can then fuse together, creating large amounts of radioactive nickel-56, and a massive explosion in space called a supernova. These Type IA supernovae occur roughly once every 400 years in the Milky Way galaxy. They all have a similar light spectrum regardless of distance from us, indicating that they are similar in composition. So their relative brightness indicates their distance from us (by the inverse-square law of radiation) while the redshift of the line spectra, such as lines from nickel-56, indicates recession velocity. Redshift is only explained by recession.
Now consider how this prediction of the cosmological aceleration differs from the mainstream treatment of cosmological acceleration and dark energy. Professor Sean Carroll, who uses Feynman’s old desk, has a paper here called ‘Why is the Universe Accelerating?’ Einstein’s field equation of general relativity relates the geometry of spacetime (i.e., the curvature of space which would be needed to cause accelerations if space is non-quantum but is instead a continuum that can be curved by the presence of a fourth, time-like dimension) to the sources of gravitational fields (i.e., the supposed continuum curvature) such as mass-energy, pressure etc.
Because of relativistic effects on the source of the gravitational field (i.e., accelerating bodies contract in the direction of motion and gain mass, which is gravitational charge, so a falling apple becomes heavier while it accelerates), the curvature of spacetime is affected in order for energy to be conserved when the gravitational source is changed by relativistic motion. This means that the Ricci tensor for curvature is not simply equal to the source of the gravitational field. Instead, another factor (equal to half the product of the trace of the Ricci tensor and the metric tensor) must be subtracted from the Ricci curvature to ensure the conservation of energy. As a result, general relativity makes predictions which differ from Newtonian physics. General relativity is correct as far as it goes, which is mathematical generalization of Newtonian gravity and a correction for energy conservation. It’s not, however, the end of the story. There is every reason to expect general relativity to hold good in the solar system, and to be a good approximation. But if gravity has a gauge theory (exchange radiation) mechanism in the expanding universe which surrounds a falling apple, there is a reason why general relativity is incomplete when applied to cosmology.
Sean’s paper ‘Why is the Universe Accelerating?’ asks why the energy of the vacuum is so much smaller than predicted by grand unification theories of supersymmetry, such as supergravity (a string theory). This theory states that the universe is filled with a quantum field of virtual fermions which have a ground state or zero-point energy of E = (1/2){h-bar}{angular frequency}. Each of these oscillating virtual charges radiates energy E = hf, so integrating over all frequencies gives you the total amount of vacuum energy. This is infinity if you integrate frequencies between zero and infinity, but this problem isn’t real because the highest frequencies are the shortest wavelengths, and we already know from the physical need to renormalize quantum field theory that the vacuum has a minimum size scale (the grain size of the vacuum), and you can’t have shorter wavelengths (or corresponding higher frequencies) than that size. Renormalization introduces cutoffs on the running couplings for interaction strengths; such couplings would become infinite at zero distance, causing infinite field momenta, if they were not cutoff by a vacuum grain size limit. The mainstream string and other supersymmetric unification ideas assume that the grain size is the Planck length although there is no theory of this (dimensional analysis isn’t a physical theory) and certainly no experimental evidence for this particular grain size assumption, and a physically more meaningful and also smaller grain size would be the black hole horizon radius for an electron, 2GM/c2.
But to explain the mainstream error, the assumption of the Planck length as the grain size tells the mainstream how closely grains (virtual fermions) are packed together in the spacetime fabric, allowing the vacuum energy to be calculated. Integrating the energy over frequencies corresponding to vacuum oscillator wavelengths which are longer than the Planck scale gives us exactly the same answer for the vacuum energy as working out the energy density of the vacuum from the grain size spacing of virtual charges. This is the Planck mass (expressed as energy using E = mc2) divided into the cube of the Planck length (the volume which each of the supposed virtual Planck mass vacuum particles is supposed to occupy within the vacuum).
The answer is 10112 ergs/cm3 in Sean’s quaint American stone age units, or 10111 Jm-3 in physically sensible S.I. units (1 erg is 10-7 J, and there are 106 cm3 in 1 m3). The problem for Sean and other mainstream people is why the measured ‘dark energy’ from the observed cosmological acceleration implies a vacuum energy density of merely 10-9 Jm3. In other words, string theory and supersymmetric unification theories in general exaggerate the vacuum energy density by a factor of 10111 Jm-3/10-9 Jm-3 = 10120.
That’s an error! (although, of course, to be a little cynical, such errors are common in string theory, which also predicts 10500 different universes, exceeding the observed number).
Now we get to the fun part. Sean points out in section 1.2.2 ‘Quantum zero-point energy’ at page 4 of his paper that:
‘This is the famous 120-orders-of-magnitude discrepancy that makes the cosmological constant problem such a glaring embarrassment. Of course, it is somewhat unfair to emphasize the factor of 10120, which depends on the fact that energy density has units of [energy]4.’
What Sean is saying here is that the mainstream-predicted vacuum energy density is at since the Planck length is inversely proportional to the Planck energy, the vacuum energy density of {Planck energy}/{Planck length3} ~ {Planck energy4} which exaggerates the error in the prediction of the energy. So if we look at the error in terms of energy rather than energy density for the vacuum, the error is only a factor of 1030, not 10120.
What is pretty obvious here is that the more meaningful 1030 error factor is relatively close to the factor 1040 which is the ratio between the coupling constants of electromagnetism and gravity. In other words, the mainstream analysis is wrong in using the electromagnetic (electric charge) oscillator photon radiation theory, instead of the mass oscillator graviton radiation theory: the acceleration of the universe is due to graviton exchange.
In a blog post dated 2004, Sean wrote:
‘Yesterday we wondered out loud whether cosmological evidence for dark matter might actually be pointing to something more profound: a deviation of the behavior of gravity from that predicted by Einstein’s general relativity (GR). Now let’s ask the same question in the context of dark energy and the acceleration of the universe. … For example, maybe general relativity works for ordinary bound systems like stars and galaxies, but breaks down for cosmology, in particular for the expansion rate of the universe. In GR the expansion rate is described by the Friedmann equation … So maybe Friedmann was somehow wrong. For example, maybe we can solve the problem of the mismatch between theory and experiment by saying that the vacuum energy somehow doesn’t make the universe accelerate like ordinary energy does.’
Duh! The error is the assumption of fundamental force unification, which would make all the fundamental interaction couplings identical at the unification energy:
Above: supersymmetry which is based on the false guess that, at very high energy, all fundamental force couplings have the same numerical value; to be specific, the minimal supersymmetric standard model – the one which contains 125 parameters instead of just the 19 in the standard model – makes all force couplings coincide at alpha = 0.04, near the Planck scale. Although this extreme prediction can’t be tested, quite a lot is known about the strong force at lower and intermediate energies from nuclear physics and also from various particle experiments and observations of very high energy cosmic ray interactions with matter, so, in the book Not Even Wrong (UK edition), Dr Woit explains on page 177 that – using the measured weak and electromagnetic forces – supersymmetry predicts the strong force incorrectly high by 10-15%, when the experimental data is accurate to a standard deviation of about 3%. At the top of the diagram above is the theory that there is no ‘unification’ of force couplings at high energy, and that the unification instead consists of energy conservation for the different fields at high energy.
The relative strength of electromagnetic interactions has been experimentally observed (in electron scattering) to increase from Coulomb’s low-energy law by 7% as the collision energy increases from about 0.5 MeV to about 90 GeV (I. Levine, D. Koltick, et al., Physical Review Letters, v.78, 1997, no.3, p.424), but the strong force behaves differently, falling as energy increases (except for a peaking effect at relatively low energy), as if the strong force is powered by gauge bosons created in the vacuum from the energy that the virtual fermions in the vacuum absorb from the electromagnetic field in the act of being radially polarized by that electromagnetic field, the virtual fermions being unleashed from the ground state of the vacuum by pair production in electric fields exceeding Schwinger’s 1018 volts/metre IR cutoff (equation 359 in Dyson’s http://arxiv.org/abs/quant-ph/0608140 and equation 8.20 in Luis Alvarez-Gaume, and Miguel A. Vazquez-Mozo’s http://arxiv.org/abs/hep-th/0510040):
‘All charges are surrounded by clouds of virtual photons, which spend part of their existence dissociated into fermion-antifermion pairs. The virtual fermions with charges opposite to the bare charge will be, on average, closer to the bare charge than those virtual particles of like sign. Thus, at large distances, we observe a reduced bare charge due to this screening effect.’ – I. Levine, D. Koltick, et al., Physical Review Letters, v.78, 1997, no.3, p.424.
‘The cloud of virtual particles acts like a screen or curtain that shields the true value of the central core. As we probe into the cloud, getting closer and closer to the core charge, we ’see’ less of the shielding effect and more of the core. This means that the electromagnetic force from the electron as a whole is not constant, but rather gets stronger as we go through the cloud and get closer to the core. Ordinarily when we look at or study an electron, it is from far away and we don’t realize the core is being shielded.’ – Professor David Koltick
‘… we [experimentally] find that the electromagnetic coupling grows with energy. This can be explained heuristically by remembering that the effect of the polarization of the vacuum … amounts to the creation of a plethora of electron-positron pairs around the location of the charge. These virtual pairs behave as dipoles that, as in a dielectric medium, tend to screen this charge, decreasing its value at long distances (i.e. lower energies).’ – arxiv hep-th/0510040, p 71.
What these people don’t consider is what happens to the electromagnetic field energy which is absorbed by the virtual fermions within 1 femtometre from a particle core! It turns out that this energy powers short-range interactions. The way unification works isn’t by making force strengths equal at a very high energy, it’s by sharing energy via the absorption of electromagnetic field energy by polarized virtual fermions close to core of a real particle. The energy density of an electromagnetic field is known as a function of field strength, and the field strength can be calculated for any distance from an electric charge using Maxwell’s equations (specifically Gauss’s law, the electric field form of Coulomb’s force law). There is no positive evidence for coupling strength unification, there is some evidence (quoted by Woit, as explained) that it is in error, and is a good reason – from energy conservation – why the fact that the strong interaction charge gets bigger with increasing distance (out to a certain limit!) requires the fact that it is powered from energy being absorbed over that distance from the electromagnetic field by virtual fermions!
Furthermore, since quantum gravity is a two-step mechanism with gravitons only interacting with observed particles via an intermediary unobserved Higgs-type field that provides ‘gravitational charge’ to mass-energy, then we must face the possibility that gravitons don’t necessarily have gravitational charge (mass). In this case, gravitational couplings don’t run, but stay small at all distances and energies. This is the reason why the unification theory overestimates the cosmological acceleration of the universe:
The acceleration is caused by gravitons, and since gravitons don’t carry gravitational charge (only the Higgs-like field is charged) they are like the photons in the old gauge theory of U(1) electrodynamics and don’t interact with one another to cause the coupling to increase at short distances or high collision energies. Since the gravity coupling actually remains small at high energies and small distances, and since it is powering the cosmological acceleration, we can see why the mainstream assumption that gravity is enhanced by a factor of 1040 at the smallest distances causes the mainstream estimate of cosmological acceleration/dark energy to be too high (another error, albeit a smaller one, in the mainstream calculation is their assumption of the Planck scale as the grain size or cutoff wavelength instead of the black hole event horizon size, which is smaller and more meaningful physically than the bigger length given by Planck’s arbitrary dimensional analysis).
(On related topic, it is a fact that gravity waves haven’t been observed from the acceleration and oscillation of gravitational charges (masses) unlike the observation of electromagnetic waves from accelerating and oscillating electric charges, precisely because the gravity coupling is 1040 times smaller than the electromagnetic coupling. Gravity waves are related to gravitons in the way that photons of light are related to virtual photons that mediate electromagnetic fields.)
Pair-production, vacuum polarization, and the physical explanation of the IR and UV cutoffs which prevent infinities in quantum field theory
The so-called ultraviolet (UV) divergence problem in quantum field field is having to take an upper limit cutoff for the charge renormalization to prevent a divergence of loops of massive nature occurring at extremely high energy. The solution to this problem is straightforward (it is not a physically real problem): there physically just isn’t room for massive loops to be polarized above the UV cutoff because at higher energy you get closer to the particle core, so the space is simply too small in size to have massive loops with charges being polarized along the electric field vector. There is a normally unobservable Dirac sea in the vacuum which affects reality when charges in it gain enough energy close to allow pairs of fermions to pop into observable existence close to electrons where the electric field strength is above Schwinger’s pair-production cut-off, 1.3*1018 volts/metre. This lower limit on the energy required for pair-production explains physically the cause for the IR cutoff on running couplings and loop effects in quantum field theory. The UV cutoff at extremely high energy is also explained by a correspondingly simple mechanism: at high energy, the corresponding distance is so small there is not likely to be any Dirac sea particles available in that small space (i.e., the distance becomes smaller than the ultimate grain-size of the vacuum, or the physical size of normally unobservable ground state Dirac sea fermions), so you physically can’t get pair production or vacuum polarization because the distance is too small to allow those processes to occur! So the intense electric field strength is unable to produce any massive loops if the distance is smaller than the distance you are applying your calculations to is smaller than the size of the vacuum particles:
‘It always bothers me that, according to the laws as we understand them today, it takes a computing machine an infinite number of logical operations to figure out what goes on in no matter how tiny a region of space, and no matter how tiny a region of time. How can all that be going on in that tiny space? Why should it take an infinite amount of logic to figure out what one tiny piece of space/time is going to do? So I have often made the hypothesis that ultimately physics will not require a mathematical statement, that in the end the machinery will be revealed, and the laws will turn out to be simple, like the chequer board with all its apparent complexities.’
– R. P. Feynman, Character of Physical Law, November 1964 Cornell Lectures, broadcast and published in 1965 by BBC, pp. 57-8.
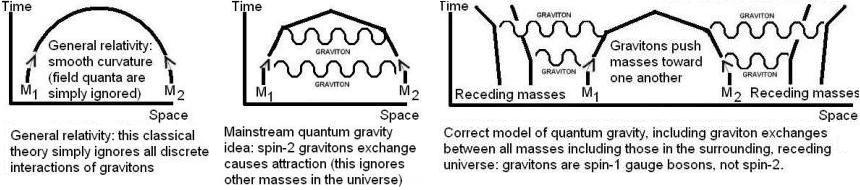
Above: how graviton exchanges cause both the attaction of masses which are nearby (compared to the size scale of the universe) and small (compared to the mass of the universe) and the repulsion of masses which are at relatively large distances (using the size scale of the universe) and large (using the mass of the universe). Think of a raisin cake baking: the dough exerts pressure and pushes nearby raisins together (because there is not much dough pressure between them, but lots of dough pressure acting on the other sides!) while pushing distant raisins apart. There is no genius required to see that the long-distance repulsion of mass inherent in the acceleration of the universe is caused by gravitons which cause ‘attraction’ locally.
Consider the force stength (coupling constant) in addition to the inverse-square law: Heisenberg’s uncertainty principle says that the product of the uncertainties in momentum and distance is at least h-bar. Let uncertainty in momentum p = mc, and the uncertainty in distance be x = ct. Hence the product of momentum and distance, px = (mc).(ct) = (mc2t = Et = h-bar, where E is energy (Einstein’s mass-energy equivalence). This Heisenberg relationship (the product of energy and time equalling h-bar) is used in quantum field theory to determine the relationship between particle energy and lifetime: E = h-bar/t. The maximum possible range of a virtual particle is equal to its lifetime t multiplied by c. Now for the slightly clever bit:
px = h-bar implies (when remembering p = mc, and E = mc2):
x = h-bar /p = h-bar /(mc) = h-bar*c/E
so E = h-bar*c/x
when using the classical definition of energy as force times distance (E = Fx):
F = E/x = (h-bar*c/x)/x
= h-bar*c/x2
So we get the force strength, and we just need to remember that this inverse-square law only holds for ranges shorter than the limiting distance a particle can go at nearly c (if relativistic) in the time allowed by the uncertainty principle, x = h-bar /p = h-bar /(mc) = h-bar*c/E. Notice that the force strength this treatment gives for repulsion between two electrons is 137.036… times the force given by Coulomb’s law. This can be explained by the vacuum polarization or virtual fermions around a charge core screening the core electric charge by the 137.036 factor, so that a proportionately lower electric charge and Coulomb force is observed at a distance beyond a few femtometres from an electron core. (This effect was experimentally confirmed by Koltick et al., in high energy electron scattering experiments published in the journal Physical Review Letters in 1997.)
What is important to notice is that this treatment from quantum theory naturally gives the electromagnetic force result, not gravity, which is about 1040 times weaker. So the cosmological acceleration estimated from the mainstream treatment of photon radiation from oscillating virtual electric charges in the ground state of the vacuum will exaggerate the graviton emission from oscillating virtual gravitational charges (masses) in the ground state of the vacuum by a similar factor.
The graviton exchanges between masses will cause expansion on cosmological distance scales and attraction of masses over smaller distances! If masses are significantly redshifted, the exchanged gravitons between them push them apart (cosmological acceleration, dark energy); if they aren’t receding they won’t exchange gravitons with a net force, so the gravitons which are involved then are those exchanged between each mass and the distant receding masses in the universe. Because nearby masses don’t exchange gravitons forcefully, they shield one another from gravitons coming from distant masses in the direction of the other (nearby) mass, and so get pushed together.
That ‘attraction’ and repulsion can both be caused by the same spin-1 gravitons (which are dark energy) can be understood by a semi-valid analogy, the baking raisin cake. As the cake expands, the distant raisins in it recede with the expansion of the cake, as if there is a repulsion between them. But nearby raisins in the cake will be pressed even closer together by the surrounding pressure from the dough on each side (the dough – not the raisins – is what physically expands as carbon dioxide is released in it from yeast or baking soda), because the raisins are being pressed on all sides apart from the sides facing nearby adjacent raisins. So because there is no significant pressure of dough inbetween them but plenty of dough pressure from other directions, nearby raisins shield one another and so get pressed closer together by the expansion of the surrounding dough! Therefore, the raisin cake analogy serves to show how one physical process – a pressure in space against mass-energy created by graviton exchange radiation – causes both the repulsion that accelerates the expansion of the universe on large scales, as well as causing the attraction of gravity on smaller distance scales where the masses involved are not substantially receding (redshifted) from one another.
Above: think of the analogy of a raisin cake expanding due to the motion of the baking dough. Nearby raisins (with little or no dough between them) will be pushed closer together like ‘attraction’ because there is little or no dough pressure between them but a lot of dough pressure from other directions, while distant raisins will be accelerated further apart during the cooking because they will have a lot of expanding dough around them on all sides, causing a ‘repulsion’ effect. So there are two phenomena – cosmological repulsive acceleration and gravitation – provided for the price of one graviton field! No additional dark energy or CC, just the plain old gravitational field. I think this is missed by the mainstream because:
(1) they think LeSage came up with quantum gravity and was disproved (he didn’t, and the objections to his ideas came because he didn’t have gravitons exchange radiation, but a gas), and
(2) they believe the false Pauli-Fierz ‘proof’ that gravitons exchanged between 2 masses to cause them to attract, must suck, which implies spin-2 suckers.
Actually the Pauli-Fierz proof is fine if the universe only contains 2 masses which ‘attract’. Problem is, the universe doesn’t just contain 2 masses. Instead, we’re surrounded by masses, clusters of immense receding galaxies with enormous redshift and accelerating with a large outward force away from us in all directions, and there is no mechanism to stop graviton exchanges with those masses and the two little masses in our study. As the gravitons propagate from such distant masses to the two little nearby ones we are interested in, they converge (not diverge), so the effects of the distant masses are larger (not smaller) that that of nearby masses. This destroys the mainstream ‘proof’ using path integrals that aims to show that spin-2 gravitons are required to provide universal attraction, because the path integral is no longer that between just two lumps of mass-energy. It must take account of all the mass-energy in the whole universe, as in Fig. 1 above. Richard P. Feynman points out in The Feynman Lectures on Gravitation, page 30, that gravitons do not have to be spin-2, which has never been observed!
As explained in the earlier blog post on path integrals, for the low energy situations that constitute long-range force field effects, you don’t have pair production loops, so there is only one kind of simple (‘tree’ type) Feynman diagram (without loops and with just a single interaction vertex) involved in the path integral, and the integral is just summing that one kind of interaction over all geometric possibilities to reproduce classical physics: this is exactly what we do in Fig. 1 above. (Feynman shows in his book QED that for low energy physics, the path integral formulation reduces to the classical limit of simply finding the path of least action for a light ray where most paths have different phases which cancel out; the case of spin-1 quantum gravity by analogy reduces to the situation whereby most graviton exchanges produce force effects that geometrically cancel out, so the resultant is due to asymmetry and is simple to calculate.)
Once you include the masses of the surrounding universe in the path integral, the whole basis of the Pauli-Fietz proof evaporates; gravitons no longer need to be suckers and thus don’t need to have a spin of 2. Instead of having spin-2 gravitons sucking 2 masses together in an otherwise empty universe, you really have those masses being pushed together by graviton exchanges with the immense masses in the surrounding universe. This is so totally obvious, it’s amazing why the mainstream is so obsessed with spin-2 suckers. (Probably because string theory is the framework for spin-2 suckers.)
‘The problem is not that there are no other games in town, but rather that there are no bright young players who take the risk of jeopardizing their career by learning and expanding the sophisticated rules for playing other games.’
– Prof. Bert Schroer, http://arxiv.org/abs/physics/0603112, p46
‘It is said that more than 200 theories of gravitation have have been put forward; but the most plausible of these have all had the defect that that they lead nowhere and admit of no experimental test.’
– A. S. Eddington, Space Time and Gravitation, Cambridge University Press, 1920, p64. This problem continues with Witten’s stringy hype:
‘String theory has the remarkable property of predicting gravity.’ [He means spin-2 gravitons, which don’t lead to any facts about gravity.]
– Edward Witten, superstring 10/11 dimensional M-theory originator, ‘Reflections on the Fate of Spacetime’, Physics Today, April 1996.
Spin of gauge boson
‘In the particular case of spin 2, rest-mass zero, the equations agree in the force-free case with Einstein’s equations for gravitational waves in general relativity in first approximation …’ – Conclusion of the paper by M. Fierz and W. Pauli, ‘On relativistic wave equations for particles of arbitrary spin in an electromagnetic field’, Proc. Roy. Soc. London., volume A173, pp. 211-232 (1939). [Notice that Pauli did make errors, such as predicting in a famous 4 December 1930 letter that the neutrino has the mass of the electron!]
To explain the mainstream spin-2 graviton idea, any particle having spin-2 will look identical after a 180 degree rotation in physical space, which will return the particle to its original form: a spin-n particle needs to be rotated by 360/n degrees to be returned to its original state. The spin of a particle dictates whether it obeys Bose-Einstein statistics (applies to bosons, i.e. where n is an integer) which can condense together, or Fermi-Dirac statistics (applies to fermions, i.e. where n is a half-integer) which only pair up with opposite spins and can’t individually behave as bosons condense into the same state. However, when two half-integer fermions pair up together, either as individual free particles or as the single electrons bound to the outer orbit of atoms, the resulting pair of fermions behaves as a boson if they are both in exactly the same energy state: this happens for example to helium which has two electrons that together (paired up) behave as a zero-viscosity “superfluid” at very low temperatures, 2 Kelvin or less, where they both share exactly the same “ground” energy state with opposite spins, forming a bosonic composite particle (the so-called “Bose-Einstein condensate”). Similarly in superconductivity, two conduction electrons pair up to form a “Cooper pair” of electrons, which behaves like a Bose-Einstein condensate, moving with very little resistance!
- For spin-(1/2) particles such as electrons, the particle is like a Mobius strip loop (with a half a twist so that both surfaces on the strip are connected into one surface on the loop) and so it needs to be rotated by 720 degrees to be restored to its original form.
- For spin-1 particles such as photons, the particle is simple and needs only be rotated by 360 degrees to be returned to its original state.
- For spin-2 particles such as the mainstream stringy graviton idea, the particle needs to be rotated by only 180 degrees to be returned to its original state.
The idea is that when spin-2 gravitons are exchanged between 2 masses, A and B, those going from A to B will be in the same state as those going from B to A, because they are distinguished by only a 180 degree rotation, and this will make them look indistinguishable and will produce an always attractive force. However, as explained above, this idea neglects other masses in the universe, and requires extra spatial dimensions which can’t be observed, so that the compactification of the unobserved spatial dimensions can be achieved in a vast number of different ways, precluding any possibility of making falsifiable predictions.
Crackpotism and the spin-2 graviton of stringy theory
Regarding Pauli’s crackpot spin-2 graviton theory, Pauli also made an error in predicting the neutrino: he thought it had the mass of the electron! But being wrong was better than being ‘not-even-wrong’ like the stringy landscape of Witten and others. See Pauli’s original letter of 4 Dec 1930 predicting neutrinos: http://wwwlapp.in2p3.fr/neutrinos/aplettre.html
This is significant because string theorists often falsely claim that Pauli’s prediction of the neutrino was speculative or apparently uncheckable (notice that Pauli’s letter ends with by saying to the experimentalists: ‘dear radioactive people, look [test] and judge’]. Pauli’s evidence for predicting the neutrino (which he called the neutron before Chadwick used that word to name a different, really massive neutral particle in 1932) was beta decay. By 1930 the beta spectrum was known as well as the mass change during beta decay: the beta particle [on average] emitted only carries 30% of the energy emitted. Hence 70% [on average] must be carried by a so-far unobserved particle. By conservation of energy, angular momentum and charge, Pauli could predict its properties.
Feynman explains that there was only one rival explanation to the neutrino on p. 75 of his book The Character of Physical Law (Penguin, London, 1992):
‘Two possibilities existed. … it was proposed by Bohr for a while that perhaps the conservation law worked only statistically, on the average. But it turns out now that the other possibility is the correct one … there is something else coming out [besides a beta particle], something which we now call an anti-neutrino.’
This isn’t like the landscape of 10500 vacua ‘predicted’ by the speculations of string theory. Apart from neutrinos, quarks and atoms are claimed by string theorists as examples of stringy-type speculative predictions with no evidence behind them. But was scientific evidence for quarks from the fact that the electrically neutral neutron has a magnetic moment from its spin (indicating that it contains electric charges) and from the SU(3) symmetry of hadron properties, and SU(3) symmetry correctly made predictions such as the omega-minus meson. For atoms, see Glasstone’s Sourcebook on Atomic Energy, Van Nostrand, 2nd ed., London, 1958, p. 2:
‘… Dalton made the theory quantitative … The atomic theory of the classical thinkers was somewhat in the nature of a vague philosophical speculation, but the theory as enunciated by Dalton … acted as a guide to further experimentation …’
DISCUSSION OF STRINGY SPIN-2 GRAVITON AND STRING THEORY AT http://blogs.discovermagazine.com/cosmicvariance/2007/05/24/string-theory-not-dead-yet/
‘I hear this “string theory demands the graviton” thing a lot, but the only explanation I’ve seen is that it predicts a spin-2 particle.’ – Rob Knop, May 24th, 2007 at 12:37 pm, http://blogs.discovermagazine.com/cosmicvariance/2007/05/24/string-theory-not-dead-yet/#comment-28901
‘A massless spin 2 particle is pretty much required to be a graviton by some results that go back to Feynman, I think.’ – String theorist Aaron Bergman, May 24th, 2007 at 12:44 pm, http://blogs.discovermagazine.com/cosmicvariance/2007/05/24/string-theory-not-dead-yet/#comment-28902 (Actually Richard P. Feynman points out in The Feynman Lectures on Gravitation, page 30, that gravitons do not have to be spin-2, which has not been observed.)
‘Rob, in addition to all the excellent reasons why a massless spin 2 particle must be the graviton, there are also explicit calculations demonstrating that forgone conclusion …’ – Moshe, May 24th, 2007 at 2:12 pm, http://blogs.discovermagazine.com/cosmicvariance/2007/05/24/string-theory-not-dead-yet/#comment-28891
‘Aaron Bergman wrote: ‘A massless spin 2 particle is pretty much required to be a graviton by some results that go back to Feynman, I think.’
‘Hmm. That sounds like a “folk theorem”: a theorem without assumptions, proof or even a precise statement.
‘Whatever these results are, they need to have extra assumptions. … Well, you can write down lots of ways a spin-2 particle can interact with other fields. Most of these have nothing to do with gravity. A graviton has got to interact with every other field — and in a very specific way.
‘Of course, most of these ways give disgusting quantum field theories that probably don’t make sense: they’re nonrenormalizable.
‘But, so is gravity!
‘So, it would be interesting to look at the results you’re talking about, and see what they actually say. Maybe the Einstein-Hilbert action is the “least nonrenormalizable” way for a spin-2 particle to interact with other particles… whatever that means?’ – Professor John Baez, May 25th, 2007 at 10:55 am, http://blogs.discovermagazine.com/cosmicvariance/2007/05/24/string-theory-not-dead-yet/#comment-28868
‘B writes: ‘The spin 2 particle can only couple to the energy-momentum tensor – as gravity does.’
Oh? Why?’ – Professor John Baez, May 25th, 2007 at 12:23 pm, http://blogs.discovermagazine.com/cosmicvariance/2007/05/24/string-theory-not-dead-yet/#comment-28878
‘…the point is that the massless spin-2 field is described by a symmetric two-index [rank-2] tensor with a certain gauge symmetry. … So its source must be a symmetric divergenceless two-index tensor. Basically you don’t have that many of them lying around, although I don’t know the rigorous statement to that effect.’ – Professor Sean Carroll, May 25th, 2007 at 12:31 pm, http://blogs.discovermagazine.com/cosmicvariance/2007/05/24/string-theory-not-dead-yet/#comment-28879
Dr Christine Dantas then draws attention at http://egregium.wordpress.com/2007/05/24/is-there-more-to-gravity-than-gravitons/ to the following paper:
T. Padmanabhan, ‘From Gravitons to Gravity: Myths and Reality’, http://arxiv.org/abs/gr-qc/0409089. which states on page 1:
‘There is a general belief, reinforced by statements in standard textbooks, that: (i) one can obtain the full non-linear Einstein’s theory of gravity by coupling a massless, spin-2 field hab self-consistently to the total energy momentum tensor, including its own; (ii) this procedure is unique and leads to Einstein-Hilbert action and (iii) it only uses standard concepts in Lorentz invariant field theory and does not involve any geometrical assumptions. After providing several reasons why such beliefs are suspect — and critically re-examining several previous attempts — we provide a detailed analysis aimed at clarifying the situation. First, we prove that it is impossible to obtain the Einstein-Hilbert (EH) action, starting from the standard action for gravitons in linear theory and iterating repeatedly. … Second, we use the Taylor series expansion of the action for Einstein’s theory, to identify the tensor Sab, to which the graviton field hab couples to the lowest order (through a term of the form Sabhab in the lagrangian). We show that the second rank tensor Sab is not the conventional energy momentum tensor Tab of the graviton and provide an explanation for this feature. Third, we construct the full nonlinear Einstein’s theory with the source being spin-0 field, spin-1 field or relativistic particles by explicitly coupling the spin-2 field to this second rank tensor Sab order by order and summing up the infinite series. Finally, we construct the theory obtained by self consistently coupling hab to the conventional energy momentum tensor Tab order by order and show that this does not lead to Einstein’s theory.’
Now we will check a predictive proof of the acceleration of the universe which originated before the observation that the universe is accelerating, a = Hc.
Notice that the outward acceleration of repulsion is opposed by the inward acceleration due to attraction of gravity, so the data is showing an absence of acceleration. Because cosmologists knew from the Friedmann metric of general relativity that the recession should be slowing down (expansion should be decelerating) at large distances, the absence of that deceleration implied the presence of an acceleration. Thus, as Nobel Laureate Phil Anderson says, the observed fact regarding the imaginary cosmological constant and dark energy is merely that:
“… the flat universe is just not decelerating, it isn’t really accelerating …”
– http://cosmicvariance.com/2006/01/03/danger-phil-anderson
This flat spacetime occurs where the outward acceleration of the universe offsets the inward acceleration due to gravitational acceleration, making spacetime flat (no acceleration/’curvature’). However, this balance with exactly flat spacetime only applies to receding matter at a particular distance from us (a few thousand million light years): for bigger distances than that, the cosmological acceleration exceeds gravitation and those receding objects have a net acceleration.
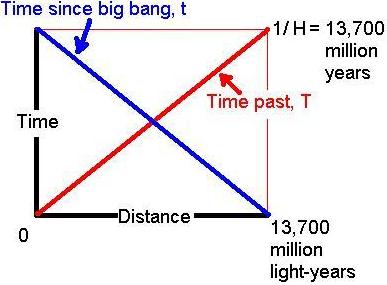
Fig. 2 – the basis of the Hubble acceleration. This figure comes from a previous post, here. But now I will add some clarifying comments about it. The diagram distinguishes the time since the big bang (which from our perspective on the universe is about 13,700 million years) from the time past that we see when we look to greater distances due to the delay caused by the transit time of the light radiation in its propagation to us observers here on Earth from a large distance. It’s best to build physical models upon directly observed facts like the Hubble recession law, not upon speculative metrics of general relativity which firstly is only at best an approximation to quantum gravity (which will differ from general relativity because quantum field gravitons will be subject to redshift when exchanged between receding masses in the expanding universe), and secondly depends on indirect observations such as theories of unobserved dark matter and unobserved dark energy to overcome observational anomalies. The observed Hubble recession law states that recession v = HR, where R = cT, T being time past (when the light was emitted), not the time after the big bang for the Earth.
As shown in Fig. 2, this time past T is related to time since the big bang t for the distance of the star in question by the simple expression: t + T = 1/H, for flat spacetime as has been observed since 1998 (the observed acceleration of the universe cancels gravitational deceleration of distant objects, so there is no curvature on large distance scales).
Hence:
v = HR = HcT = Hc[(1/H) – t] = c – (Hct)
a = dv/dt = d[c – (Hct)]/dt = -Hc = 6×10-10 ms-2
which is cosmological acceleration of the universe (since observed to be reality, from supernova redshifts!). E.g., Professor Lee Smolin writes in the chapter ‘Surprises from the Real World’ in his 2006 book The Trouble with Physics: The Rise of String Theory, the fall of a Science, and What Comes next (Allen Lane, London), pages 209:
‘… c2/R [which for R = ct = c/H gives a = c2/(ct) = Hc, the result we derived theoretically in 1996, unlike Smolin’s ad hoc dimensional analysis numerology of 2006]… is in fact the acceleration by which the rate of expansion of the universe is increasing – that is, the acceleration produced by the cosmological constant.’
The figure 6×10-10 ms-2 is the outward acceleration which Smolin quotes as c2/R. Full credit to Smolin for actually stating what the acceleration of the universe was measured to be! There are numerous popular media articles, books and TV documentaries about the acceleration of the universe which are all so metaphysical they they don’t even state that it is measured to be 6 x 10-10 ms-2! On the next page, 210, Smolin however ignores my published prediction of the cosmological acceleration two years before its discovery and instead discusses an observation by Mordehai Milgrom who ‘published his findings in 1983, but for many years they were largely ignored’. Smolin explains that galactic rotation curves obey Newtonian gravitation near the middle of the galaxy and only require unobserved ‘dark matter’ near the outside: Milgrom found that the radius where Newtonian gravity broke down and required ‘dark matter’ assumptions was always where the gravitational acceleration was 1.2 x 10-10 ms-2, on the order of the cosmological acceleration of the universe. Smolin comments on page 210:
‘As long as the [centripetal] acceleration of the star [orbiting the centre of a galaxy] exceeds this critical value, Newton’s law seems to work and the acceleration predicted [by Newton’s law] is the one seen. There is no need to posit any dark matter in these cases. But when the acceleration observed is smaller than the critical value, it no longer agrees with the prediction of Newton’s law.’
(The theoretical derivation of the acceleration we have given above is valid for all matter regardless of distance, but as we have noted there is a mechanism involved and gravitons only produce repulsive acceleration where the masses are extremely large, but in some cases this could influence the galactic rotation curves where the centripetal accelerations involved are of the same order of magnitude as the cosmological acceleration. Milgrom’s 1983 ‘Modified Newtonian Dynamics (MOND)’ claimed that Newton’s law only holds down to values of a = MG/r2 = 1.2 x 10-10 ms-2, and for lower accelerations he thought that the gravity acceleration fell only inversely as the distance rather than as the inverse square law. This would get rid of the need for dark matter. But the actual law including cosmological acceleration may be like a = (MG/r2) – (Hc) where the cosmological repulsive acceleration Hc is given a minus sign because it acts in the opposite direction to gravitational attraction.)
This is a simple result obtained in May 1996 and published via Electronics World in October 1996 (journals like Classical and Quantum Gravity and Nature censored it because it leads to a quantum gravity theory which is different to mainstream-defended string theory, which makes checkable predictions and survives tests unlike mainstream-defended string theory). It was only in 1998 that Dr Saul Perlmutter finally made the discovery using CCD telescopes that yes, indeed, the universe is accelerating as predicted in May 1996, although for an obvious reason (ignorance) he did not refer to the prediction made earlier! The editors of Nature, which published Perlmutter, again in 1998 onwards have refused to publish the fact that the observation confirmed the earlier prediction! This is the problem with the scientific method: the politics of censorship ban radical advances. Relevant to this fact is Professor Freeman Dyson’s observation in his 1981 essay Unfashionable Pursuits (quoted by Tony Smith):
‘… At any particular moment in the history of science, the most important and fruitful ideas are often lying dormant merely because they are unfashionable. Especially in mathematical physics, there is commonly a lag of fifty or a hundred years between the conception of a new idea and its emergence into the mainstream of scientific thought. If this is the time scale of fundamental advance, it follows that anybody doing fundamental work in mathematical physics is almost certain to be unfashionable. …’
‘… My way of looking at things was completely new, and I could not deduce it from other known mathematical schemes, but I knew what I had done was right. … For instance, take the exclusion principle … it turns out that you don’t have to pay much attention to that in the intermediate states in the perturbation theory.
‘I had discovered from empirical rules that if you don’t pay attention to it, you get the right answers anyway …. Teller said: “… It is fundamentally wrong that you don’t have to take the exclusion principle into account.” … Dirac asked “Is it unitary?” … Dirac had proved … that in quantum mechanics, since you progress only forward in time, you have to have a unitary operator. But there is no unitary way of dealing with a single electron. Dirac could not think of going forwards and backwards … in time … Bohr … said: “… one could not talk about the trajectory of an electron in the atom, because it was something not observable.” … Bohr thought that I didn’t know the uncertainty principle … I gave up, I simply gave up …”.’ (The Beat of a Different Drum: The Life and Science of Richard Feynman, by Jagdish Mehra, Oxford University Press, 1994, pp. 245-248.)
Teller dismissed Feynman’s work because it ignored the exclusion principle, Dirac dismissed it because it didn’t have a unitary operator to make the sum of probabilities for all alternatives always equal to 1 (only the final result of the path integral was normalized to a total probability of 1, so that only one electron arrives at say the screen in the double slit experiment: clearly the whole basis of the path integral seems to violate unitary for intermediate times when the electron is supposed to take all paths like an infinite number of particles, and thus interfere with ‘itself’ before arriving – as a single particle on the screen!), and Bohr dismissed it because he claimed Feynman didn’t know the uncertainty principle, and claimed that the uncertainty principle dismissed any notion of path integrals representing the trajectory of an electron!
As a result of such dismissive peer-review, Feynman’s brilliant paper reformulating quantum field theory, ‘Space-Time Approach to Non-Relativistic Quantum Mechanics’, was actually rejected for publication by the Physical Review (see http://arxiv.org/PS_cache/quant-ph/pdf/0004/0004090v1.pdf page 2) before finally being published instead by Reviews of Modern Physics (v. 20, 1948, p. 367).
Feynman concluded: ‘… it didn’t make me angry, it just made me realize that … [ they ] … didn’t know what I was talking about, and it was hopeless to try to explain it further. I gave up, I simply gave up …”.’ (The Beat of a Different Drum: The Life and Science of Richard Feynman, by Jagdish Mehra, Oxford University Press, 1994, pp. 245-248.)
Feynman in 1985 in his book QED explained clearly in a footnote that the uncertainty principle is not a separate law from path integrals so Bohr’s objection was invalid; interferences due to the random virtual photon exchanges between the charges in the atom – which cause the non-classical Coulomb force – cause the uncertainty in the position of an electron within an atom!
But if this kind of ignorant dismissal and rejection from numerous top ‘experts’ can happen to Feynman’s path integrals, it surely can happen to any radical-enough-to-be-helpful quantum gravity ideas! Consequently, Feynman denounced such ‘expert’ opinion/belief when it is not based on facts:
‘Science is the organized skepticism in the reliability of expert opinion.’ – R. P. Feynman (quoted by Smolin, The Trouble with Physics, 2006, p. 307).
‘Science is the belief in the ignorance of experts.’ – R. P. Feynman, The Pleasure of Finding Things Out, 1999, p. 187.
Teller, Dirac and Bohr had a very easy job dismissing Feynman’s path integrals; they simply picked out bits of his work they couldn’t grasp, falsely declared those bits to be wrong or nonsense, and then ignored the rest!
Against this kind of unconstructive ‘criticism’ [do you really suffer a ‘criticism’ if someone falsely attacks you and uses their prestige to silence you from making any reply or defending yourself against their ignorant assertions, or are they really the ones who are making fools of themselves? – the answer to this will depend on whether there are any bystanders of influence and if they can grasp the facts or are duped, or unwilling/unable to help science], Feynman didn’t see any point in responding. If the egos of other people prevent them from taking a real interest in your work, if those other people have more to gain to their already massive egos by dismissing little people than by listening to those they consider to be little people, what is the point in trying to talk to them? You would need to be a politician to diplomatically nurture their egos enough to get them to invest a moment in your advance. They won’t do it willingly; they don’t do it for the sake of physics. They live in a string community that they call physics, a community which exists to offer help and assistance to group members, which believes in speculative groupthink and isn’t concerned with factual predictions that have been confirmed, and which seeks to defend itself and seek status by attacking others.
Professor Freeman Dyson in a dramatic interview on Google Video explains how in addition to the nonsensical egotistical ‘objections’ by Teller, Dirac and Bohr, the famous physicist Oppenheimer also tried to destroy Dyson’s efforts to explain Feynman’s work, using the tactic of meaningless, rude interruptions to his lecture.
Above: Dyson explains how leading physicist Oppenheimer was a ‘bigoted old fool’ in egotistically sneering at the wording of new ideas and refusing to listen to new ideas outside his area of interest. Dyson and Bethe had to struggle to get him to listen, in order to get Feynman’s work taken seriously. Without the eventual backing of Oppenheimer, it would have remained hidden from mainstream attention. [This is quite common mainstream methodology to secure continued attention by stamping on alternative ideas, contrary to the claim certain string theorists make that there would be an overnight scientific revolution if only someone came up with a theory of quantum gravity that works better than string theory – see the comments section of this post.]
Just to add another example, apart from Feynman’s path integral, of an idea which is now central to quantum field theory yet which started off being ridiculed and objected to, take Yang-Mills theory which is central to the Standard Model of particle physics! In this case, Pauli objected to C. N. Yang’s presentation of the Yang-Mills theory at Princeton in February 1954 so strongly that Yang had to stop and sit down, although – to give the devil his due – Oppenheimer was more reasonable at that time, and encouraged Yang to continue his lecture. Yang writes:
‘Wolfgang Pauli (1900-1958) was spending the year in Princeton, and was deeply interested in symmetries and interactions…. Soon after my seminar began … Pauli asked, “What is the mass of this field …?” I said we did not know. Then I resumed my presentation but soon Pauli asked the same question again. I said something to the effect that it was a very complicated problem, we had worked on it and had come to no definite conclusions.
‘I still remember his repartee: “That is not sufficient excuse”. I was so taken aback that I decided, after a few moments’ hesitation, to sit down. There was general embarrassment. Finally Oppenheimer said, “We should let Frank proceed”. I then resumed and Pauli did not ask any more questions during the seminar.’
This episode is somewhat reminiscent of Samuel Cohen’s account of Oppenheimer’s own behaviour at Los Alamos when a nervous physicist – Dick Erlich – was trying to give a lecture:
‘On another occasion, to expose another side of Oppenheimer’s personality, which could be intolerant and downright sadistic, he showed up at a seminar to hear Dick Erlich, a very bright young physicist with a terrible stuttering problem, which got even worse when he became nervous. Poor Dick, who was having a hard enough time at the blackboard explaining his equations, went into a state of panic when Oppenheimer walked in unexpectedly. His stuttering became pathetic, but with one exception everyone loyally stayed on trying to decipher what he was trying to say. This exception was Oppenheimer, who sat there for a few minutes, then got up and said to Dick: “You know, we’re all cleared to know what you’re doing, so why don’t you tell us.” With that he left, leaving Dick absolutely devastated and unable to continue. Also devastated were the rest of us who worshipped Oppenheimer, for very good reasons, and couldn’t believe he could act so cruelly.’
– S. Cohen, ‘F— You! Mr. President: Confessions of the Father of the Neutron Bomb’, 3rd Edition, 2006, page 24.
Path integrals for fundamental forces in quantum field theory
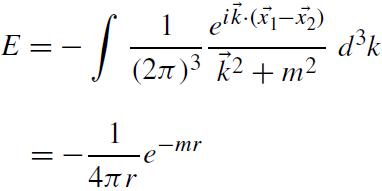
Above: the path integral performed for the Yukawa field, the simplest system in which the exchange of massive virtual pions between two nucleons causes an attractive force. Virtual pions will exist all around nucleons out to a short range, and if two nucleons get close enough for their virtual pion fields to overlap, they will be attracted together. This is a little like Lesage’s idea where massive particles push charges together over a short range (the range being limited by the diffusion of the massive particles into the ‘shadowing’ regions). (See page 26 of Zee for discussion, and page 29 for integration technique. But we will discuss the components of this and other path integrals in detail below.) Zee comments on the result above on page 26: “This energy is negative! The presence of two … sources, at x1 and x2, has lowered the energy. In other words, two sources attract each other by virtue of their coupling to the field … We have derived our first physical result in quantum field theory.” This 1935 Yukawa theory explains the strong nuclear attraction between nucleons in a nucleus by predicting that the exchange of pions (discovered later with the mass Yukawa predicted) would overcome the electrostatic repulsion between the protons, which would otherwise blow the nucleus apart.
But the way the mathematical Yukawa theory has been generalized to electromagnetism and gravity is the basic flaw in today’s quantum field theory: to analyze the force between two charges, located at positions in space x1 and x2, the path integral is done including only those two charges, and just ignoring the vast number of charges in the rest of the universe which – for infinite range inverse-square law forces – are also exchanging virtual gauge bosons with x1 and x2!
A potential energy which varies inversely with distance implies a force which varies as the inverse-square law of distance, because work energy W = Fr, where force F acts over distance r, hence F = W/r, and since energy W is inversely proportional to r, we get F ~ 1/r2. (Distances x in the integrand result in the radial distance r in the result for potential energy above.) In the case of gravity and electromagnetism, the effective mass of the gauge boson in this equation m ~ 0, which gets rid of the exponential term (spin-2 gravitons are supposed to have mass to enable graviton-graviton interactions to enhance the strength of the graviton interaction at high energy in strong fields enough to “unify” the strength of gravity with standard model forces near the Planck scale – an assumption about “unification” which is physically in error (see Figures 1 and 2 in the blog post https://nige.wordpress.com/2007/07/17/energy-conservation-in-the-standard-model/) – and additionally, we’ve shown why spin-2 gravitons are based on error and anyway in the standard model all mass arises from an external vacuum “Higgs” field and is not intrinsic). The exponential term is however important in the short-range weak and strong interactions. Weak gauge bosons are supposed to get their mass from some vacuum (Higgs) field, while massless gluons cause a pion-mediated attraction of nucleons, where the pions have mass so the effective field theory for nuclear physics is of the Yukawa sort.
A path integral calculates the amplitude for an interaction which can occur by a variety of different possible paths through spacetime. The numerator of the path integral integrand above is derived from the phase factor, representing the relative amplitude of a particular path, is simply the exponential term e–iHT = eiS where H is the Hamiltonian (which for the free-particle of mass m is simply representing kinetic energy of the particle, H = E = p2/(2m) = (1/2)mv2; in the event of there being a force-field present, the Hamiltonian must subtract the potential energy V, due to the force field, from the kinetic energy: H = p2/(2m) – V), T is time, and S is the action for the particular path measured in quantum action units of h-bar (the action S is the integral of the Lagrangian field equation over time for a particular path, S = òL dt).
The origin of the phase factor for the amplitude of a particular path, e–iHT, is simply the time-dependent Schroedinger equation of quantum mechanics: i{h-bar}d{Psi}/dt = H, where H is the Hamiltonian (energy operator). Solving this gives wavefunction amplitude, {Psi} = e–iHT/h-bar, or simply e–iHT if we express HT in units of h-bar. Behind the mathematical symbolism, it’s extremely simple physics, just being a description of the way that waves can reinforce if in phase and adding together, or cancel out if they are out of phase.
The denominator of the path integral integrand above is derived from the propagator, D(x), which Zee on page 23 describes as being: ‘the amplitude for a disturbance in the field to propagate from the origin to x.’ This amplitude for calculating a fundamental force using a path integral is constructed using Feynman’s basic rules for conservation of momentum (see page 53 of Zee’s 2003 QFT textbook).
1. Draw the Feynman diagram for the basic process, e.g. a simple tree diagram for Møller scattering of electrons via the exchange of virtual photons.
2. Label each internal line in the diagram with a momentum k and associate it with the propagator i/(k2 – m2 + ie). (Note that when k2 = m2, momentum k is “on shell” and is the momentum of a real, long-lived particle, but k can also take many values which are “off shell” and these represent “virtual particles” which are only indirectly observable from the forces they produce. Also note that ie is infinitesimal and can be dropped where k2 – m2 is positive, see Zee page 26.)
3. Associate each interaction vertex with the appropriate coupling constant for the type of fundamental interaction (electromagnetic, weak, gravitational, etc.) involved, and set the sum of the momentum going into that vertex equal to the sum of the momentum going out of that vertex.
4. Integrate the momentum associated with internal lines over the measure d4k/(2p)4.
Clearly, this kind of procedure is feasible when a few charges are considered, but is not feasible at step 1 when you have to include all the charges in the universe! The Feynman diagram would be way too complicated if trying to include 1080 charges, which is precisely why we have used geometry to simplify the graviton exchange path integral when including all the charges in the universe.
Zee gives some interesting physical descriptions of the way that forces are mediated by the exchange of virtual photons (which seem to interact in some respects like real photons scattering off charges to impart forces, or being created at a charge, propagating to another charge, being annihilated on absorption by that charge, with a fresh gauge boson then being created and propagating back to the first charge again) on pages 20, 24 and 27:
“Somewhere in space, at some instant in time, we would like to create a particle, watch it propagate for a while, then annihilate it somewhere else in space, at some later instant in time. In other words, we want to create a source and a sink (sometimes referred to collectively as sources) at which particles can be created and annihilated.” (Page 20.)
“We thus interpret the physics contained in our simple field theory as follows: In region 1 in spacetime there exists a source that sends out a ‘disturbance in the field’, which is later absorbed by a sink in region 2 in spacetime. Experimentalists choose to call this disturbance in the field a particle of mass m.” (Page 24.)
“That the exchange of a particle can produce a force was one of the most profound conceptual advances in physics. We now associate a particle with each of the known forces: for example, the [virtual, 4-polarizations] photon with the electromagnetic force, and the graviton with the gravitational force; the former is experimentally well established [virtual photons push measurably nearby metal plates together in the Casimir effect] and the latter, while it has not yet been detected experimentally, hardly anyone doubts its existence. We … can already answer a question smart high school students often ask: Why do Newton’s gravitational force and Coulomb’s electric force both obey the 1/r2 law?
“We see from [E = -(e–mr)/(4pr)] that if the mass m of the mediating particle vanishes, the force produced will obey the 1/r2 law.” (Page 27.)
The problem with this last claim Zee makes is that mainstream spin-2 gravitons are supposed to have mass, so gravity would have a limited range, but this is a trivial point in comparison to the errors already discussed in mainstream (spin-2 graviton) approaches to quantum gravity. Zee in the next chapter, Chapter I.5 “Coulomb and Newton: Repulsion and Attraction”, gives a slightly more rigorous formulation of the mainstream quantum field theory for electromagnetic and gravitational forces, which is worth study. It makes the same basic error as the 1935 Yukawa theory, in treating the path integral of gauge bosons between only the particles upon which the forces appear to act, thus inaccurately ignoring all the other particles in the universe which are also contributing virtual particles to the interaction!
Because of the involvement of mass with the propagator, Zee uses a trick from Sidney Coleman where you work through the electromagnetic force calculation using a photon mass m and then set m = 0 at the end, to simplify the calculation (to avoid dealing with gauge invariance). Zee then points out that the electromagnetic Lagrangian density L = -(1/4)FmnFmn (where Fmn = 2dAmn = dmAn – dnAm, Am(x) being the vector potential) has an overall minus sign in the Lagrangian so that action is lost when there is a variation in time! Doing the path integral with this negative Lagrangian (with a small mass added to the photon to make the field theory work) results in a positive sign for the potential energy between two lumps of similar charge, so: “The electromagnetic force between like charges is repulsive!” (Zee, page 31.)
This is quite impressive and tells us that the quantum field theory gives the right result without fiddling in this repulsion case: two similar electric charges exchange gauge bosons in a relatively simple way with one another, and this process, akin to people firing objects at one another, causes them to repel (if someone fires something at you, they are forced away from you by the recoil and you are knocked away from them when you are hit, so you are both forced apart!). Notice that such exchanged virtual photons must be stopped (or shielded) by charges in order to impart momentum and produce forces! Therefore, there must be an interaction cross-section for charges to physically absorb (or scatter back) virtual photons, and this fact offers a simple alternative formulation of the Coulomb force quantum field theory using geometry instead of path integrals!
Zee then goes on to gravitation, where the problem – from his perspective – is how to get the opposite result for two similar-sign gravitational charges than you get for similar electric charges (attraction of similar charges, not repulsion!). By ignoring the fact that the rest of the mass in the universe is of like charge to his two little lumps of energy, and so is contributing gravitons to the interaction, Zee makes the mainstream error of having to postulate a spin-2 graviton for exchange between his two masses (in a non-existent, imaginary empty universe!) just as Fierz and Pauli had suggested back in 1939.
At this point, Zee goes into fantasy physics, with a spin-2 graviton having 5 polarizations being exchanged between masses to produce an always attractive force between two masses, ignoring the rest of the mass in the universe.
It’s quite wrong of him to state on page 34 that because a spin-2 graviton Lagrangian results in universal attraction for a totally false, misleading path integral of graviton exchange between merely two masses, “we see that while like [electric] charges repel, masses [gravitational charges] attract.” This is wrong because even neglecting the error I’ve pointed out of ignoring gravitational charges (masses) all around us in the universe, Zee has got himself into a catch 22 or circular argument: he first assumes the spin-2 graviton to start off with, then claims that because it would cause attraction in his totally unreal (empty apart from two test masses) universe, he has explained why masses attract. However, the only reason why he assumes a spin-2 graviton to start off with is because that gives the desired properties in the false calculation! It isn’t an explanation. If you assume something (without any physical evidence, such as observation of spin-2 gravitons) just because you already know it does something in a particular calculation, you haven’t explained anything by then giving that calculation which merely is the basis for the assumption you are making! (By analogy, you can’t pull yourself up in the air by tugging at your bootstraps.)
This perversion of physical understanding gets worse. On page 35, Zee states:
“It is difficult to overstate the importance (not to speak of the beauty) of what we have learned: The exchange of a spin 0 particle produces an attractive force, of a spin 1 particle produces a repulsive force, and of a spin 2 particle an attractive force, realized in the hadronic strong interaction, the electromagnetic interaction, and the gravitational interaction, respectively.”
Notice the creepy way that the spin-2 graviton – completely unobserved in nature – is steadily promoted in stature as Zee goes through the book, ending up the foundation stone of mainstream physics, string theory:
‘String theory has the remarkable property of predicting [spin-2] gravity.’ – Professor Edward Witten (M-theory originator), ‘Reflections on the Fate of Spacetime’, Physics Today, April 1996.
“For the last eighteen years particle theory has been dominated by a single approach to the unification of the Standard Model interactions and quantum gravity. This line of thought has hardened into a new orthodoxy … It is a striking fact that there is absolutely no evidence whatsoever for this complex and unattractive conjectural theory. There is not even a serious proposal for what the dynamics of the fundamental ‘M-theory’ is supposed to be or any reason at all to believe that its dynamics would produce a vacuum state with the desired properties. The sole argument generally given to justify this picture of the world is that perturbative string theories have a massless spin two mode and thus could provide an explanation of gravity, if one ever managed to find an underlying theory for which perturbative string theory is the perturbative expansion.” [Emphasis added.]
– Dr Peter Woit, http://arxiv.org/abs/hep-th/0206135, page 52.
The consequence of Witten’s spin-2 graviton mindset (adopted by string theorists without any reservations) is that when I submitted a paper to Classical and Quantum Gravity ten years ago (by post), the editor sent it for ‘peer-review’ and received a rejection decision by an anonymous ‘referee’ which he forwarded to me, just ignorant attack which ignored the physics altogether and just claimed it was wrong because it didn’t connect with the spin-2 graviton of string theory!
Sent: 02/01/03 17:47
Subject: Your_manuscript LZ8276 Cook
Physical Review Letters does not, in general, publish papers on alternatives to currently accepted theories.
Yours sincerely,
Stanley G. Brown, Editor,
Physical Review Letters
Now, why has this nice genuine guy still not published his personally endorsed proof of what is a “currently accepted” prediction for the strength of gravity? Will he ever do so?
“… in addition to the dimensionality issue, the string theory approach is (so far, in almost all respects) restricted to being merely a perturbation theory.”
– Sir Roger Penrose, The Road to Reality, Jonathan Cape, London, 2004, page 896.
Richard P. Feynman points out in The Feynman Lectures on Gravitation, page 30, that gravitons do not have to be spin-2, which has never been observed! Despite this, the censorship of the facts by mainstream “stringy” theorists persists:
nigel says:
February 24, 2006 at 5:26 amhttp://arxiv.org/help/endorsement –
‘We don’t expect you to read the paper in detail, or verify that the work is correct, but you should check that the paper is appropriate for the subject area. You should not endorse the author … if the work is entirely disconnected with current [string theory] work in the area.’
They don’t want any really strong evidence of dissent. This filtering means that the arxiv reflects pro-mainstream bias. It sends out a powerful warning message that if you want to be a scientist, don’t heckle the mainstream or your work will be deleted.
In 2002 I failed to get a single brief paper about a crazy-looking yet predictive model on to arxiv via my university affiliation (there was no other endorsement needed at that time). In emailed correspondence they told me to go get my own internet site if I wasn’t contributing to mainstream [stringy] ideas.
Now let’s examine what Feynman (1918-88) says about this mechanism. In November 1964, the year before receiving the Nobel Prize for path integrals, Feynman gave a series of lectures at Cornell University on ‘The Character of Physical Law’, which were filmed by the BBC for transmission on BBC2 TV in 1965. The transcript has been published as a book by the BBC in 1965 and MIT press in 1967, ‘The Character of Physical Law,’ and is still in print as a publication of Penguin Books in England.
I’ll discuss the Penguin Books edition. In the first lecture, The Law of Gravitation, an example of Physical Law, Feynman explains that Kepler [1571-1630, the discoverer of the three laws of planetary motion and assistant to Brahe] used the heuristic scientific method – trial and error – to discover the way planets go around the sun, saying on page 16:
‘At one stage he thought he had it … they went round the sun in circles with the sun off centre. Then Kepler noticed that … Mars was eight minutes of arc off, and he decided that this was too big for Tycho Brahe [1546-1601, the astronomer who collected Kepler’s data] to have made an error, and that this was not the right answer. So because of the precision of the experiments, he was able to proceed to another trial and ultimately found out three things. … the planets went in ellipses around the sun with the sun as a focus. … the area that is enclosed in the orbit of the planet and the two lines [from sun to planet] that are separated by the planet’s position three weeks apart is the same, in any part of the orbit. So that the planet has to go faster when it is closer to the sun, and slower when it is farther away, in order to show precisely the same area [equal areas are swept out in equal times].
‘Some several years later, Kepler found a third rule … It said that the time the planet took to go all around the sun … varied as the square root of the cube of the size of the orbit and for this the size of the orbit is the diameter across the biggest distance on the ellipse.’
These laws allowed Hooke and Newton to formulate the inverse-square law of gravity. They knew the Moon is 60 times as far from the centre of the Earth as an observer on the surface of the earth is, so Earth’s field of acceleration due to gravity is 60*60 = 3,600 times weaker at the Moon than at the Earth’s surface. Hence the acceleration needed to keep the Moon in its orbit, equal to a = v2/r (the square of its orbital speed divided by the distance of the Moon from the centre of the Earth) = 0.003 ms-2 should be 3,600 times weaker than the acceleration due to gravity measured by Galileo on Earth’s surface. Since the result was correct, the inverse square law calculated from Kepler’s laws for planetary motion had been extended from the solar system to falling apples here on the Earth!
At the end of that first lecture, The Law of Gravitation, an example of Physical Law, Feynman says: ‘You will say to me, “Yes, you told us what happens, but what is gravity? Where does it come from? What is it? Do you mean to tell me that a planet looks at the sun, sees how far it is, calculates the inverse square of the distance and then decides to move in accordance with that law?” In other words, although I have stated the mathematical law, I have given no clue about the mechanism. I will discuss the possibility of doing this in the next lecture, The relation of mathematics to physics.
‘In this lecture I would like to emphasize, just at the end, some characteristics that gravity has in common with the other laws … it is mathematical in its expression … it is not exact; Einstein had to modify it, and we know it is not quite right yet, because we have still to put the quantum theory in. That is the same with all our laws – they are not exact.’
(This is the opposite of Eugene Wigner’s false claim in 1960 about the ‘unreasonable effectiveness of mathematics in the physical sciences’ that implicitly suggests that mathematics surprisingly provides a perfect, totally accurate description of nature! Wigner had the job of designing the large-scale plutonium reactors in World War II for nuclear weapons production. When the engineers deliberately increased the reactor core size so that it could hold additional uranium, Wigner was extremely offended and actually threatened to resign, complaining that the engineers didn’t understand how precise the nuclear physics measurements and calculations were. But it turned out that the reactor wouldn’t operate without a lot more uranium because the measurements and calculations were useless: they didn’t include the effect of the gradual build-up over a few hours in a high flux reactor of fission products that absorbed a lot of the neutron flux! So the mathematical physics as wielded by Wigner was wrong, and the cynical engineers were right not to trust the accuracy estimates of Wigner’s calculations. Feynman, who worked applying computers to test bomb designs in the Manhattan Project, was well aware of this lesson from trying to use mathematical laws in the real world: see his signature on the last page of this copy of the Los Alamos Handbook of Nuclear Physics, LA-11)
In the second lecture, The Relation of Mathematics to Physics, Feynman questions how deep the mathematical basis of physical law goes. He starts with the example of Faraday’s law of electrolysis, which states that the amount of material electroplated is proportional to the current and the time the current flows for. He points out that this means that the amount of matter plated by electricity is just proportional to the total charge that flows, and since each atom needs 1 electron to come to be deposited, the physical mechanism behind the law is easy to understand: it is not a mathematical mystery.
Then he moves on to gravity on page 37:
‘What does the planet do? Does it look at the sun, see how far away it is, and decide to calculate on its internal adding machine the inverse of the square of the distance, which tells it how much to move? This is certainly no explanation of the machinery of gravitation! You might want to look further, and various people have tried to look further.
‘… I would like to describe one theory which has been invented, among others, of the type you might want. This theory suggests that this effect of large numbers of actions, which would explain why it is mathematical.
‘Suppose that in the world everywhere there are a lot of particles, flying through us at very high speed. They come equally in all directions – just shooting by – and once in a while they hit us in a bombardment. We, and the sun, are practically transparent for them, practically but not completely, and some of them hit. Look, then, at what would happen.
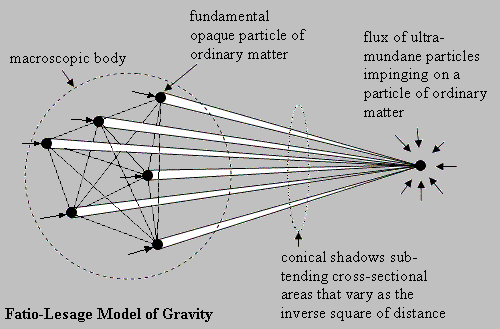 [Illustration credit: http://www.mathpages.com/HOME/kmath131/kmath131.htm]
[Illustration credit: http://www.mathpages.com/HOME/kmath131/kmath131.htm]
‘If the sun were not there, particles would be bombarding the Earth from all sides, giving little impulses by the rattle, bang, bang of the few that hit. This will not shake the Earth in any particular direction, because there are as many coming from one side as from the other, from top as from bottom.
‘However, when the sun is there the particles which are coming from that direction are partly absorbed [or reflected, as in the case of Yang-Mills gravitons, an exchange radiation!] by the sun, because some of them hit the sun and do not go through. Therefore, the number coming from the sun’s direction towards the Earth is less than the number coming from the other sides, because they meet an obstacle, the sun. It is easy to see that the farther the sun is away, of all the possible directions in which particles can come, a smaller proportion of the particles are being taken out.
‘The sun will appear smaller – in fact inversely as the square of the distance. Therefore there will be an impulse on the Earth towards the sun that varies inversely as the square of the distance. And this will be a result of large numbers of very simple operations, just hits, one after the other, from all directions. Therefore the strangeness of the mathematical relation will be very much reduced, because the fundamental operation is much simpler than calculating the inverse square of the distance. This design, with the particles bouncing, does the calculation.
‘The only trouble with this scheme is that … If the Earth is moving, more particles will hit it from in front than from behind. (If you are running in the rain, more rain hits you in the front of the face than in the back of the head, because you are running into the rain.) So, if the Earth is moving it is running into the particles coming towards it and away from the ones that are chasing it from behind. So more particles will hit it from the front than from the back, and there will be a force opposing any motion. This force would slow the Earth up in its orbit… So that is the end of that theory.
‘”Well,’ you say, ‘it was a good one … Maybe I could invent a better one.’ Maybe you can, because nobody knows the ultimate. …
‘It always bothers me that, according to the laws as we understand them today, it takes a computing machine an infinite number of logical operations to figure out what goes on in no matter how tiny a region of space, and no matter how tiny a region of time. How can all that be going on in that tiny space? Why should it take an infinite amount of logic to figure out what one tiny piece of spacetime is going to do? So I have often made the hypothesis that ultimately physics will not require a mathematical statement, that in the end the machinery will be revealed, and the laws will turn out to be simple, like the chequer board with all its apparent complexities.’
The ‘drag’ force Feynman describes (in debunking the obsolete LeSage gas pressure mechanism) doesn’t slow down moving objects in any quantum field because the exchange radiation can’t continually carry away kinetic energy like a gas can. As we observe, it is only when an electron accelerates that it is able to radiate away waves which carry energy in the surrounding field, e.g. radio waves from accelerating charge, so fundamental charged particles only show a resistance to being accelerated (which takes away energy as radiation), not a continuously energy-losing drag that can slow down particles moving at steady velocity, and therefore the interaction due to the motion of a particle with the surrounding quantum field doesn’t cause continuous drag, but instead is actually the mechanism of inertia (resistance to acceleration, i.e. the 1st law of motion) and the Fitzgerald-Lorentz contraction of bodies in the direction of their motion in space. Feynman’s objection doesn’t hold water; it it die it would discredit all quantum graviton theories and there would be no physical mechanism for inertia and the Lorentz-FitzGerald contraction, nor for the (1/3)MG/c2 = 1.5 mm contraction of the Earth’s radius (by graviton exchange pressure!) predicted by general relativity on the basis of conservation of energy in gravitational fields!
The FitzGerald-Lorentz contraction is demonstrated by the Michelson-Morley experiment and occurs whenever acceleration occurs, but remains constant if the velocity is constant. This radiation pressure effect is analogous to the contraction of length due to the compression of an aircraft or ship when moving nose or bow first head-on into air or water, although the graviton field behaves as a perfect, dragless fluid: massless gravitons travel at light velocity and don’t get speeded up like molecules of a massive gas carrying away energy and thus slowing down an object moving through a massive gas. There is a force on the front which tends to cause a small contraction that depends on the velocity. The report http://arxiv.org/abs/gr-qc/0011064 on page 3 shows how the FitzGerald-Lorentz contraction formula for gamma can result from head-on pressure when a charge is moving in the Dirac sea quantum field theory vacuum, citing C. F. Frank, Proceedings of the Physical Society of London, vol. A 62 (1949), pp. 131–134. For further details, see also the previous post on this blog, https://nige.wordpress.com/2007/07/04/metrics-and-gravitation/, plus the information in the comments following that post.
For emphasis: the Feynman ‘drag’ objection to a quantum field that causes gravity is bunk not just because of the contraction of moving bodies and the fact we know that charges only radiate (lose energy) in a field when accelerating, but also because we know quantum fields exist in space from the Casimir effect and other experiments. Reproducable, highly accurate quantum force experiments beyond a shadow of a doubt prove that quantum fields exist in space that produce forces without causing drag, other than a drag to accelerations (observed inertia, observed Lorentz-Fitzgerald contraction). There is therefore motion of charges in quantum fields without drag, because we see it without seeing drag! While it is good to seek theoretical objections to theories where there is some evidence that such objections are real, it is not sensible to keep clinging to an unobservable objection which simply doesn’t exist in the real world. There is no evidence that gauge boson fields cause drag, so drop the dead donkey. Motion in quantum virtual particle fields doesn’t slow down planets, tough luck if you wanted nature to behave differently. Because gravitons don’t slow things down, they don’t heat up the planets. So all the objections of Poincare that planets should be red hot from planets moving in the quantum field vacuum are bunk. No net energy flows into or out of the gravitational field unless the gravitational potential energy of a mass varies, which requires a force Fto do work E = F*x by moving the object the distance x in the direction of the force. In order to do such work, acceleration a = F/m is required according to Newton’s second law of motion.
So the Feynman drag argument is today disproved by the Casimir effect and other experiments of quantum field theory, a theory which he formulated!
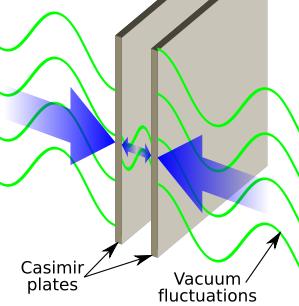 Above: the Casimir effect is that two nearby metal places are electrically conductive so only short wavelengths of virtual photons from the vacuum’s quantum field can exist by fitting into the small gap between them, but all wavelengths of virtual particles can push the plates together from outside! So the places appear to ‘attract’ one another, by mechanism of the the vacuum virtual photons pushing them together! The Casimir force is precisely predicted by quantum field theory and has been experimentally observed in accurate observations. [Illustration credit: Wikipedia.]
Above: the Casimir effect is that two nearby metal places are electrically conductive so only short wavelengths of virtual photons from the vacuum’s quantum field can exist by fitting into the small gap between them, but all wavelengths of virtual particles can push the plates together from outside! So the places appear to ‘attract’ one another, by mechanism of the the vacuum virtual photons pushing them together! The Casimir force is precisely predicted by quantum field theory and has been experimentally observed in accurate observations. [Illustration credit: Wikipedia.]
Virtual radiations which cause forces, simply don’t behave like ‘real’ particles. They don’t cause heating (which was an objection Poincare had to LeSage, claiming that the exchange of particles to cause gravity or any stronger force would make masses red hot!) because of the mechanism explained in my post Electricity and Quantum field theory:
1. When electric energy enters a vacuum-dielectric capacitor (or vacuum insulator open ended transmission line, which behaves like the capacitor!), it does so as electromagnetic field energy, at light velocity. Around each conductor there is charged (positive or negative) gauge boson field energy propagating forward at the velocity of light for the surrounding insulator (the vacuum in this case).
2. When the electromagnetic energy reaches the end of the capacitor plate or the end of the transmission line, it reflects back, still travelling at the velocity of light! It never slows or stops! Any ‘charged’ capacitor contains light-velocity energy trapped in it. The Heaviside ‘energy current’ or TEM wave (transverse electromagnetic wave) which is then travelling in each direction with equal energy (once a capacitor has been charged up and is in a ‘steady state’) causes no drag to electrons and therefore no electrical resistance (heating) whatsoever because there is no net drift of electrons along the wires or plates: such a drift requires a net variation of the field along the conductor, but that doesn’t happen because the flows of energy in opposite directions are equal. Electrons (and thus electric currents) only flow when there is an asymmetry in the gauge boson exchange rates in different directions.
Exchange radiations are normally in equilibrium. If an electron accelerates, it suffers a drag due to radiation resistance (i.e. it emits radiation in a direction perpendicular to the acceleration direction), while it is contracted in length by the Lorentz-FitzGerald contraction, so its geometry is automatically distorted by acceleration, which restores the equilibrium of gauge boson exchange. Once this occurs (during acceleration), equilibrium of gauge boson exchange to different directions is restored, so no further drag occurs.

Above: the flattening of a charge in the direction of its motion reduces drag (instead of increasing it!) because the relative number of field lines is reduced in the direction of motion but is unaffected in other directions, such as the transverse direction. This compensates for the motion of the particle by reducing drag from the field quanta. A net force only acts during acceleration when the shape is changing, this force is the inertia! A particle moving at the velocity of light such as a photon is a 1-dimensional pencil in the direction of motion, which makes its field lines 100% transverse since they stick out at right angles. This makes the photon a ‘disc’ shape when you look at the field lines. The more lines per unit volume pointing in one direction, the stronger the field in that direction. There is endless confusion about the ‘shape’ of particles in electromagnetism!
See the recent article by Carlos Barceló and Gil Jannes, ‘A Real Lorentz-FitzGerald Contraction’, published in the peer-reviewed journal Foundations of Physics, Volume 38, Number 2, February 2008, pp. 191-199:
‘Many condensed matter systems are such that their collective excitations at low energies can be described by fields satisfying equations of motion formally indistinguishable from those of relativistic field theory. The finite speed of propagation of the disturbances in the effective fields (in the simplest models, the speed of sound) plays here the role of the speed of light in fundamental physics. However, these apparently relativistic fields are immersed in an external Newtonian world (the condensed matter system itself and the laboratory can be considered Newtonian, since all the velocities involved are much smaller than the velocity of light) which provides a privileged coordinate system and therefore seems to destroy the possibility of having a perfectly defined relativistic emergent world. In this essay we ask ourselves the following question: In a homogeneous condensed matter medium, is there a way for internal observers, dealing exclusively with the low-energy collective phenomena, to detect their state of uniform motion with respect to the medium? By proposing a thought experiment based on the construction of a Michelson-Morley interferometer made of quasi-particles, we show that a real Lorentz-FitzGerald contraction takes place, so that internal observers are unable to find out anything about their ‘absolute’ state of motion. Therefore, we also show that an effective but perfectly defined relativistic world can emerge in a fishbowl world situated inside a Newtonian (laboratory) system. This leads us to reflect on the various levels of description in physics, in particular regarding the quest towards a theory of quantum gravity.’
Full text: http://arxiv.org/PS_cache/arxiv/pdf/0705/0705.4652v2.pdf, where page 4 states:
‘The reason that special relativity was considered a better explanation than the Lorentz-FitzGerald hypothesis can best be illustrated by Einstein’s own words: “The introduction of a ‘luminiferous ether’ will prove to be superfluous inasmuch as the view here to be developed will not require an ‘absolutely stationary space’ provided with special properties.” The ether theory had not been disproved, it merely became superfluous. Einstein realised that the knowledge of the elementary interactions of matter was not advanced enough to make any claim about the relation between the constitution of matter (the ‘molecular forces’), and a deeper layer of description (the ‘ether’) with certainty. Thus his formulation of special relativity was an advance within the given context, precisely because it avoided making any claim about the fundamental structure of matter, and limited itself to an effective macroscopic description.’
Now back to Feynman’s book ‘The Character of Physical Law’, Penguin, 1992, page 97: during his November 1964 lecture Symmetry in Physical Law, Feynman debunks the religion of ‘special’ relativity:
‘We cannot say that all motion is relative. That is not the content of relativity. Relativity says that uniform velocity in a straight line relative to the nebulae is undetectable.’
On pages 7-9 and 7-10 of volume 1 of The Feynman Lectures on Physics, Feynman states: ‘What is gravity? … What about the machinery of it? … Newton made no hypotheses about this; he was satisfied to find what it did without getting into the machinery of it. No one has since given any machinery. It is characteristic of the physical laws to have this abstract character. … Why can we use mathematics to describe nature without a mechanism behind it? No one knows. We have to keep going because we find out more that way.
‘Many mechanisms of gravitation have been suggested [‘It has been said that more than 200 theories of gravitation have been put forward; but the most plausible of these have all had the defect that they lead nowhere and admit of no experimental test.’ – Sir Arthur Eddington, Space Time and Gravitation, Cambridge University Press, 1921, p64; nowadays 10 dimensional supergravity adds a landscape of another 10500 spin-2 gravity theories to the 200 of Eddington’s time, all of which are wrong or not even wrong]. It is interesting to consider one of these, which many people have thought of from time to time. At first, one is quite excited and happy when he “discovers” it, but he soon finds that it is not correct. It was first discovered about 1750. Suppose there were many particles moving in space at a very high speed in all directions and being only slightly absorbed in going through matter. When they are absorbed, they give an impulse to the earth. However, since there are as many going one way as another, the impulses all balance. But when the sun is nearby, the particles coming toward the earth through the sun are partially absorbed, so fewer of them are coming from the sun than are coming from the other side. Therefore, the earth feels a net impulse toward the sun and it does not take one long to see that it is inversely as the square of the distance – because of the variation of the solid angle that the sun subtends as we vary the distance. What is wrong with that machinery? … the earth would feel a resistance to motion [Duh! Lorentz-FitzGerald contraction and inertia are both resistance effects in the vacuum! Also, the Casimir effect known since 1948 demonstrates that the vacuum is full of virtual radiation, which doesn not slow down the planets!] and would be stopping up in its orbit [and becoming red hot with the heat from the energy delivered by all the impacts of gauge bosons, as Poincare argued in stupidly dismissing quantum fields].’
Feynman further on that same page (p. 7-10, vol. 1) discusses the unification of electricity and gravitation:
‘Next we shall discuss the possible relation of gravitation to other forces. There is no explanation of gravitation in terms of other forces at the present time. … However … the force of electricity between two charged objects looks just like the law of gravitation … Perhaps gravitation and electricity are much more closely related than we think. Many attempts have been made to unify them; the so-called unified field theory is only a very elegant attempt to combine electricity and gravitation; but in comparing gravitation and electricity, the most interesting thing is the relative strength of the forces. Any theory that contains them both must also deduce how strong gravity is. … it has been proposed that the gravitational constant is related to the age of the universe. If that were the case, the gravitational constant would change with time … It turns out that if we consider the structure of the sun – the balance between the weight of its material and the rate at which radiant energy is generated inside it – we can deduce that if gravity were 10 percent stronger [1,000 million years ago], the sun would be much more than 10 percent brighter – by the sixth power of the gravity constant! … the earth would be about 100 degrees centigrade hotter, and all of the water would not have been in the sea, but vapor in the air, so life would not have started in the sea. So we do not now believe that the gravity constant is changing …’
This is wrong because Feynman is firstly following Teller’s stupidity in believing that despite the connection between electricity and gravitation, only the gravitational constant is varying, and secondly he assumes if it varied it was bigger instead of smaller in the past! If gravitation and electromagnetism are unified, both forces vary, so that the sun’s brightness will be independent of either constant. This is because fusion rates are increased on the compression caused by gravity on the mass of the star, but fusion rates are decreased by the electromagnetic repulsion between protons, which offsets the effect of gravity! So the enhanced fusion effect of a variation of the gravity ‘constant’ with time will be masked by the corresponding reduced fusion effect of the variation in the electromagnetic force constant! The same applies to the big bang fusion processes, where again gravitational constant compression variations will be masked by corresponding Coulomb repulsion variations.
I pointed this out to Professor Sean Carroll (who simply ignored me), who in a blog comment stated he knew a student writing papers claiming to disprove varying G by showing that fusion rates in the big bang depend on G! This is complete nonsense, because any variation of G will be accompanied by a variation of Coulomb force between protons which will mask the effect on fusion rates. The fact is that G increases with time instead of falling; this has no major effect on fusion rates in the big bang or in stars because the accompanying increase in Coulomb force repulsion offsets the effect of increasing gravitational compression. One important effect of the time variation of G is in the seeding of galaxies by density fluctuations in the early universe. The tiny ripples in the cosmic background radiation were enough to seed galaxies because G has been increasing all the time; this replaces the need for Guth’s ‘inflationary universe’. Guth’s inflationary theory assumes constant G and hence falsely requires faster-than-light expansion within a fraction of a second of the early universe in order to explain why the ripples in the cosmic background radiation were so smooth all over the sky at 300,000 years when the cosmic background radiation was emitted (just before the universe became de-ionized and transparent as electrons combined with ions).
Instead of ‘inflationary’ faster-than-light expansion explaining why the density fluctuations across the universe were so small at 300,000 years after the big bang, the correct explanation is that G was far smaller than currently believed at that time, because G is in fact directly proportional to the age of the universe.
Fig. 1 – quantum gravity. Note that general relativity with an ad hoc small positive cosmological constant, lambda (the so-called ‘lambda-Cold Dark Matter’ or ‘lambda-CDM’ model of cosmology) is useful in some ways but is a classical theory which is fitted to observations using ad hoc adjustments for dark energy and dark matter, which it doesn’t predict. General relativity is a step forward from Newtonian physics because it includes relativistic phenomenon and also the conservation of energy in gravitational fields which Newtonian gravitation ignores; but it is still an unquantized classical approximation which can be fitted to a whole ‘landscape’ of different universe models, so it’s predictive power in cosmology is limited: see the paper by Richard Lieu of the Physics Department, University of Alabama, ‘Lambda-CDM cosmology: how much suppression of credible evidence, and does the model really lead its competitors, using all evidence?’, http://arxiv.org/abs/0705.2462.
For more on the relationship of general relativity to quantum gravity, see the previous blog posts https://nige.wordpress.com/2007/07/04/metrics-and-gravitation/ (which contains a discussion of the mathematics of general relativity), https://nige.wordpress.com/2007/06/13/feynman-diagrams-in-loop-quantum-gravity-path-integrals-and-the-relationship-of-leptons-to-quarks (its Fig. 1 shows the difference between a Feynman diagram for general relativity and one for quantum gravity), and https://nige.wordpress.com/2006/09/30/keplers-law-from-kinetic-energy together with https://nige.wordpress.com/2006/09/22/gravity-equation-discredits-lubos-motl together have some relevance. Four other earlier posts which also contain some relevant material are https://nige.wordpress.com/2007/06/20/the-mathematical-errors-in-the-standard-model-of-particle-physics, https://nige.wordpress.com/2007/06/20/path-integrals-for-gauge-boson-radiation-versus-path-integrals-for-real-particles-and-weyls-gauge-symmetry-principle, https://nige.wordpress.com/path-integrals (which is under revision and will be improved), and https://nige.wordpress.com/2007/02/20/the-physics-of-quantum-field-theory (which is also being revised).
In Fig. 1 above, the observer (or test particle of mass) is in the centre of a frame of reference with isotropically receding matter at distance R. Beneath the observer at distance r there is a fundamental particle with mass, which introduces an asymmetry by interacting with some of the gravitons that the observer exchanges with the surrounding universe.
The result is gravity: gravitons accelerate the observer towards the fundamental particle of mass, as air pressure pushes a suction cup against a smooth surface. As proved (see Fig. 2 below with the proof following it), there is a cosmological acceleration of matter a = Hc where H is Hubble’s parameter. We observe an isotropic expansion of the universe about us, so receding masses M give rise to a radial outward force by Newton’s 2nd law F = Ma = MHc.
Newton’s 3rd law tells us that this action has an equal and opposite reaction, which from the possibilities known suggests the source of the gravitational field: the quantum gravity exchange radiation (that is exchanged between fundamental particles with mass/energy to cause gravitational interactions), i.e., gravitons, carry an inward force from distant receding matter. Where this is shielded (small amounts of nearby matter have little outward force, so they don’t exchange gravitons as forcefully as the immense distant receding masses, i.e. nearby mass automatically acts as a shield to forceful graviton exchange with the masses in the universe beyond the shield) the observer is pushed down towards the particle which acts as a shield.
Time past T in Hubble’s galaxy cluster recession law v = HR = HcT is related to the time t since the big bang by the relation
t + T = 1/H
(see Figure 1, above)
=> v = HcT = Hc[(1/H) – t] = c – (Hct)
=> a = dv/dt = d[c – (Hct)]/dt = –Hc,
the outward acceleration discovered observationally in 1998 (it was predicted in 1996). Force, F=ma. Newton’s 3rd law gives reaction force, inward directed gravitons. Since non-receding nearby masses don’t cause such a reaction force, the non-receding nearby mass below the central observer (in Fig. 1 above) shields that observer from graviton exchange with more distant masses in that direction; an asymmetry which produces gravity.
The spin-2 mainstream graviton idea is not even wrong because it falsely assumes that two masses are attracted by graviton exchange, and gives no mechanism to prevent the stronger exchange of gravitons between those masses and all the other masses in the entire universe (the proofs of spin-2 graviton theories fatally ignore graviton exchanges with all other masses in the universe, by implicitly assuming falsely that the universe is completely empty apart from the two attracting masses being considered; correcting this error changes everything!). This model is fact-based unlike extradimensional string theory, and makes falsifiable quantitative predictions!
The cross-sectional area of a fundamental particles of matter for quantum gravity interactions is found (independently of the fact-based assumptions behind this particular calculation) to be the black hole event horizon cross sectional area for the mass of the fundamental particle, π(2GM/c2)2. The net force (downward) in Fig. 1 is the simple product:
F = {total-inward directed graviton force, i.e. F = MHc}.{fraction of total force which is uncancelled, due to the asymmetry caused by mass m below the observer}
= MHc.{fraction of total force which is uncancelled, due to the asymmetry caused by mass m below the observer}
=MHc.{[π(2GM/c2)2].[(R/r)2]/[4πR2]}
Introducing M = (4/3)πR3r (using constant density, r, is just an approximation here to get you to see the key concept to the basic physics; see previous posts for corrections for the variation in effective density r with observable spacetime distance R) gives us three things immediately: (1) the inverse square law of general relativity for weak fields, (2) a checkable quantitative prediction for the strength of gravitation G, and also (3) a basis for quantizing mass in quantum field theory, since the force is proportional to the square of m, showing that m is the building block of all particle masses.
Copy of comment to http://kea-monad.blogspot.com/2008/12/standing-still.html
If I can be a bit unpopular, there is a reality to “dark energy”. The error is in the original fitting of general relativity to Hubble’s recession law. There are two times, time since the big bang t and time past T, which are related to one another by the formula t + T = 1/H (for proof of this relationship, simply see Fig. 1 here) in a flat spacetime cosmology (H being Hubble’s parameter). Hubble’s empirical law v = HR can – if Minkowski’s concept of spacetime R = ct is true – then be written as v = HR = H(ct) = Hc[(1/H) – T] = c(1 – HT). If we differentiate the expansion rate v as a function of time since the big bang T, we get acceleration, a = dv/dt = d[c(1 – HT)]/dT = -Hc = 6*10^(-10) ms^(-2), which is the observed tiny acceleration of the universe (so small that it is only detectable over immense amounts of spacetime, hence the reason why it was only discovered in 1997 by Perlmutter et al., for extremely redshifted supernovae at half the age of the universe). This was predicted and published well before Perlmutter, but that isn’t the point. The main point is that it is still ignored.
“Dark energy” isn’t so wrong, as the use of spacetime in general relativity as applied to cosmology. By choosing to interpret the Hubble recession as v = HR instead of (Minkowski’s equivalent of) v = Hct, the effective variation of velocity as a function of time (acceleration = dv/dt) is obscured from sight, and valuable physical insight is lost from mainstream cosmology. When the facts are pointed out, instead of cosmologists grasping the significance of this, they try to ignore it.
The significance is that the acceleration of the flat universe is inherent in the way the universe is expanding according to Hubble’s 1929 discovery. In other words, the expansion and the acceleration are not two separate things, but different aspects of the same thing: the dark energy isn’t just causing the acceleration of the universe, it’s causing the very expansion of the universe, too. So now there is general repulsive force, powered by dark energy, causing the expansion of the universe.
Now we have to introduce gravitons. Fietz and Pauli in the 1930s originally ignored all the mass-energy in the universe except for two small test particles when analyzing quantum gravity. If a quantum exchange between two masses (similar gravitational charges) results in attraction and there is no other process going on, then the graviton would have to have spin-2.
However, clearly there is a lot more going on, because there is no mechanism to stop gravitons being exchange not merely between two test masses, but between each of those masses and all the other masses in the universe.
Normally we can ignore the other masses in the universe when thinking of gravity, but not with graviton exchange. The problem with ignoring the rest of the mass of the universe is that it is nearly 100% of the total mass partaking in the interaction between your test masses, so [you] would be ignoring nearly all of mass involved. Although classically you can often ignore the rest of the distant mass of the universe because it is quite uniformly distributed across the sky, this doesn’t cancel out when you are considering quantum graviton exchanges. In any case, gravitons will be converging as they travel from the distant masses in the universe to any particular small test mass. This convergence of gravitons has geometric effects. The short story is that Pauli and Fietz’s approximation of ignoring 99.9999…% of the mass in the universe when “proving” that gravitons must be spin-2, is plain wrong. Once you involve the entire mass of the universe – because there is no mechanism known which can stop such graviton exchanges becoming involved in every single quantum gravitational interaction between a few small masses – you find that gravitons must have spin-1 and must produce observed gravitation by pushing masses together over distances up to something like the average supercluster separation distance.
Beyond that distance, the exchange causes the net repulsion that is responsible for the expansion and also the acceleration of the universe.
That “attraction” and repulsion can both be caused by the same spin-1 gravitons (which are dark energy) can be understood by a semi-valid analogy, the baking cake. As the cake expands, the particles in it recede as if there is a repulsion between them. But if there are some nearby raisins in the cake, they will be pressed even closer together by the this pressure, because they are more strongly bound against expansion than the dough, and because they are being pressed on all sides apart from the sides facing adjacent raisins. So because there is no significant amount of expanding dough between them, they shield one another and get pressed closer together by the expansion of the surrounding dough.
In quantum gravity, one simple way to analyze this mathematically is by the empirical laws of mechanics. The acceleration of the universe means that distant receding masses have an acceleration outward from the observer. If the mass of a particular receding object is m and its acceleration a, for non-relativistic recession velocities this mass possesses an effective outward force given by Newton’s 2nd law, F = ma. So a 1 kg mass receding at 6*10^(-10) ms^(-2) will have an outward force of 6*10^(-10) Newtons. This sounds trivial, but actually the mass of the receding universe is very large, so the total outward force is very large indeed. Newton’s 3rd law then tells you of an equal and opposite reaction force. This is the inward-directed graviton-mediated exchange force. So you can make quantitative predictions immediately.
The clever thing is that for two nearby masses which are not significantly receding from one another (say apple and Earth), this mechanics tells you immediately that there is no significant reaction force of gravitons from apple to Earth or vice-versa.
So by this effect there is a “shadowing” of gravitational charges by each other (because gravitons interact with gravitational charges in order to mediate the force of gravity, and don’t go straight through unaffected), providing that they are nearby enough that they are not receding significantly. Thus, the gravitons exchanged between the apple and the receding masses in the universe above it cause most of the observed gravitational effect: the apple is pushed downwards towards the earth by spin-1 gravitons.
So the mainstream QFT gets off beam by focussing on (1) spin-2 graviton errors without correcting them, (2) Hubble v = HR obfuscation in place of the more physically helpful spacetime equivalent of v = Hct, and (3) high energy quantum graviton interactions such as Planck scale unification, instead of focussing on building a empirically-defensible, checkable, testable, falsifiable model of quantum gravity which is successful at the low-energy scale and which resolves problems in general relativity by predicting things such as
(1) G,
(2) the amount of dark energy/cosmological acceleration, and
(3) the flatness of the universe without the speculative inflation hypothesis.
I.e., it’s a non-speculative theory, a fact-based theory which at each step is defensible, and which produces predictions that can be checked.
The reason for the ignorance of the simplicity of QFT at low energy is due to the fact that mainstream QFT is contradictory in:
(1) accepting Schwinger’s renormalization work, in which the vacuum is only chaotic (with spacetime loops of pair-production virtual fermions continually annihilating into virtual bosons, and back again) in electric fields above ~10^18 volts/metre, which occurs only out to a short distance (a matter of femtometres) from fundamental particles like quarks and electrons. These virtual spacetime creation-annihilation “loops” therefore don’t fill the entirity of spacetime, just a small volume around particles of real matter. Hence, the vacuum as a whole isn’t filled with chaotic annihilation-creation loops. If it was, the IR cutoff energy for the QED running coupling would be zero, which it isn’t. There has to be a limiting range to distance out to which there is any virtual pair production in the vacuum around a real fermion, otherwise the virtual fermions would be able to polarize sufficiently to totally cancel out the electric charge of real fermions. Penrose makes this clear with a diagram in “Road to Reality”. The virtual fermions polarize radially around a real fermion core, cancelling out much of the field and explaining why the “bare core” charge of a real fermion is higher in QFT than the observed charge of a fermion as observed in low energy physics. If there was no limit on this range of vacuum polarization due to pair production, you would end up with the electron having an electric charge of zero at low energy. This isn’t true, so as Schwinger argued, the vacuum is only polarized in strong electric fields (ref.: eq. 359 of http://arxiv.org/abs/quant-ph/0608140 or see eq. 8.20 of http://arxiv.org/abs/hep-th/0510040 – this is all entirely mainstream stuff, and is very well tested in QED calculations, and is not speculative guesswork).
(2) claiming that the entire vacuum is filled with chaotic creation-annihilation loops. This claim is made in most popular books by Hawking and many others. They don’t grasp that if the vacuum were filled with virtual fermions in such loops, you’d get not just geometric (inverse-square law) divergence of electric field lines from charges, but also a massive exponential attenuation factor which would cancel out those radial electric field lines within a tiny distance. Even if we take Penrose’s guess that the core electric charge of the electron is 11.7 times the value observed at low energy, then the polarized vacuum reduces the electric charge by this factor over a distance of merely femtometres. Hence, without the Schwinger cutoff on pair-production below ~10^18 v/m, you would get zero observable electric charge at distances beyond a nanometre from an electron. Clearly, therefore, the vacuum is not filled with polarizable virtual fermions, and isn’t therefore filled with annihilation-creation loops of virtual particles.
This argument is experimentally defensible, and so is extremely strong. The vacuum effects which cause chaos are limited to strong fields, very close to fermions. Beyond a matter of mere femtometres, the vacuum isn’t chaotic and is far simpler, with merely virtual (gauge) bosons which can’t undergo pair production until they enter the strong field near a fermion.
It’s simple to understand all this if you know about radiation. Lead, and other high atomic number elements, attenuates real gamma rays of high energy primarily by pair production. The gamma ray passes into the strong field near the nucleus, and is transformed into an electron and positron pair. This pair can then be polarized by an external electric field, attenuating or shielding that external electric field, before the pair annihilate back into a fresh gamma ray. The field shielding process with virtual photons and virtual fermions is similar in principle to that observed with real radiation and with the real dielectrics you put inside capacitors between the plates, so the dielectrics polarize to store large amounts of energy. (There is nothing mysterious or speculative in this basic physics.)
Away from the strong fields that exist very close to real fermions, the vacuum is very simple and just contains virtual bosons flying around. Because they don’t (unlike fermions) behave the exclusion principle, they don’t behave like a compressed gas. They mediate fundamental forces by being exchanged between fermions, simply, without loopy chaos.
Quantum gravity can be done the same way at low energy! It’s a simple geometric situation. Loops are important only at high energy where they occur due to pair-production as already proved, so it’s amazing how much ignorance, apathy and sheer insulting dumbness there is amongst some QFT theorists, obsessed with unobservable Planck scale phenomena and uncheckable imaginary spin-2 gravitons.
“Dark energy” is badly understood by the mainstream, and having a Lambda term in the field equation of GR is not sufficient physics. It’s ad hoc juggling. I just think that for the record, there is evidence that “dark energy” is real, it’s spin-1 gravitons and low energy quantum field theory physics is nothing like the unphysical mathematical obfuscation currently being masqueraded as QFT. Fields are due to physical phenomena, not equations that are approximate models. To understand QFT, what is needed is not just a Lie algebra textbook but understanding of physical processes like pair production (which is real and occurs when high energy gamma rays enter strong fields), polarization of such charges (again a physical fact, well known in electronics since it’s used in electrolytic capacitors), and spacetime.
The right way to deny all progress in the world is to be reasonable and quiet to fit in with status quo, in an attempt to win or keep friends. As Shaw wrote in 1903:
“The reasonable man adapts himself to the world; the unreasonable one persists in trying to adapt the world to himself. Therefore all progress depends on the unreasonable man.”
I think Louise is right in her basic equation, and also in dismissing the terrible ad hoc mainstream approach to “dark energy”, but that doesn’t mean that fundamentally there is [no] dark energy in the form of gravitons flying around, allowing predictions to be checked.
Please delete if this comment is unhelpful to the status quo here. (I’ll copy it to my blog as proof of my unreasonableness. Maybe it’s just too long, but it does take space to explain anything in sufficient detail to get the main points across.)
- **************************
Notes on Lunsford’s comment to the blog post:
http://dorigo.wordpress.com/2009/01/08/black-holes-the-winged-seeds/
Lunsford refers to Cooperstock and Tieu, General Relativity Resolves Galactic Rotation Without Exotic Dark Matter, http://arxiv.org/abs/astro-ph/0507619, pp. 17-18:
‘One might be inclined to question how this large departure from the Newtonian picture regarding galactic rotation curves could have arisen since the planetary motion problem is also a gravitationally bound system and the deviations there using general relativity are so small. The reason is that the two problems are very different: in the planetary problem, the source of gravity is the sun and the planets are treated as test particles in this field (apart from contributing minor perturbations when necessary). They respond to the field of the sun but they do not contribute to the field. By contrast, in the galaxy problem, the source of the field is the combined rotating mass of all of the freely-gravitating elements themselves that compose the galaxy.’
Sean Carroll criticised it on a technical level because he felt it wasn’t rigorous: http://blogs.discovermagazine.com/cosmicvariance/2005/10/17/escape-from-the-clutches-of-the-dark-sector/
But I’ve seen a different, cleaner or more straightforward-looking analysis of the galactic rotation curves by Hunter that appears to tackle the dark matter problem at http://www.gravity.uk.com/galactic_rotation_curves.html (I want to point out though that I don’t agree or recommend the cosmology pages on the rest of that site). His interesting starting point is the equivalence of rest mass energy to gravitational potential energy of the mass with respect to the surrounding universe. If the universe collapsed under gravity, such potential energy would be released. It’s thus a nice conjecture (equivalent to Louise’s equation since cancelling m and inserting r = ct into E = mc^2 = mMG/r gives c^2 = MG/(ct), or Louise’s tc^3 = MG), and leads to flat galactic rotation curves without the intervention of enormous quantities of unobserved matter within galaxies (there is obviously some dark matter, from other observations like neutrino masses, etc.).
But this is pretty trivial compared to the issue of quantum gravity. What should be up for discussion is Lunsford’s paper http://cdsweb.cern.ch/record/688763?ln=en but it is just too abstract for most people. Even people who have done QM and cosmology courses (including basic GR) don’t have the mathematical physics background to understand the use of GR and QFT in that paper, e.g. the differential geometry, variational principle, and so on.
I wish he could write a basic textbook of the mathematical foundations used in his paper. I’ve learned some useful mathematics from McMahon’s Quantum Field Theory Demystified (2008), Zee’s Quantum Field Theory in a Nutshell (2003) Dyson’s http://arxiv.org/PS_cache/quant-ph/pdf/0608/0608140v1.pdf and the QFT lectures http://arxiv.org/PS_cache/hep-th/pdf/0510/0510040v2.pdf
A QFT of gravity will differ from GR. Instead of curved spacetime, you have discrete graviton exchanges causing the interactions (gravity, inertia, and the contraction of both stationary and moving bodies composed of mass-energy). Some energy will exist in the graviton field, and surely this is the dark energy. There is no supplemental ‘cosmological constant’ of dark energy in addition to the gravitational field. Instead, the gravitational field of graviton exchanges between masses will cause expansion on large distances and attraction on smaller ones.
Think of the analogy of a raisin cake expanding due to the motion of the dough. Nearby raisins (with little or no dough between them) will be pushed closer together like ‘attraction’, while distant raisins will be accelerated further apart during the cooking, like a ‘repulsion’ effect. Two phenomena for the price of one graviton field! No additional dark energy or CC, just the plain old gravitational field. I think this is missed by the mainstream because they (1) think LeSage came up with quantum gravity and was disproved (he didn’t, and the objections to his ideas came because he didn’t have gravitons exchange radiation, but a gas), and (2) the Pauli-Fierz ‘proof’ that gravitons exchanged between 2 masses to cause them to attract, must suck, which implies spin-2 suckers.
Actually the Pauli-Fierz proof is fine if the universe only contains 2 masses which ‘attract’. Problem is, it doesn’t contain 2 masses. We’re surrounded by masses, and there is no mechanism to stop graviton exchanges with those masses. As gravitons propagate from distant masses to nearby ones, they converge (not diverge), so the effects of the distant masses are larger (not smaller) that that of nearby masses. Once you include these masses, the whole basis of the Pauli-Fietz proof evaporates; gravitons no longer need to be suckers and thus don’t need to have a spin of 2. Instead of having spin-2 gravitons sucking 2 masses together in an otherwise empty universe, you really have those masses being pushed together by graviton exchanges with the immense masses in the surrounding universe. This is so totally obvious, it’s amazing why the mainstream is so obsessed with spin-2 suckers. (Probably because string theory is the framework for spin-2 suckers.)
Update (18 February 2009):
Dr Woit’s Not Even Wrong weblog has a nice discussion about the current status of the string theory propaganda war:
http://www.math.columbia.edu/~woit/wordpress/?p=1630
Mission Accomplished
A few years ago the asset value of string theory in the market-place of ideas started to take a tumble due to the increasingly obvious failure of the idea of unifying physics with a 10/11 dimensional string/M-theory. Since then a few string theorists and their supporters have decided to fight back with an effort to regain market-share by misleading the public about what has happened. Because the nature of this failure is sometimes summarized as “string theory makes no experimental predictions”, the tactic often used is to claim that “string theory DOES make predictions”, while neglecting to explain that this claim has nothing to do with string theory unification.
A favorite way to do this is to invoke recent attempts to use conjectural string/gauge dualities to provide an approximate calculational method for some strongly coupled quantum systems. There are active on-going research programs to try and see if such calculational methods are useful in the case of heavy-ion collisions and various condensed-matter systems. In the heavy-ion case, we believe we know the underlying theory (QCD), so any contact between such calculations and experiment is a test not of the theory, but of the calculational method. For the condensed matter systems, what is being tested is the combination of the strongly-coupled model and the calculational method. None of this has anything to do with testing the idea that string theory provides a fundamental unified theory. …
The one string theorist involved in all this was Clifford Johnson, who gives a minute-by-minute description of his participation here. It ends by invoking the phrase made famous by the last US president:
“Mission accomplished. (Hurrah!)”
http://www.math.columbia.edu/~woit/wordpress/?p=1630&cpage=1#comment-46927
Acknowledging that this work does not prove string theory unification isn’t the point. Instead of just stating that the research under discussion has nothing to do with the string theory unification, Clifford is claiming that it does (using the logic: “we don’t understand string theory, maybe comparing AdS/CFT-motivated approximations to experimental results in heavy-ion physics will help us understand string theory, and once we understand string theory, we’ll see how to do string theory unification”). He’s welcome to that bit of wishful thinking, but when he uses it on non-experts in the way quoted, it’s not at all surprising that what they take away is the message that string theory unification is moving forward due to this first connection between string theory and experiment. …
There follows an anonymous attack on Dr Woit:
‘As I have said repeatedly, you adamantly refuse to recognize the UNDERSTANDING we have gleamed through string theory, while knocking it for the lack of experiments.’ – Somebody [anonymous attack on Dr Woit]
I thought the kind of physics string theorists were claiming to do was of the “Shut up and calculate!” variety. But now suddenly we have a benefit from string theory that you get an extradimensional “understanding” of physics because of the (unproved) conjecture that 5-dimensional AdS space (which is not cosmological space, because it has a negative CC instead of positive) may be helpful in modelling strong interactions.
Duh! Yes, maybe it’s helpful in a new approximation for QCD calculations, but that’s not understanding physical reality because AdS isn’t real spacetime. It’s just a calculational tool. Similarly, classical physics like GR is just a calculational tool; it doesn’t help you to understand (quantum) nature, just to do approximate calculations.
Because orbits of planets are elliptical with the sun at one focus, the planets speed up when near the sun, and this causes effects like time dilation and it also causes their mass to increase due to relativistic effects (this is significant for Mercury, which is closest to the sun and orbits fastest). Although this effect is insignificant over a single orbit, so it didn’t affect the observations of Brahe or Kepler’s laws upon which Newton’s inverse square law was based, the effect accumulates and is substantial over a period of centuries, because it the perhelion of the orbit precesses. Only part of the precession is due to relativistic effects, but it is still an important anomaly in the Newtonian scheme. Einstein and Hilbert developed general relativity to deal with such problems. Significantly, the failure of Newtonian gravity is most important for light, which is deflected by gravity twice as much when passing the sun as that predicted by Newton’s a = MG/r2.
Einstein recognised that gravitational acceleration and all other accelerations are represented by a curved worldline on a plot of distance travelled versus time. This is the curvature of spacetime; you see it as the curved line when you plot the height of a falling apple versus time.
Einstein then used tensor calculus to represent such curvatures by the Ricci curvature tensor, Rab, and he tried to equate this with the source of the accelerative field, the tensor Tab, which represents all the causes of accelerations such as mass, energy, momentum and pressure. In order to represent Newton’s gravity law a = MG/r2 with such tensor calculus, Einstein began with the assumption of a direct relationship such as Rab = Tab. This simply says that mass-energy tells is directly proportional to curvature of spacetime. However, it is false since it violates the conservation of mass-energy. To make it consistent with the experimentally confirmed conservation of mass-energy, Einstein and Hilbert in November 1915 realised that you need to subtract from Tab on the right hand side the product of half the metric tensor, gab, and the trace, T (the sum of scalar terms, across the diagonal of the matrix for Tab). Hence
Rab = Tab – (1/2)gabT.
[This is usually re-written in the equivalent form, Rab – (1/2)gabR = Tab.]
There is a very simple way to demonstrate some of the applications and features of general relativity. Simply ignore 15 of the 16 terms in the matrix for Tab, and concentrate on the energy density component, T00, which is a scalar (it is the first term in the diagonal for the matrix) so it is exactly equal to its own trace:
T00 = T.
Hence, Rab = Tab – (1/2)gabT becomes
Rab = T00 – (1/2)gabT, and since T00 = T, we obtain
Rab = T[1 – (1/2)gab]
The metric tensor gab = ds2/(dxadxb), and it depends on the relativistic Lorentzian metric gamma factor, (1 – v2/c2)-1/2, so in general gab falls from about 1 towards 0 as velocity increases from v = 0 to v = c.
Hence, for low speeds where, approximately, v = 0 (i.e., v << c), gab is generally close to 1 so we have a curvature of
Rab = T[1 – (1/2)(1)] = T/2.
For high speeds where, approximately, v = c, we have gab = 0 so
Rab = T[1 – (1/2)(0)] = T.
The curvature experienced for an identical gravity source if you are moving at the velocity of light is therefore twice the amount of curvature you get at low (non-relativistic) velocities. This is the explanation as to why a photon moving at speed c gets twice as much curvature from the sun’s gravity (i.e., it gets deflected twice as much) as Newton’s law predicts for low speeds. It is important to note that general relativity doesn’t supply the physical mechanism for this effect. It works quantitatively because is its a mathematical package which accounts accurately for the use of energy.
However, it is clear from the way that general relativity works that the source of gravity doesn’t change when such velocity-dependent effects occur. A rapidly moving object falls faster than a slowly moving one because of the difference produced in way the moving object is subject to the gravitational field, i.e., the extra deflection of light is dependent upon the Lorentz-FitzGerald contraction (the gamma factor already mentioned), which alters length (for a object moving at speed c there are no electromagnetic field lines extending along the direction of propagation whatsoever, only at right angles to the direction of propagation, i.e., transversely). This increases the amount of interaction between the electromagnetic fields of photon and the gravitational field. Clearly, in a slow moving object, half of the electromagnetic field lines (which normally point randomly in all directions from matter, apart from minor asymmetries due to magnets, etc.), will be pointing in the wrong direction to interact with gravity, and so slow moving objects only experience half the curvature that fast moving ones do, in a similar gravitational field.
Some issues with general relativity are focussed on the assumed accuracy of Newtonian gravity which is put into the theory as the low speed, weak field solution normalization. E.g., as explained above in this post, gravitons cause both long-range cosmological repulsion (between substantially redshifted masses) and “attraction” between masses which aren’t strongly redshifted (rapidly receding) from one another, just as gas pressure has both “repulsive” (push) effects and apparent “attraction” effects: a sink plunger or rubber “suction” cup is “attracted” to a surface by air pressure pushing on it, while the pressure of gas in an exploding bomb accelerates bits of matter outward in all directions like a “repulsive” force. None of this is very hi-tech.
Here’s a funny claim by the mathematician Gill Kalai defending the spin-2 stringy crackpot theory of gravity which has a landscape of 10500 vacua and can’t predict anything checkable:
http://www.math.columbia.edu/~woit/wordpress/?p=1630&cpage=1#comment-46932
‘Successful applications of ST calculations in other areas can be regarded as a (weak) support for the theory itself.’ – Gil Kalai
Applying the Gill Kalai argument, the major direct successes of classical physics can be regarded as major support for classical theory over quantum theory! Yeah, right!
Update:
Gill has queried my criticism above in the comments section (below), and I have replied there as follows:
You argue that successful applications of a theory (ST) to other areas than the key areas provides weak support for the original theory!
Applying your argument to classical physics, the much stronger successes of Maxwell’s equations of classical electromagnetism (for instance to thousands of situations in electromagnetism) will make that theory win hands-down over the relatively few things that you can specifically calculate using quantum electrodynamics (magnetic moments of leptons, Lamb shift in hydrogen spectra).
Your argument that you can have support for a theory from indirect successes ignores alternative ideas which do a lot better! E.g., there are alternatives to string theory which do make calculations that are checkable. Your argument specifically gives support to a failed theory of gravity because you are:
(1) not demanding that the failed theory of gravity (ST) require falsifiable predictions
and
(2) ignoring alternative ideas to string. Once you include alternative ideas, ST “successes” are shown to be failures by comparison.
What you are neglecting is that indirect calculational successes are no support for a theory: Ptolemy’s epicycles could enable predictions of apparent planetary motions, but that is not evidence. Model building by the AdS/CFT conjecture is not a falsifiable physics, any more than building theories of epicycles. You need falsifiable predictions of the key elements to the theory, to provide scientific evidence that supports the theory. To hype or defend a theory without even a single falsifiable prediction is appalling:
‘String theory has the remarkable property of predicting gravity.’ – Ed Witten, M-theory originator, Reflections on the Fate of Spacetime, Physics Today, April 1996.
This abuse of science is just the defence made for epicycles, phlogiston, caloric, etc. It just stagnates the entire field by leading to hype of drivel which creates so much noise that the more useful ideas can’t be heard.
Update:
Gil has responded in the comments below, saying that he doesn’t understand and that Ptolemy’s predictions via ad hoc epicycles were a major intellectual and scientific advance. My response:
Hi Gil,
Making predictions from a false mathematical model such as Ptolemy’s earth centred system, which is endlessly adjustable, or ST which relies on unobservables such as extra dimensions, may be useful until a better theory comes along, but it is not scientific! Such predictions are not falsifiable because the model is adjusted when it fails, for example by adding more epicycles to “correct” errors. With ST you can select different brane models, different parameters for the moduli of the Calabi-Yau manifold, etc.
In 250 BC, Aristarchus of Samos had the solar system theory. Ptolemy in 150 AD ridiculed Aristarchus’ solar system, falsely claiming that if it was true, with the earth spinning daily, clouds would be continuously shooting over the equator at 1000 miles/hour, and people would be thrown off by the motion. The problem with a false theory being defended for non-falsifiable applications is that it becomes dogma, leading to unwarranted attacks on more useful ideas.
I don’t agree that it was a giant intellectual and scientific achievement of the time. It was a step backwards from Aristarchus’ earlier solar system theory.
Going back to what you say you do not understand: you claimed that indirect applications of a theory provide weak support for the main theory. I point out that if indirect applications provide weak support as you claim, then direct applications of a theory such as classical theories will by analogy provide relatively strong support for the theory. Since you are ignoring other criteria (like the existence of alternative theories which do a better job) in judging whether ST is deemed to be supported by AdS/CFT and company, it follows from using your way of judging support for a theory, that since classical electromagnetism is relatively strong, classical electromagnetism would win out over QED which has fewer specifically unique predictions. Your argument that indirect applications lend some support to string theory is a big step backwards scientifically. Indirect applications don’t support a theory at all, successful falsifiable predictions of the main claims of the theory are needed to provide any support. Even then, the theory isn’t proved. Your statement on Not Even Wrong supports a retreat from Popper’s criterion of science back to the kind of low standards which accommodate fashionable nonsense, ad hoc modelling that doesn’t lead to progress in fundamental physics, but instead creates a belief system akin to religious groupthink, which becomes dogma and leads to correct alternative ideas being ignored or falsely dismissed.
Update:
I just have to quote a new attack on Dr Woit on the Not Even Wrong blog, which is so absurd and stuck-up it makes me laugh out loud!
http://www.math.columbia.edu/~woit/wordpress/?p=1630&cpage=1#comment-46967
‘This blog indeed has some scientific content, but in my opinion it does not qualify as genuine science research activity. You mentioned BRST, which is indeed a scientific topic, but presenting it in a blog, without peer review, without going through the usual channels of academic research, it remains the same category as science journalism and popular science writing. For example, if you would submit your work on BRST to a science journal where others would have the chance to seriously review it and it would get published, it would be a different story. But so far you did not do that. Even if you did, the publication on the blog, in my opinion, still doesn’t count as scientific research.
‘… this is not an attack on you, but the fact must be stated that you operate in an entirely different way than ordinary scientists who are doing active research.’ – Troy (anonymous attack on Dr Woit)
I’ve got to say that this is the most funny comment ever! It’s the most stuck-up example of officialdom in science, groupthink, etc., ever. Especially the ending: ‘you operate in an entirely different way than ordinary scientists’. What about the non-falsifiable speculations of string theorists? What about the culture of groupthink anti-science lies in the increasingly filthy mainstream peer-reviewed journals:
‘String theory has the remarkable property of predicting gravity’: false claim by Edward Witten in his grandiose piece Reflections on the Fate of Spacetime in the April 1996 issue of Physics Today,
and what about the use of such peer-reviewed mainstream lies to censor out the correct facts, as occurred when – to give just one little example – I submitted a paper for ‘peer-review’ to Classical and Quantum Gravity and the editor sent it to string theorists who sent back a report which the editor forwarded to me (without the names of the ‘peer-reviewers’) that ignored the physics and simply dismissed it for not being string theory work!
This argument that anybody who works far outside the fashionable mainstream, where normal peer-review breaks down (because of a lack of any genuine ‘peers’ capable of reviewing the work), can be dismissed as not a scientist because ‘you operate in an entirely different way than ordinary scientists’, in terms of publishing policy, is immensely funny! The way ‘ordinary scientists’ work on string ‘theory’ is a failure, and no amount of peer-review, hype, lying and mutual backslapping congratulations between members of the mainstream string camp will turn their non-falsifiable speculations into scientific facts. All those people have is mutual citation counts, an indicator of fashion not fact, and they really believe that popularity and fashion are scientific criteria! They believe that because they are failures judged by the real criteria of science, falsifiable scientific predictions and experimental checks of key ideas.
(It’s quite appropriate that the anonymous attacker used the name ‘Troy’, the city under siege which was so gullible that it let in the enemy soldiers, which had hidden inside a large wooden gift horse presented to Troy as a present. Believers of absurd claims for 10/11 dimensional string theory that cannot be tested are so gullible.)
Update:
Copy of a comment to Louise’s blog:
http://riofriospacetime.blogspot.com/2009/02/race-for-higgs-or-no-higgs.html
The interesting thing about the Higgs field is that it is linked to quantum gravity by being gravitational “charge”, i.e. mass. So sorting out the electroweak symmetry breaking mechanism in the Standard Model is a major step towards understanding the nature of mass and therefore the charge of quantum gravity. This is a point Dr Woit makes in his 2002 paper on electroweak symmetry, where he shows that you can potentially come up with symmetry groups that give the chiral symmetry features of the Standard Model using lie and clifford algebras. The Higgs field, like string theory, is something not observed yet prematurely celebrated and treated as orthodoxy. But it is not confirmed and is not part of the Standard Model symmetries, U(1) x SU(2) x SU(3). These symmetry groups describe the observed and known particles and symmetries of the universe, not the Higgs boson(s) and graviton. There is no evidence that U(1) x SU(2) is broken at low energy by Higgs. This symmetry is not there at low energy, but that doesn’t prove that the Higgs mechanism breaks it!
In addition to providing mass to SM particles, the role of the Higgs field is to break the electromagnetic interaction U(1) away from the whole U(1) x SU(2) x SU(3) symmetry, so that only U(1) exists at low energy because its gauge boson is massless (it doesn’t couple to the supposed Higgs field) unlike the other gauge bosons which acquire mass by coupling to the Higgs field boson(s).
The way a Higgs field is supposed to break electroweak symmetry is to give mass to all SU(2) weak gauge bosons at low energy, but leave them massless at high energy where you have symmetry.
This is just one specific way of breaking the U(1) x SU(2) symmetry, which has no experimental evidence to justify it, and it is not the simplest way. One simple way of doing adding gravitons and masses to the SM, as seen from my mechanistic gauge interaction perspective might be that, instead of having a Higgs field to give mass to all SU(2) gauge bosons at low energy but to none of them at at high [i.e. above electroweak unification] energy, we could have a chiral effect where one handedness of the SU(2) gauge bosons always has mass and the other is always massless.
The massless but electrically charged SU(2) gauge bosons then replace the usual U(1) electromagnetism, so you have positively charged massless bosons around protons giving rise to the positive electric field observed in the space there, and negatively charged massless bosons around electrons. (This model can casually explain the physics of electromagnetic attraction and repulsion, and makes falsifiable predictions about the strength of the electromagnetic interaction.) The massless, uncharged SU(2) gauge boson left over is the graviton, which explains why the gravitational coupling is 10^40 times weaker than electromagnetism in terms of the different way exchanged charged massless and uncharged massless gauge bosons interact with all the particles in the universe.
The one-handedness of SU(2) gauge bosons which does has mass, then gives rise the weak interaction as observed so far in experiments, explaining chiral symmetry because only one handedness of particles can experience weak interactions.
So my argument is that there the Higgs mechanism for mass is a wrong guess.
Symmetry is hidden in a different way. The gauge bosons of electromagnetism [and gravity] are the one massless handedness of SU(2) gauge bosons, the [massive handedness of SU(2) gauge bosons being the] particles that mediate short-range weak interactions. Although SU(2) x SU(3) expresses the symmetry of this theory, it is not a unified theory because SU(3) strong interactions shouldn’t have identical coupling strength to SU(2) at arbitrarily high energy: SU(2) couplings increase with energy due to seeing less vacuum polarization shielding, and this energy is at the expense of the SU(3) strong interaction which is physically powered by the energy used from SU(2) in producing polarized pair production loops of vacuum particles.
So my argument is that the symmetry of the universe is SU(2) x SU(3). Here, SU(3) is just as in the mainstream Standard Model, but SU(2) does a lot more than just weak interactions; massless versions of its 3 gauge bosons also provide electromagnetism (the 2 electrically charged massless gauge bosons) and gravity (the single electrically uncharged massless gauge boson is a spin-1 graviton).
Instead of the vacuum being filled with a Higgs field of massive bosons that mire charges, a discrete number of massive bosons interact via the electromagnetic interaction with each particle to give it mass; the origin of mass/gravitational charge as distinct from electromagnetic charge arises because the discrete number of massive bosons which interact with each fundamental particle (by analogy to a shell of electrons around a nucleus) each interact directly with gravitons. Electromagnetic charges (particle cores) do not interact directly with gravitons, only indirectly via interaction with massive bosons in the vacuum. This models all lepton and hadron masses if all the massive bosons in the vacuum have a mass equal to that of the Z_0 weak gauge boson, i.e. 91 GeV. I have to try to write up a paper on this.
My (now old) blog post which includes this topic is badly in need of being rewritten and condensed down a lot, to improve its clarity. I’m trying to follow the work of Carl and Kea with respect to neutrino mass matrices and extensions of the Koide formula to hadron masses, as well as working my way through Zee’s book, which tackles most of the questions in quantum field theory which motivate my interest (unlike several other QFT books, such as most of Weinberg).
At first glance, Ryder’s second edition QFT book seemed more accessible than Zee, but it turns out that the best explanation Ryder gives is the tensor form of Maxwell equations and how they relate to the vector calculus forms, which is neat. Zee gives path integral calculations for fundamental forces in gauge theory and for QED essentials such perturbative theory for calculating magnetic moments, which I find more motivating than the totally meaningless drivel that takes up vast amounts of math yet calculates nothing in several other QFT books (particularly those which end up declaring the beauty of string theory in the final part!).
Update: I should add that Ryder’s 2nd ed., pp. 298-306 (section 8.5, ‘The Weinberg-Salam Model’) is also very important and well written.
Update: the funniest blog comment I’ve read so far is Woit’s summary of a blog post by Motl, ‘He does draw some historical lessons, noting correctly that a theory developed for one purpose may turn out not to work for that, but find use elsewhere. For instance, a theory once thought to be a spaceship capable of giving a TOE may turn out to be a toaster capable of approximately describing the viscosity of a quark-gluon plasma….’
Update (25 March 2009): Dr Woit has another summary in his blog post called ‘The Nature of Truth’, which is also well worth quoting:
‘It is the fact that one needs to postulate a huge landscape in string theory in order to have something complicated and intractable enough to evade conflict with experiment that is the problem. … The failure … is … attributable to … the string theory-based assumption that fundamental physical theory involves a hopelessly complicated set of possibilities for low-energy physics.’
Emphasis added. It’s nice to document Dr Woit’s occasional hopeful argument that hopelessly complicated theories that predict nothing are headed in the wrong direction. However, this doesn’t mean that he supports the simplicity of the approach in this blog post. Maybe if I can disentangle the nascent excitement of piecemeal advances reported on posts in this blog and write up a new properly structured scientific paper which sets out the information in a better presentation, it will be more worthy of attention. Still, there is a strong link between elitism – which Dr Woit supports – and extremely complicated mathematical modelling which leads nowhere. String theory has been successfully hyped because – although it doesn’t exist [is not even wrong] at the scientific falsifiability hurdle – it
(a) does exist in popular stringy hype with all sorts of fairy tales of extra spatial dimensions with branes, sparticles, and so on, and
(b) does contain a lot of mathematics, which makes it look impressive.
‘It always bothers me that, according to the laws as we understand them today, it takes a computing machine an infinite number of logical operations to figure out what goes on in no matter how tiny a region of space, and no matter how tiny a region of time. How can all that be going on in that tiny space? Why should it take an infinite amount of logic to figure out what one tiny piece of spacetime is going to do? So I have often made the hypothesis that ultimately physics will not require a mathematical statement, that in the end the machinery will be revealed, and the laws will turn out to be simple, like the chequer board with all its apparent complexities.’
– R. P. Feynman, The Character of Physical Law, November 1964 Cornell Lectures, broadcast and published in 1965 by BBC, pp. 57-8.
Update (3 April 2009): Dr Woit on 1 April wrote a sarcastic post on his weblog “Not Even Wrong” called Origin of the World, about the pseudo-scientific hyping of mainstream general relativity-based cosmology by the University of Arizona with big-name experts who know everything and are really humble in telling us so,
“The event will be webcast, so the rest of the world can get the inside dope … Arizona is putting on quite a show, with a major effort to attract cutting-edge researchers in physics to the state, including the recent announcement of proposed new legislation.”
To be truthful, I read Dr Woit’s post on 1 April, visiting the link above, and didn’t realise it was an April fool’s joke because general relativity cosmologists are so crazy anyway this just looked like what they would be doing. He should be careful because when people claiming to be scientists believe in, and try to sell the world, a stringy landscape containing an infinite or large (10500) number of unseen parallel universes with 11 dimensions, with the anthropic principle selecting our universe, and claim to be scientists, it’s hard to make an April fool’s day joke about them which is recognised as such.
There is however a serious comment on the post by Joey Ramone:
Joey Ramone says:
April 2, 2009 at 10:30 am
P.S. Here is the video for Rock’n’Roll Cosmology Center: http://www.youtube.com/watch?v=DhRALq8IsL4
Towards the end of the video, the LHC is turned on and it
1) proves string theory
2) finds seven multiverses
3) locates 17 higher dimensions
4) proves the anthropic principle
5) creates baby black holes which become bouncing universes
6) explodes before any of this can be recorded
————————————————————
So I guess when the Nobel Prize committee read Joey’s comment, they’ll award Professors Ed Witten and Lenny Susskind a prize for string theory’s spin-2 graviton prediction and the anthropic landscape’s prediction that the constants of nature are suitable to allow life to exist in the universe where humans happen to exist. Cool science!
But there’s always the risk that this won’t ever happen and that the genius of Witten and Susskind on superstring will be censored and suppressed, and will therefore go totally unnoticed and unhyped by the sinister media such as Woit.
‘… I would note that history of science is full of theories which were initially considered crackpot (by some referee or even by entire communities), but broadly accepted at the end. It has been well documented at least 27 cases of future Nobel Laureates encountered resistance on part of scientific community towards their discoveries and instances in which 36 future Nobel Laureates encountered resistance on part of scientific journal editors or referees to manuscripts that dealt with discoveries that on later date would assure them the Nobel Prize. A beautiful example of last is the rejection letter to Hideki Yukawa by a referee of the Physical Review journal to be wrong in a number of important points: forces too small by a factor of 10-20, wrong spin dependence, etc. But his work was not wrong and, some years after, Yukawa received the Nobel Prize for that work.
‘Hermann Staudinger (Nobel Prize for Chemistry, 1953):
‘“It is no secret that for a long time many colleagues rejected your views which some of them even regarded as abderitic.”
‘Howard M. Temin (Nobel Prize for Physiology or Medicine, 1975):
‘“Since 1963-64, I had been proposing that the replication of RNA tumour viruses involved a DNA intermediate. This hypothesis, known as the DNA provirus hypothesis apparently contradicted the so-called ‘central dogma’ of molecular biology and met with a generally hostile reception…that the discovery took so many years might indicate the resistance to this hypothesis.” …
‘Among the more notorious instances of resistance to scientific discovery previous to existence of Nobels, we can cite the Mayer’s difficulties to publish a first version of the first law of thermodynamics. …’
‘… Sure, there are lots of examples in history of good scientific ideas being discounted and suppressed, but going on about those doesn’t have much to do with the case at hand.
‘I’ll leave Juan’s last rant up for a personal reason. The chemist Hermann Staudinger was my great-uncle.’
In a blog post about Einstein’s own ‘peer-review’ dispute with the Physical Review editor in 1936 (Einstein was so affronted by so-called ‘peer-review’ upon encountering it for the first time in 1936 with his error-containing first draft of a paper on gravity waves that he immediately complained ‘I see no reason to address the in any case erroneous comments of your anonymous expert. On the basis of this incident I prefer to publish the paper elsewhere’, withdrew his paper and never submitted to that journal again), Professor Sean Carroll (who has Feynman’s old desk in his office at California Institute of Technology) has amusingly written:
‘If there are any new Einsteins out there with a correct theory of everything all LaTeXed up, they should feel quite willing to ask me for an endorsement for the arxiv; I’d be happy to bask in the reflected glory and earn a footnote in their triumphant autobiography. More likely, however, they will just send their paper to Physical Review, where it will be accepted and published, and they will become famous without my help.
‘If, on the other hand, there is anyone out there who thinks they are the next Einstein, but really they are just a crackpot, don’t bother; I get things like that all the time. Sadly, the real next-Einsteins only come along once per century, whereas the crackpots are far too common.’
It’s amusing because Sean is claiming that he is:
1. better at spotting genuine work that Teller, Pauli, Bohr, Oppenheimer and others were at deciding Feynman’s work was nonsense at Pocono in 1948 (already discussed in detail in this post),
2. better than Pauli was when he dismissed the Yang-Mills theory in 1954 (already discussed in detail in this post), and generally
3. better than all the other ‘ignorant-in-the-new-idea but expert-in-frankly-obsolete-and-therefore-irrelevant-old-ideas’ critics of science.
Furthermore, he is assuming that anyone who wants to help science is really motivated by the desire for fame or its result, prizes. According to him, no censorship has ever really occurred in the world, because it would be illogical for anybody to censor a genuine advance! Seeing the history of the censorship of path integrals and Yang-Mills theory, building blocks of today’s field theories, Sean’s rant is just funny!
‘You are not the only person from an alternative perspective who purports to have a dramatic new finding, and here you are asking established scientists to take time out from conventional research to sit down and examine your claims in detail. Of course, we know that you really do have a breakthrough in your hands, while those people are just crackpots. But how do you convince everyone else? All you want is a fair hearing.
‘Scientists can’t possibly pay equal attention to every conceivable hypothesis, they would literally never do anything else. Whether explicitly or not, they typically apply a Bayesian prior to the claims that are put before them. Purported breakthroughs are not all treated equally; if something runs up against their pre-existing notions of how the universe works, they are much less likely to pay it any attention. So what does it take for the truly important discoveries to get taken seriously? … So we would like to present a simple checklist of things that alternative scientists should do in order to get taken seriously by the Man. And the good news is, it’s only three items! How hard can that be, really? True, each of the items might require a nontrivial amount of work to overcome. Hey, nobody ever said that being a lonely genius was easy. …
‘1. Acquire basic competency in whatever field of science your discovery belongs to. …
‘2. Understand, and make a good-faith effort to confront, the fundamental objections to your claims within established science. …
‘3. Present your discovery in a way that is complete, transparent, and unambiguous. …’
Duh! These three simple rules are just what Feynman and his acolyte Dyson, not to mention Yang and Mills, and all the others who were suppressed did! They are so obvious that everyone does spend a lot of time on these points before formulating a theory, while checking a theory, and when writing up the theory. Is Sean saying that Feynman, Dyson, Yang and Mills and everyone else was suppressed because they were ignorant of their field, ignored genuine objections, and were unclear? No, they were suppressed because of a basic flaw in human nature called fashion, which is exactly why Feynman later attacked fashion in science (after receiving his Nobel Prize in 1965, conveniently):
‘Science is the organized skepticism in the reliability of expert opinion.’ – R. P. Feynman (quoted by Smolin, The Trouble with Physics, 2006, p. 307).
‘The one thing the journals do provide which the preprint database does not is the peer-review process. The main thing the journals are selling is the fact that what they publish has supposedly been carefully vetted by experts. The Bogdanov story shows that, at least for papers in quantum gravity in some journals [including the U.K. Institute of Physics journal Classical and Quantum Gravity], this vetting is no longer worth much. … Why did referees in this case accept for publication such obviously incoherent nonsense? One reason is undoubtedly that many physicists do not willingly admit that they don’t understand things.’ – Peter Woit, Not Even Wrong, Jonathan Cape, London, 2006, p. 223.
The one thing mainstream people don’t admit to is being ignorant or heaven forbid wrong. This is why string theory is so popular, it doesn’t make a falsifiable prediction so it isn’t even wrong.
Basically, Sean Carroll’s advice to people censored is the ‘let them eat cake!’ advice that Queen Marie Antoinette allegedly gave when receiving complaints that people had no bread to eat. In other words, useless advice that is not only unhelpful but is also abusive in the sense that it implies that there is an obvious solution to a problem that the other person is too plain stupid to see for themselves. However, maybe I’m wrong about Sean and he is really a genius and a nice guy to boot!
Mainstream cosmology: the big bang is an observational fact with evidence behind it, but General Relativity’s Lambda-CDM is a religion
Aristarchus in 250 B.C. argued that the the earth rotates daily and orbits the sun annually. This was correct. But he was ignored for 17 centuries. In 150 A.D. the leading astronomer Ptolemy, author of a massive compendium on the stars, claimed to disprove Aristarchus’ solar system. If the earth was rotating towards the East, Ptolemy claimed, a person jumping up would always land to the West of the position the person jumped at! The earth would be rotating at about 1,000 miles per hour near the equator (circumference of Earth in miles divided into 24 hours). Therefore, to Ptolemy and his naive admirers (everybody), Aristarchus was disproved. In addition, Ptolemy claimed that clouds would appear to zoom around the sky at 1,000 miles/hour.
Ptolemy’s disproof was in error. But the funny thing is, nobody argued with it. They preferred to believe the Earth-centred cosmology of Ptolemy as it made more sense intuitively. Sometimes scientific facts are counter-intuitive. The error Ptolemy made was ignoring Newton’s first law of motion, inertia: standing on the earth, you are being carried towards the East as the Earth rotates and you continue to do so (because there is no mechanism to suddenly decelerate you!) when you jump up. So you continue going Eastwards with the rotating Earth while you are in the air. So does the air itself, which is why the clouds don’t lag behind the Earth’s rotation (the Coriolis acceleration is quite different!). French scientist Pierre Gassendi (1592-1655) dropped stones from the mast of a moving sail ship to test Ptolemy’s claim, and disproved it. The stones fell to the foot of the mast, regardless of whether the ship was moving or not.
Now let’s consider the false application of general relativity to cosmology. The big bang idea was proposed first by Erasmus Darwin, grandfather of the evolutionist, in his 1790 book ‘The Botanic Garden’:
‘It may be objected that if the stars had been projected from a Chaos by explosions, they must have returned again into it from the known laws of gravitation; this however would not happen, if the whole Chaos, like grains of gunpowder, was exploded at the same time, and dispersed through infinite space at once, or in quick succession, in every possible direction.’
The tragedy is that before evidence for the big bang came along, Einstein falsely believed that his general relativity – despite merely being a classical perturbative correction to classical physics which ignored quantum theory – would describe the universe.
Imagine what would have happened if the big bang had been discovered before general relativity! If general relativity had not been discovered by the time of Hubble’s 1929 discovery of redshifts correlating to distances, Gamow, Alpher and Hermann’s discovery in 1948 that the big bang would produce the observed amounts of hydrogen and helium in the universe, and the discovery of the redshifted heat flash of the big bang by Penzias and Wilson in 1965!
The spacetime dependence of light coming from great distances would have been studied more objectively, with the recognition that because we’re looking back in time as we look out to greater distances (due to the time taken for light to reach us), the Hubble law formulated as v = HR is misleading and is better stated as v = HcT, where T is the time past when the light was emitted.
Since c is the ultimate speed limit, setting v = c then gives you the age of the universe c = HcT thus T = 1/H. The age of the universe t for stars at distance R is then given by t = (1/H) – T, which rearranges to give us T = (1/H) – t. Inserting this into v = HcT,
v = HcT = Hc[(1/H) – t]
differentiating this gives us the acceleration of such receding matter
a = dv/dt = d{Hc[(1/H) – t]}/dt
= d[c – (Hct)]/dt
= –Hc
= -6 × 10-10 ms-2.
So cosmology would have predicted the acceleration of the universe based on observational facts! The tragedy of general relativity is that it confuses people into ad hoc modelling without quantum gravity, without mechanisms, with unexplained dark energy, and without falsifiable predictions. Once they predicted the acceleration, lacking general relativity’s infinitely adjustable pseudo-science they would have been able to apply empirical laws, Newton’s 2nd and 3rd laws of motion, to the acceleration of matter and thus predicted gravity quantitatively as I have shown. Hence, they would have had solid physics.
Just in case anyone reading this blog post disagrees with the Hubble recession law, see Ned Wright’s page linked here for the reasons why it is a fact, and if you need evidence for the basic facts of the big bang see the page linked here for a summary (unfortunately that page confuses speculative metrics of general relativity with the big bang theory, which doesn’t address quantum gravity in an expanding universe, but it does give some empirical data mixed in with the speculations required to fit general relativity to the facts). See Richard Lieu of the Physics Department, University of Alabama, ‘Lambda-CDM cosmology: how much suppression of credible evidence, and does the model really lead its competitors, using all evidence?’, http://arxiv.org/abs/0705.2462. (If you need evidence for other so-called ‘assumptions’ I use in ‘my theory’ which is not a theory but called a proof on this blog page, e.g. you think that say the formula for geometric area of a sphere or Newton’s F = ma is a speculation in a ‘theory’, then you simply need to learn basic mathematics and physics to understand which parts are fact and which – extra dimensions and so on – are speculative, and spend less time listening to stringers whose goal is to get research money for mixing up fact and fiction.)
The general-relativity-as-cosmology hype was started by Sir Arthur Eddington’s 1933 book The Expanding Universe (Pelican books, New York, 1940). The lesson of Ptolemy’s error is not that we must believe (without any proof) that the Earth is not in the centre of the universe; it is that fashion is not in the centre of the universe! Mainstream cosmologists derive the a conclusion from the error of Ptolemy which is diametrically opposed to scientific fact. They derive the conclusion that science is a religion which must believe the Earth is not in a special place, instead of deriving the conclusion that science is not a religion.
Hence, they merely change the religious belief objective instead of abandoning non-factual beliefs altogether: they substitute one prejudice for another prejudice, and start religiously believing that!
Professor Edward Harrison of the University of Arizona is religiously prejudiced in this way on pages 294-295 of his book, Cosmology: the Science of the Universe, 2nd ed., Cambridge University Press, London, 2000:
“… a bounded finite cloud of galaxies expanding at the boundary at the speed of light in an infinite static space restores the cosmic centre and the cosmic edge, and is contrary to modern cosmological beliefs.”
Who cares about f&%king modern cosmological beliefs? Science isn’t a fashion parade! Science isn’t a religion of believing that the Milky Way isn’t in a particular place. In any case, the major 3 mK anisotropy in the cosmic background radiation suggests that the Milky Way is nearly in the centre of the universe: it tells us the Milky Way has a speed relative to the cosmic background radiation emitted soon after the big bang, and that provides an order of magnitude estimate for the motion of the Milky Way matter since the big bang. Multiplying speed by age of universe, we get a distance which is a fraction of 1% of the horizon radius of the universe, suggesting we’re near the centre:
R. A. Muller, ‘The cosmic background radiation and the new aether drift’, Scientific American, vol. 238, May 1978, p. 64-74:
‘U-2 observations have revealed anisotropy in the 3 K blackbody radiation which bathes the universe. The radiation is a few millidegrees hotter in the direction of Leo, and cooler in the direction of Aquarius. The spread around the mean describes a cosine curve. Such observations have far reaching implications for both the history of the early universe and in predictions of its future development. Based on the measurements of anisotropy, the entire Milky Way is calculated to move through the intergalactic medium at approximately 600 km/s. It is noted that in a frame of reference moving with the original plasma emitted by the big bang, the blackbody radiation would have a temperature of 4500 K.’
Notice that I stated this in Electronics World and the only reaction I received was ignorance. One guy wrote an article – which didn’t even directly mention my article – in the same journal, claiming that the 3 mK anisotropy in the cosmic background radiation was too small to be accurately determined and should therefore be ignored! Duh! It is a massive anisotropy, detected by U2 aircraft back in the 70s, way bigger than the tiny anisotropy (the ripples which indicate the density fluctuations which are the basis for the formation of galaxy clusters in the early universe) discovered by the COBE microwave background explorer satellite with its liquid helium cold-load in 1992! The anisotropies in the cosmic background radiation were measured even more accurately by the WMAP satellite. It’s not ignored because it is inaccurate. It’s ignored due to religion/fashion:
‘The Michelson-Morley experiment has thus failed to detect our motion through the aether, because the effect looked for – the delay of one of the light waves – is exactly compensated by an automatic contraction of the matter forming the apparatus…. The great stumbing-block for a philosophy which denies absolute space is the experimental detection of absolute rotation.’ – Professor A.S. Eddington (who confirmed Einstein’s general theory of relativity in 1919), MA, MSc, FRS, Space Time and Gravitation: An Outline of the General Relativity Theory, Cambridge University Press, Cambridge, 1921, pp. 20, 152.
‘Popular accounts, and even astronomers, talk about expanding space. But how is it possible for space … to expand? … ‘Good question,’ says [Steven] Weinberg. ‘The answer is: space does not expand. Cosmologists sometimes talk about expanding space – but they should know better.’ [Martin] Rees agrees wholeheartedly. ‘Expanding space is a very unhelpful concept’.’ – New Scientist, 17 April 1993, pp32-3. (The volume of spacetime expands, but the fabric of spacetime, the gravitational field, flows around moving particles as the universe expands.)
‘Looking back at the development of physics, we see that the ether, soon after its birth, became the enfant terrible of the family of physical substances. … We shall say our space has the physical property of transmitting waves and so omit the use of a word we have decided to avoid. The omission of a word from our vocabulary is of course no remedy; the troubles are indeed much too profound to be solved in this way. Let us now write down the facts which have been sufficiently confirmed by experiment without bothering any more about the ‘e—r’ problem.’ – Albert Einstein and Leopold Infeld, Evolution of Physics, 1938, pp. 184-5. (This is a very political comment by them, and shows them acting in a very political – rather than purely scientific – light.)
‘The idealised physical reference object, which is implied in current quantum theory, is a fluid permeating all space like an aether.’ – Sir Arthur S. Eddington, MA, DSc, LLD, FRS, Relativity Theory of Protons and Electrons, Cambridge University Press, Cambridge, 1936, p. 180.
‘… the source of the gravitational field can be taken to be a perfect fluid…. A fluid is a continuum that “flows” … A perfect fluid is defined as one in which all antislipping forces are zero, and the only force between neighboring fluid elements is pressure.’ – Bernard Schutz, General Relativity, Cambridge University Press, 1986, pp89-90.
‘Some distinguished physicists maintain that modern theories no longer require an aether… I think all they mean is that, since we never have to do with space and aether separately, we can make one word serve for both, and the word they prefer is ‘space’.’ – A.S. Eddington, ‘New Pathways in Science’, v2, p39, 1935.
‘All charges are surrounded by clouds of virtual photons, which spend part of their existence dissociated into fermion-antifermion pairs. The virtual fermions with charges opposite to the bare charge will be, on average, closer to the bare charge than those virtual particles of like sign. Thus, at large distances, we observe a reduced bare charge due to this screening effect.’ – I. Levine, D. Koltick, et al., Physical Review Letters, v.78, 1997, no.3, p.424.
‘It seems absurd to retain the name ‘vacuum’ for an entity so rich in physical properties, and the historical word ‘aether’ may fitly be retained.’ – Sir Edmund T. Whittaker, A History of the Theories of the Aether and Electricity, 2nd ed., v1, p. v, 1951.
‘It has been supposed that empty space has no physical properties but only geometrical properties. No such empty space without physical properties has ever been observed, and the assumption that it can exist is without justification. It is convenient to ignore the physical properties of space when discussing its geometrical properties, but this ought not to have resulted in the belief in the possibility of the existence of empty space having only geometrical properties… It has specific inductive capacity and magnetic permeability.’ – Professor H.A. Wilson, FRS, Modern Physics, Blackie & Son Ltd, London, 4th ed., 1959, p. 361.
‘Scientists have thick skins. They do not abandon a theory merely because facts contradict it. They normally either invent some rescue hypothesis to explain what they then call a mere anomaly or, if they cannot explain the anomaly, they ignore it, and direct their attention to other problems. Note that scientists talk about anomalies, recalcitrant instances, not refutations. History of science, of course, is full of accounts of how crucial experiments allegedly killed theories. But such accounts are fabricated long after the theory had been abandoned. … What really count are dramatic, unexpected, stunning predictions: a few of them are enough to tilt the balance; where theory lags behind the facts, we are dealing with miserable degenerating research programmes. Now, how do scientific revolutions come about? If we have two rival research programmes, and one is progressing while the other is degenerating, scientists tend to join the progressive programme. This is the rationale of scientific revolutions. … Criticism is not a Popperian quick kill, by refutation. Important criticism is always constructive: there is no refutation without a better theory. Kuhn is wrong in thinking that scientific revolutions are sudden, irrational changes in vision. The history of science refutes both Popper and Kuhn: on close inspection both Popperian crucial experiments and Kuhnian revolutions turn out to be myths: what normally happens is that progressive research programmes replace degenerating ones.’ – Imre Lakatos, Science and Pseudo-Science, pages 96-102 of Godfrey Vesey (editor), Philosophy in the Open, Open University Press, Milton Keynes, 1974.
If he was writing today, maybe he would have to reverse a lot of that to account for the hype-type “success” of string theory ideas that fail to make definite (quantitative) checkable predictions, while alternatives are censored out completely.
No longer could Dr Lakatos claim that:
“What really count are dramatic, unexpected, stunning predictions: a few of them are enough to tilt the balance; where theory lags behind the facts, we are dealing with miserable degenerating research programmes.”
It’s quite the opposite. The mainstream, dominated by string theorists like Jacques Distler and others at arXiv, can actually stop “silly” alternatives from going on to arXiv and being discussed, as they did with me:
http://arxiv.org/help/endorsement –
‘We don’t expect you to read the paper in detail, or verify that the work is correct, but you should check that the paper is appropriate for the subject area. You should not endorse the author … if the work is entirely disconnected with current [string theory] work in the area.’
What serious researcher is going to treat quantum field theory objectively and work on the simplest possible mechanisms for a spacetime continuum, when it will result in their censorship from arXiv, their inability to find any place in academia to study such ideas, and continuous hostility and ill-informed “ridicule” from physically ignorant string “theorists” who know a lot of very sophisticated maths and think that gives them the authority to act as “peer-reviewers” and censor stuff from journals that they refuse to first read?
Sent: 02/01/03 17:47
Subject: Your_manuscript LZ8276 Cook
Physical Review Letters does not, in general, publish papers on alternatives to currently accepted theories.
Yours sincerely,
Stanley G. Brown, Editor,
Physical Review Letters
Now, why has this nice genuine guy still not published his personally endorsed proof of what is a “currently accepted” prediction for the strength of gravity? Will he ever do so?
“… in addition to the dimensionality issue, the string theory approach is (so far, in almost all respects) restricted to being merely a perturbation theory.”
– Sir Roger Penrose, The Road to Reality, Jonathan Cape, London, 2004, page 896.
Richard P. Feynman points out in The Feynman Lectures on Gravitation, page 30, that gravitons do not have to be spin-2, which has never been observed! Despite this, the censorship of the facts by mainstream “stringy” theorists persists, with professor Jacques Distler and others at arXiv believing with religious zeal that (1) the rank-2 tensors of general relativity prove spin-2 gravitons and (2) string theory is the only consistent theory for spin-2 gravitons, despite Einstein’s own warning shortly before he died:
‘I consider it quite possible that physics cannot be based on the [smooth geometric] field principle, i.e., on continuous structures. In that case, nothing remains of my entire castle in the air.’
– Albert Einstein in a letter to friend Michel Besso, 1954.
Sir Air Arthur Eddington versus Edward Milne
Sir Eddington’s book The Expanding Universe first popularized the major prejudice:
“For a model of the universe let us represent spherical space by a rubber balloon. Our three dimensions of length, breadth, and thickness ought all to lie on the skin of the balloon; but there is only room for two, so the model will have to sacrifice one of them. That does not matter very seriously. Imagine the galaxies to be embedded in the rubber. Now let the balloon be steadily inflated. That’s the expanding universe.”
(Eddington, quoted on page 294 of Harrison’s Cosmology, 2nd ed., Cambridge University Press, 2000. This statement can also be found on page 67 of the 1940 edition of The Expanding Universe, Pelican, New York.)
This confusion based on general relativity is wrong:
‘Popular accounts, and even astronomers, talk about expanding space. But how is it possible for space … to expand? … ‘Good question,’ says [Steven] Weinberg. ‘The answer is: space does not expand. Cosmologists sometimes talk about expanding space – but they should know better.’ [Martin] Rees agrees wholeheartedly. ‘Expanding space is a very unhelpful concept’.’ – New Scientist, 17 April 1993, pp32-3. (The volume of spacetime expands, but the fabric of spacetime, the gravitational field, flows around moving particles as the universe expands.)
The radial contraction (1/3)MG/c2 of spacetime around a mass (the Earth’s radius is contracted 1.5 mm as predicted by general relativity) is a real pressure effect from the quantum gravitons. General relativity attributes this to distortion by a fourth dimension (time, acting as an extra spatial dimension!) so that the radial contraction without transverse contraction (circumference contraction) doesn’t affect Pi. But you get a better physical understanding from quantum gravity, as explained on previous posts which treat this in detail as a quantum gravity effect: the pressure of gravitons squeezes masses. It also causes the Lorentz-FitzGerald contraction. You get the predictions of restricted and general relativity from quantum gravity, but without the mystery and religious manure.
Sir Eddington in The Expanding Universe (1933; reprinted by Pelican, new York, 1940) writes on page 21:
“The unanimity with which the galaxies are running away looks almost as though had a pointed aversion to us. We wonder why we should be shunned as though our system were a plague spot in the universe. But that is too hasty an inference, and there is really no reason to think that the animus is especially directed against our galaxy. … In a general dispersal or expansion every individual observes every other individual to be moving away from him. … We should therefore no longer regard the phenomenon as a movement away from our galaxy. It is a general scattering apart, having no particular centre of dispersal.”
Notice the sneaky way that Eddington moves from fact to speculative assertion: he has no evidence whatsoever that there is no centre of dispersal, he merely shows that that is one possibility. Yet – after showing that it is a possibility – he then claims that we should regard it as being the correct explanation, with no science to back up why he is selecting that explanation! But then he adds more honestly on the same page:
“I do not want to insist on these observational facts dogmatically. It is granted that there is a possibility of error or misinterpretation.”
On page 22 he writes:
“For the present I make no reference to any ‘expansion of space’. I am speaking of nothing more than the expansion or dispersal of a material system. Except for the large scale of the phenomenon the expansion of the universe is as commonplace as the expansion of a gas.”
On page 25 he writes about prejudice in science:
“A scientist commonly professes to base his beliefs on observations, not theories. Theories, it is said, are useful in suggesting new ideas and new lines of investigation for the experimenter; but ‘hard facts’ are the only proper ground for conclusion. I have never come across anyone who carries this profession into practice [Eddington never met me] – certainly not the hard-headed experimentalist, who is the more swayed by his theories because he is less accustomed to scrutinise them. Observation is not sufficient. We do not believe our eyes unless we are first convinced that what they appear to tell us is credible.”
On page 30 he writes about the effect of positive cosmological constant, positive lambda:
“It is a dispersive force like that which I imagined as scattering apart the audience in the lecture-room. Each thinks it is directed away from him. We may say that the repulsion has no centre, or that every point is a centre of repulsion.
“Thus in straightening out his law of gravitation to satisfy ideal conditions, Einstein almost inadvertently added a repulsive scattering force to the Newtonian attraction of bodies. We call this force the cosmological repulsion, for it depends on and is proportional to the cosmological constant. It is utterly imperceptible within the solar system or between the sun and neighbouring stars.
“But since it increases proportionately to the distance we have only to go far enough to find it appreciable, then strong, and ultimately overwhelming. In practical observation the farthest we have yet gone is 150 million light-years. Well within that distance we find that celestial objects are scattering apart as if under a repulsive force. Provisionally we conclude that here cosmological repulsion has become dominant and is responsible for the dispersion.
“We have no direct evidence [in 1933] of an outward acceleration of the nebulae, since it is only the velocities that we observe. But it is reasonable to suppose that the nebulae, individually as well as collectively, follow the rule – the greater the distance the faster the recession. If so, the velocity increases as the nebula recedes, so that there is an outward acceleration. Thus from the observed motions we can work backwards and calculate the repulsive force, and so determine observationally the cosmological constant lambda.”
On page 61, Eddington states:
“To suppose that velocity of expansion in the (fictitious) radial direction involves kinetic energy, may seem to be taking our picture of spherical space too literally; but the energy is so far real that it contributes to the mass of the universe. In particular a universe projected from B to reach A necessarily has greater mass than one which falls back without reaching the vertical (Einstein) position.
“Lemaitre does not share my idea of an evolution of the universe from the Einstein state. His theory of the beginning is a fireworks theory [big bang] – to use his own description of it. The world began with a violent projection from position B, i.e., from the state in which it was condensed to a point or atom; the projection was strong enough to carry it past the Einstein state, so that it is now falling down towards A as observation requires.”
Then on page 65 Eddington discusses Edward Milne’s work on the physics of the real big bang:
“E. A. Milne [Nature, 2 July 1932] has pointed out that if initially the galaxies, endowed with their present speeds, were concentrated in a small volume, those with highest speed would by now have travelled farthest. If gravitational and other forces are negligible, we obtain in this way a distribution in which speed and distance from the centre are proportional. Whilst accounting for the dependence of speed on distance, this hypothesis creates a new difficulty as to the occurrence of the speeds. To provide a moderately even distribution of nebulae up to 150 million light years distance, high speeds must be very much more frequent than low speeds; this peculiar anti-Maxwellian distribution of speeds becomes especially surprising when it is supposed to have occurred originally in a compact aggregation of galaxies.”
The error here is that the big bang is not a simple explosion: graviton exchange between fundamental particles of mass causes the accelerating expansion. It’s more curious that Eddington and Milne also seem to entirely neglect the fact that as we look to greater distances, we’re looking to earlier times in the universe, when the universe was more compressed and therefore of higher density! So it seems that Milne backed the common sense big bang idea, published in a mainstream journal Nature, but got the details wrong, pathing the way for general relativity to be preferred as an endlessly adjustable cosmological model. So on page 67 Eddington writes (as quoted above):
“For a model of the universe let us represent spherical space by a rubber balloon. Our three dimensions of length, breadth, and thickness ought all to lie on the skin of the balloon; but there is only room for two, so the model will have to sacrifice one of them. That does not matter very seriously. Imagine the galaxies to be embedded in the rubber. Now let the balloon be steadily inflated. That’s the expanding universe.”
He adds on pages 67-8:
“The balloon, like the universe, is under two opposing forces; so we may take the internal pressure tending to inflate it to correspond to the cosmological repulsion, and the tension of the rubber trying to contract it to correspond to the mutual attraction of the galaxies, although here the analogy is not very close.”
On page 103, Eddington popularises another speculation, namely the large numbers hypothesis, stating that the universe contains about 1079 atoms, a number which is about the square of the ratio of the electromagnetic force to gravitational force between two unit charges (electron and proton). However, he doesn’t provide a checkable theoretical connection, just numerology.
On page 111 he goes further into numerology by trying to find an ad hoc connection between the Sommerfeld dimensionless fine structure constant (137.036…) and the ratio of proton to electron mass, suggesting the two solutions for mass m to the quadratic equation 10m2 – 136m + 1 = 0 are in the ratio of the mass of the proton to the mass of the electron. The numbers 10 and 136 come from very shaky numerology (maybe we have 10 fingers so that explains 10, and 137 – 1 degree of freedom = 136). The result is not accurate when the latest data for the mass of the proton and electron are put into the equation. It worked much better with the now-obsolete data Eddington had available in 1932. On page 116 Eddington states:
“It would seem that the expansion of the universe is another one-way process parallel with the thermodynamical running-down [3rd law of thermodynamics]. One cannot help thinking that the two processes are intimately connected; but, if so, the connection has not yet been found.”
It’s obvious that the expansion of the universe islinked to the 3rd law of thermodynamics if you think as follows.
First, if the universe was static (not expanding), the radiation of energy by stars would lead to everywhere gradually reaching a thermal equilibrium, in which everything would have equal temperature. In this event, there would be “heat death” because no work would be possible: there would be no heat sink anywhere so you would be unable to transfer waste energy anywhere. The energy all around you would be useless because it could not be directed. You would no more be able to extract useful (work-causing) energy from that chaotic energy than you can extract power from the air molecules bombarding you randomly from all directions at 500 metres per second average speed all the time! You have to have an asymmetry to get energy to do useful work, and without a heat sink you get nowhere: energy doesn’t go anywhere or produce any effect you want. It just makes you too hot.
Second, considering the expansion of the universe: it prevents thermal equilibrium by ensuring that the heat every star radiates into space is redshifted and thus can’t be received by other stars with a power which is equal to the output of power by a star. The expansion of the universe therefore provides a heat sink, preventing thermal equilibrum and “heat death” predicted by the 3rd law of thermodynamics for a static universe.
In his conclusion on page 118, Eddington retreats from his earlier arrogant claims, stating:
“Science has its showrooms and its workshops. The public today, I think rightly, is not content to wander round the showrooms where the tested products are exhibited; the demand is to see what is going on in the workshops. You are welcome to enter; but do not judge what you see by the standards of the showroom.
“We have been going round a workshop in the basement of the building of science. The light is dim, and we stumble sometimes. About us is confusion and mess which there has not been time to sweep away. The workers and their machines are enveloped in murkiness. But I think that something is being shaped here – perhaps something rather big. I do not not quite know what it will be when it is completed and polished for the showroom. But we can look at the present designs and the novel tools that are being used in its manufacture; we can contemplate too the little successes which make us hopeful.”
This reminds you of the kind of political spin used by cranks to defend crackpot extradimensional stringy theory. Now we have finished looking at Eddington’s hype for a lambda-CDM general relativity metric of the expanding universe, let’s return to Professor Edward Harrison’s mainstream Cosmology: The Science of the Universe, 2nd ed., Cambridge University Press, 2000. There are some sections from pages 294 to 507 which are worth discussing. On page 294 Harrison states:
“The [expanding universe] debate began at a British Association science meeting in 1931 and was published as a collection of contributions in Nature under the title ‘The evolution of the universe.’ From this symposium Edward Milne emerged as a principal contributor … But Milne rejected general relativity and strenuously opposed the expanding space paradigm [matter recedes from other matter, but the fabric of space does not expand; it flows around moving fundamental particles and pushes in at the rear, giving a net inward motion of spacetime fabric – exerting a pressure causing gravity – when there is a net acceleration of matter radially away from the observer]. He refused to attribute to space … the properties of curvature and expansion. … Of the expanding space paradigm, he saidin 1934, ‘This concept, though mathematically significant, has by itself no physical content; it is merely the choice of a particular mathematical apparatus for describing and analyzing phenomena. An alternative procedure is to choose a static space, as in ordinary physics, and analyze the expansion phenomena as actual motions in this space’.”
It is this statement which infuriated Harrison into responding on the same page:
“… a bounded finite cloud of galaxies expanding at the boundary at the speed of light in an infinite static space restores the cosmic centre and the cosmic edge, and is contrary to modern cosmological beliefs.”
So, facts are contrary to modern pseudoscientific religious beliefs, so the facts must be ignored! Nice one, Harrison. Here’s another one on page 428:
“An explosion occurs at a point in space, whereas the big bang embraces all of space. In an explosion, gas is driven outward by a steep pressure gradient, and a large pressure difference exists between the centre and edge of the expanding gas. In the universe … no center and edge exist.”
Harrison has, you see, been throughout the entire universe and scientifically confirmed that “the big bang embraces all of space” and that there is no center and no edge. Wow! Hope he gets a Nobel Prize for his amazing discovery. Or maybe he will get the Templeton Prize for Religion instead? It’s hard to know what to do to discredit fashionable horsesh*t that is believed by many with religious zeal – but no evidence whatsoever – to be fact.
Notice that Harrison’s claim that an explosion has a steep pressure gradient bears no relation to the facts of explosions whatsoever: the 1.4 megaton Starfish nuclear test at 400 km altitude sent out its explosive energy as X-rays and radiation, and did not create any blast wave or pressure gradient. There was no sound from the explosion, just a flash of light and other radiation. For the full facts about the 1962 nuclear explosions in space, see my posts here, here, here and here. In a low altitude air burst, you get a pressure gradient, but in a high altitude explosion in space you don’t. Harrison is totally confused about explosions. Does he deny on religious grounds that supernova explosions are “explosions” and choose to call them something else instead? Sir Fred Hoyle, who named the “big bang” explosive universe, was a plain-talking Yorkshire man who believed in being clear. He wrote:
‘But compared with a supernova a hydrogen bomb is the merest trifle. For a supernova is equal in violence to about a million million million million hydrogen bombs all going off at the same time.’ – Sir Fred Hoyle (1915-2001), The Nature of the Universe, Pelican Books, London, 1963, p. 75.
Nuclear explosions are very helpful in understanding the world in general:
‘Dr Edward Teller remarked recently that the origin of the earth was somewhat like the explosion of the atomic bomb…’ – Dr Harold C. Urey, The Planets: Their Origin and Development, Yale University Press, New Haven, 1952, p. ix.
‘In fact, physicists find plenty of interesting and novel physics in the environment of a nuclear explosion. Some of the physical phenomena are valuable objects of research, and promise to provide further understanding of nature.’ – Dr Harold L. Brode, The RAND Corporation, ‘Review of Nuclear Weapons Effects,’ Annual Review of Nuclear Science, Volume 18, 1968, pp. 153-202.
‘It seems that similarities do exist between the processes of formation of single particles from nuclear explosions and formation of the solar system from the debris of a [7*1026 megatons of TNT equivalent type Ia] supernova explosion. We may be able to learn much more about the origin of the earth, by further investigating the process of radioactive fallout from the nuclear weapons tests.’ – Dr P. K. Kuroda, University of Arkansas, ‘Radioactive Fallout in Astronomical Settings: Plutonium-244 in the Early Environment of the Solar System,’ Radionuclides in the Environment (Dr E. C. Freiling, Symposium Chairman), Advances in Chemistry Series No. 93, American Chemical Society, Washington, D.C., 1970, pp. 83-96.
Copy of a comment to Arcadian Functor:
Thanks for that link:
“Theory Failure #1: In order to make string theory work on paper our four dimensional real world had to be increased to eleven dimensions. Since these extra dimensions can never be verified, they must be believed with religious-like faith — not science.
Theory Failure #2: Since there are an incalculable number of variations of the extra seven dimensions in string theory there are an infinite number of probable outcomes.
Theory Failure #3: The only prediction ever made by string theory — the strength of the cosmological constant — was off by a factor of 55, which is the difference in magnitude of a baseball and our sun.
Theory Failure #4: While many proponents have called string theory “elegant,” this is the furthest thing from the truth. No theory has ever proven as cumbrous and unyielding as string theory. With all of its countless permutations it has established itself to be endless not elegant.
Theory Failure #5: The final nail in the coffin of string theory is that it can never be tested.”
Point #2 is wrong and should say a landscape of 10^500 different universes result from the different compactifications of the 6-d manifold, not an incalculable number.
Failure #3 contains a typing error and should read 10^55 not 55. If string theory predicted the cosmological constant off by just a factor of 55, it would be hailed a success. (Interestingly I predicted the acceleration of the universe and hence CC accurately in 1996 and published it, but nobody wants to know because it’s not fashionable to build theory on facts!)
It’s becoming clear that string theory won’t die, and attacking it just leads to greater censorship of alternative ideas.
This is precisely because stringers defend themselves by suppressing alternatives, either by taking the funding and research students who would otherwise go into alternatives, or by directly deleting papers from arXiv as occurred to me, or by pretending to be “peers” of people working on alternative ideas so they can work as “peer-reviewers” and censor alternative ideas from journal publication simply for not being related to string theory. Then they are free to proclaim without the slightest embarrassment that no alternatives exist.
So there is no easy solution to this problem, and pointing out the problem accomplishes nothing. It’s like those people who pointed out that Hitler was up to no good in the 30s before war was declared. Such people were simply ignored.
‘Most people would think that someone who runs around saying they have a wondrous TOE that predicts amazing new things, but they’re not sure whether the amazing new things happen at the Planck scale or the scale of a galaxy, would have to be almost by definition a crackpot.’ – Dr Peter Woit, December 18, 2004 at 12:03 pm, http://www.math.columbia.edu/~woit/wordpress/?p=123&cpage=1#comment-1782
‘Peter and a large number of others, including myself, are looking for a specific predictions which can be tested with specific experiments. If you cannot advance any, then what you do does not deserve the label “physics”.’ – Dr Chris Oakley, December 18, 2004 at 2:20 pm, http://www.math.columbia.edu/~woit/wordpress/?p=123&cpage=1#comment-1779
‘Chris Oakley, you may be looking for unique exact predictions or whatever, but what you’re looking for is absolutely irrelevant for the question how Nature works. If there happens to be a cosmic superstring – macroscopic fundamental string, for example – 10,000 light years from the Sun, then it will become a fact of Nature and we will have to live with it – and scientists will have to give a proper explanation. If this turns out to be the case, it will be absolutely obvious that no one could have predicted this string in advance. … Let me emphasize once again that cynicism of sourballs like you, Chris Oakley, has no consequences for physics whatsoever. You’re just annoying and obnoxious, but your contributions to science are exactly zero. If you think that it is easy to make reliable and unique new predictions of phenomena beyond the Standard Model, try to compete with us.’ – String theorist [then an Assistant Professor of Physics at Harvard University] Dr Lubos Motl, December 18, 2004 at 2:59 pm, http://www.math.columbia.edu/~woit/wordpress/?p=123&cpage=1#comment-1778
‘People like Oakley should be dealt with by the US soldiers with the gun – and I am sort of ashamed to waste my time with such immoral idiots.’ – Dr Lubos Motl, December 19, 2004 at 10:11 am, http://www.math.columbia.edu/~woit/wordpress/?p=123&cpage=1#comment-1768
‘Peter:
‘What’s the point writting a letter to ARXIV? They already said they are not interested in your opinion. Predictable it will take another 3 months before you see any response and the only response you will get is that they ignore you.
‘And it is ridiculous for you to defend ARXIV for having to protect themselves against crackpots. They welcome the biggest crackpot of all, the super string theory. I know that till this day you are not willing to consider super string theory as a crackpot, and you still want to consider it as a science. The point is any theory that fails to make a useful prediction is considered crackpot. It doesn’t matter that string theorists are honestly making the effort to try to come up with a prediction. That is simply not good enough to differentiate their theory from crackpot. All crackpot theorists DO honestly hope for a useful prediction.
‘Until string theorists can show that they can make meaningful predictions, and that their prediction can be verified by experiments, I think it is fair and square that super string theory be classified as a crackpot theory. ARXIV therefore is a major crackpot depository.
‘You might as well instead write to New York Times, or any of the public media.’ – Quantoken, February 25, 2006 at 4:42 am, http://www.math.columbia.edu/~woit/wordpress/?p=353&cpage=1#comment-8765
‘We don’t expect you to read the paper in detail, or verify that the work is correct, but you should check that the paper is appropriate for the subject area. You should not endorse the author … if the work is entirely disconnected with current [string theory] work in the area.’ – http://arxiv.org/help/endorsement
‘They don’t want any really strong evidence of dissent. This filtering means that the arxiv reflects pro-mainstream bias. It sends out a powerful warning message that if you want to be a scientist, don’t heckle the mainstream or your work will be deleted.
‘In 2002 I failed to get a single brief paper about a crazy-looking yet predictive model on to arxiv via my university affiliation (there was no other endorsement needed at that time). In emailed correspondence they told me to go get my own internet site if I wasn’t contributing to mainstream [stringy] ideas.’ – nigel, February 24, 2006 at 5:26 am, http://www.math.columbia.edu/~woit/wordpress/?p=353&cpage=1#comment-8728
‘Witten has made numerous major contributions to string theory, most famously in 1995 after coming up with ideas which spawned a more general 11-dimensional framework called M-theory while on a flight from Boston to Princeton.
‘The 1980s and 90s were dotted with euphoric claims from string theorists. Then in 2006 Peter Woit of Columbia University in New York and Lee Smolin of the Perimeter Institute for Theoretical Physics in Waterloo, Canada, published popular books taking string theory to task for its lack of testability and its dominance of the job market for physicists. Witten hasn’t read either book, and compares the “string wars” surrounding their publication – which played out largely in the media and on blogs – to the fuss caused by the 1995 book The End of Science, which argued that the era of revolutionary scientific discoveries was over. “Neither the publicity surrounding that book nor the fact that people lost interest in talking about it after a while reflected any change in the intellectual underlying climate.”
‘Not that Witten would claim string theory to be trouble-free. He has spent much of his career studying the possible solutions that arise when projecting string theory’s 10 or 11 dimensions onto our 4D world. There is a vast number of possible ways to do this – perhaps 10500 by some counts. But a decade ago what seemed like a problem became a virtue in the eyes of many string theorists. Astronomers discovered that the expansion of the universe is accelerating. This suggests that what appears to us as empty space is in fact pervaded by a mysterious substance characterised by a concept dreamed up by Einstein called the “cosmological constant”.
‘Witten calls it the most shocking discovery since he’s been in the field. … Witten majored in history and then dabbled in economics before switching to mathematics and physics.’ – Matthew Chalmers, ‘Inside the tangled world of string theory’, New Scientist magazine issue 2703, 15 April 2009, http://www.newscientist.com/article/mg20227035.600-inside-the-tangled-world-of-string-theory.html
‘Aside from everything else, what exactly is the prediction that string theory made about RHIC?
‘That viscosity over entropy density (eta/s) is 1/4 pi? Well, this is not anymore a prediction (see, for example, http://arxiv.org/abs/0812.2521): eta/s in theories with string duals can go to lower values to 1/4pi, perhaps all the way to 0 (or quantum mechanics could prevent this. But this was known way before string theory (see, e.g. Physical Review, vol. D31, pp. 53-62, 1985).
‘That eta/s is “low” in a strongly coupled theory? Well, that’s a pretty obvious point that transcends string theory.
‘It is cute that AdS/CFT reproduces many phenomena also observed in hydrodynamics, but there is NO AdS/CFT result that can be sensibly compared with data and used to make a prediction. NONE. Not one. If anyone disagrees, please give an example.
‘AdS/CFT is, currently, a very interesting conceptual exercise. Perhaps tomorrow someone WILL extract predictions relevant to heavy ion collisions out of it. But it hasn’t happened yet. And to claim it has is dishonest Public Relations.’ – luny, April 16, 2009 at 4:52 am, http://www.math.columbia.edu/~woit/wordpress/?p=1817&cpage=1#comment-47974
‘The string theory side of AdS/CFT gives you gravity in 5 dimensional AdS space, not four dimensional space. For this and many other reasons you can’t use it for unification. The 4d physics of the theory is supposed to be N=4 SYM (no gravity), this may be a useful approximation to QCD, but it’s not a unified theory.
‘If you believe in much much more general conjectures about gauge duals of string theories in different “string vacua”, then you could imagine that there are gauge theory duals of the kind of string theory used in unification. These would be 3d gauge theories, and looking for them is an active field of research. As far as I can tell though, if it is successful, all you will get is a different parametrization of the “Landscape”, an infinite number of complicated qfts, corresponding to the infinite number of complicated “string vacua”.’ – Dr Peter Woit, April 16, 2009 at 9:45 am, http://www.math.columbia.edu/~woit/wordpress/?p=1817&cpage=1#comment-47978
‘“So if AdS CFT turns out to work correctly it would be a good argument for string theory. Is this not true?”
‘But does it work correctly? In a recent discussion here, I became aware of the paper arXiv:0806.0110v2. Therein, the following statements are proven:
‘1. AdS/CFT makes a prediction for some quantities c’/c and k’/k, eqn (5).
‘2. This prediction is compared to the exactly known values for the 3D O(n) model at n = infinity, eqns (28) and (30).
‘3. The values disagree. Perhaps not by so much, but they are not exactly right.
‘This may be expressed by saying that the d-dimensional O(n) model does not have a gravitational dual (an euphemism for “AdS/CFT screwed up”?), at least not in some neighborhood of n = infinity, d = 3, and hence not for generic n and d. There might be exceptional cases where a gravitational dual exist, e.g. the line d = 2, but generically it seems disproven by the above result. In particular, I find it unlikely that the 3D Ising, XY and Heisenberg models (n = 1, 2, 3) can be treated with AdS/CFT.’ – Thomas Larsson, April 16, 2009 at 1:33 pm, http://www.math.columbia.edu/~woit/wordpress/?p=1817&cpage=1#comment-47983
‘What I see as a big negative coming out of string theory is the ideology that the way to unify particle physics and gravity is via a 10/11d string/M-theory. This is the idea that I think has completely failed. Not only has it led to nothing good, it has led a lot of the field into bad pseudo-science (anthropics, the landscape, the multiverse…), and this has seriously damaged the reputation of the whole subject.
‘… people keep publicly pushing the same failed idea, discrediting the subject completely. In the process they have somehow managed to discredit the whole idea of using sophisticated mathematics to investigate QFT and string theory at a truly deep level, convincing people that this was a failure caused by not being “physical” enough. Instead, it was a failure of a specific, “physical” idea: that you can get a unified theory by changing from quantum fields to strings.
‘If you want concrete suggestions for what to work on, note that we don’t understand the electroweak theory non-perturbatively at all. There are all sorts of questions about non-perturbative QFT that we don’t understand. Sure, these are not easy problems, but then again, all the problems in string theory are now supposed to be too hard, why not instead work on QFT problems that are too hard?’ – Dr Peter Woit, April 13th, 2009 at 2:49 pm, http://blogs.discovermagazine.com/cosmicvariance/2009/04/09/string-wars-the-aftermath/#comment-71663
‘The problem with your [Peter Woit] book and blog is that they do not offer any way of making progress – all they do is call for a shutdown of string theory (which as you yourself admit above, has lead to useful things). What do you recommend as a better, concrete, alternate way of making progress? Lets hear it, dammit.’ – jamie, April 13th, 2009 at 1:03 pm
‘“jamie” … If you want concrete suggestions for what to work on, note that we don’t understand the electroweak theory non-perturbatively at all. There are all sorts of questions about non-perturbative QFT that we don’t understand. Sure, these are not easy problems, but then again, all the problems in string theory are now supposed to be too hard, why not instead work on QFT problems that are too hard? Personally I’m currently fascinated by the BRST formalism.’ – Peter Woit, April 13th, 2009 at 2:49 pm
‘And about your research advice for me: don’t you think it is more prudent if I took advice from somebody who has, you know, actually made it in academia???’ – jamie, April 13th, 2009 at 4:40 pm
‘First Jamie asks Dr Woit for advice, Dr Woit gives the requested advice, then Jamie says he doesn’t want advice from Dr Woit! It’s funny to see rhetorical questions backfire when answered honestly. Everytime a string theorist asks what alternative ideas there are to work on (as a rhetorical question, the implicit message being ‘string theory is only game in town’), they have to be abusive to the alternative ideas they receive in reply.’ – April 16th, 2009 at 9:24 am, http://blogs.discovermagazine.com/cosmicvariance/2009/04/09/string-wars-the-aftermath/#comment-72004
‘If you look at the history of any failed speculative idea about physics, what you’ll find is that the proponents of the failed idea rarely publicly admit that it’s wrong. Instead they start making excuses about how it could still be right, but it’s just too hard to make progress. … This is what is happening to the speculative idea of string-based unification.’ – Peter Woit, April 13th, 2009 at 8:42 am, http://blogs.discovermagazine.com/cosmicvariance/2009/04/09/string-wars-the-aftermath/#comment-71626
‘Some cases I was thinking of are:
‘1. Heisenberg’s unified field theory
‘2. Chew’s S-matrix theory of the strong interactions
‘3. Cold fusion
‘2. is a complicated story interrelated with string theory. But, one aspect of the story is that in 1973-74 it became clear that QCD was the correct theory of the strong interactions, but there were quite a few people who for the next decade wouldn’t admit this. With AdS/CFT, some of the string theory ideas that grew out of this period did get connected to gauge theory and turned out to be useful. By analogy, I think it’s entirely possible that in the future some very different way of thinking about string theory and unification will have something to do with reality. The problem is that all known ways of doing this have failed, and that’s something proponents are not willing to admit.’ – Peter Woit,
April 13th, 2009 at 10:09 am, http://blogs.discovermagazine.com/cosmicvariance/2009/04/09/string-wars-the-aftermath/#comment-71640
Gauge symmetry: whenever the motion or charge or angular momentum of spin, or some other symmetry, is altered, it is a consequence of conservation laws for momentum and energy in physics that radiation is emitted or received. This is Noether’s theorem, which was applied to quantum physics by Weyl, giving the concept of gauge symmetry. Fundamental interactions are modelled by Feynman diagrams of scattering between gauge bosons or ‘virtual radiation’ (virtual photons, gravitons, etc.) and charges (electric charge, mass, etc.). The Feynman diagrams are abstract, and doesn’t represent the gauge bosons as taking any time to travel between charges (massless radiations travel at light velocity). Two extra polarizations (giving a total of 4-polarizatins!) have to be added to the 2-polarization observed photon on the mainstream model of quantum electrodynamics, to make it produce attractive forces between dissimilar charges. This is an ad hoc modification, similar to changing the spin of the graviton to spin-2 to ensure universal attraction between similar gravitational charge (mass/energy). If you look at the physics more carefully, you find that the spin of the graviton is actually spin-1 and gravity is a repulsive effect: we’re exchanging gravitons (as repulsive scatter-type interactions) more forcefully with the immense masses of receding galaxies above us than we are with the masses in hemisphere of the universe below us because of the Earth’s slight attenuation of gravitons, so the resultant is a downward acceleration. What’s impressive about this is that it makes checkable predictions including the strength (coupling G) of gravity and many other things (see calculations below), unlike string ‘theory’ which is a spin-2 graviton framework that leads to 10500 different predictions (so vague it could be made to fit anything that nature turns out to be, but makes no falsifiable predictions, i.e. junk science). When you look at electromagnetism more objectively, the virtual photons carry an additional polarization in the form of a net electric charge (positive or negative). This again leads to checkable predictions for the strength of electromagnetism and other things. The most important single correct prediction, however, was the acceleration of the universe, due to the long-distance repulsion between large masses in the universe mediated by spin-1 gravitons. This was published in 1996 and confirmed by observations in 1998 published in Nature by Saul Perlmutter et al., but it is still censored out by charlatans such as string ‘theorists’ (quotes are around that word because it is no genuine scientific theory, just a landscape of 10500 different speculations).
Typical string theory deception: ‘String theory has the remarkable property of predicting gravity.’ (E. Witten, ‘Reflections on the Fate of Spacetime’, Physics Today, April 1996.)
Actually what he means but can’t be honest enough to say is that string theory in 10/11 dimensions is compatible with a false spin-2 graviton speculation. Let’s examine the facts:
Above: Spin-1 gravitons causing apparent “attraction” by repulsion, the “attraction” being due to similar charges being pushed together by repulsion from massive amounts of similar sign gravitational charges in the distant surrounding universe.
Nearby gravitational charges don’t exchange gravitons forcefully enough to compensate for the stronger exchange with converging gravitons coming in from immense masses (clusters of galaxies at great distances, all over the sky), due to the physics discussed below, so their graviton interaction cross-section effectively shields them on facing sides. Thus, they get pushed together. This is what we see as gravity.
By wrongly ignoring the rest of the mass in the universe and focussing on just a few masses (right hand side of diagram), Pauli and Fierz in the 1930s falsely deduced that for similar signs of gravitational charges (all gravitational charge so far observed falls the same way, downwards, so all known mass/energy has similar gravitational charge sign, here arbitrarily represented by “-” symbols, just to make an analogy to negative electric charge to make the physics easily understood), spin-1 gauge bosons can’t work because they would cause gravitational charges to repel! So they changed the graviton spin to spin-2, to “fix it”.
This mechanism proves that a spin-2 graviton is wrong; instead the spin-1 graviton does the job of both ‘dark energy’ (the outward acceleration of the universe, due to repulsion of similar sign gravitational charges over long distances) and gravitational ‘attraction’ between relatively small, relatively nearby masses which get repelled more towards one another due to distant masses in the universe than they are repelling one another!

Above: Spin-1 gauge bosons for fundamental interactions. In each case the surrounding universe interacts with the charges, a vital factor ignored in existing mainstream models of quantum gravity and electrodynamics.
The massive versions of the SU(2) Yang-Mills gauge bosons are the weak field quanta which only interact with left-handed particles. One half (corresponding to exactly one handedness for weak interactions) of SU(2) gauge bosons acquire mass at low energy; the other half are the gauge bosons of electromagnetism and gravity. (This diagram is extracted from the more detailed discussion and calculations made below in the more detailed treatment; which is vital for explaining how massless electrically charged bosons can propagate as exchange radiation while they can’t propagate – due to infinite magnetic self-inductance – on a one-way path. The exchange of electrically charged massless bosons in two directions at once along each path – which is what exchange amounts to – means that the curls of the magnetic fields due to the charge from each oppositely-directed component of the exchange will cancel out the curl of the other. This means that the magnetic self-inductance is effectively zero for massless charged radiation being endlessly exchanged from charge A to charge B and back again, even though it infinite and thus prohibited for a one way path such as from charge A to charge B without a simultaneous return current of charged massless bosons. This was suggested by the fact that something analogous occurs in another area of electromagnetism.)
Masses are receding due to being knocked apart by gravitons which cause cosmological-scale repulsion between masses as already explained (pushing distant galaxies apart and also pushing nearby masses together). The inward force, presumably mediated by spin-1 gravitons, from a receding mass m at distance occurs because mass accelerating away from us has an outward force due to Newton’s 2nd law (F = ma), and an equal and opposite (inward) reaction force mediated by gravitons under Newton’s 3rd law (action and reaction are equal and opposite). If its mass m is small, then the inward force of gravitons (being exchanged), which is directed towards you from that small nearby mass, is trivial. So the shielding effect of a nearby small mass (like the planet Earth) slightly shields the gravitons exchange radiation from immense distant masses in the hemisphere of the universe below you (half the mass of the universe), instead of adding to it (the planet Earth isn’t receding from you). So very large masses beyond the Earth (distant receding galaxies) are sending in a large inward force due to their large distance and mass: an extremely small fraction these spin-1 gravitons effectively interact with the Earth by scattering back off the graviton scatter cross-sectional area of some of the fundamental particles in the Earth. So small nearby masses are pressed together, because nearby, non-receding particles with mass cause an asymmetry (a reduction in the graviton field being received from more distant masses in that particular direction), so be pushed towards each other. This gives an inverse-square law force and it uniquely also gives an accurate prediction for the gravitational parameter G as proved later in this post.
When you push two things together using field quanta such as those from the electrons on the surface of your hands, the resulting motions can be modelled as an attractive effect, but it is clearly caused by the electrons in your hands repelling those on the surface of the other object. We’re being pushed down by the gravitational repulsion of immense distant masses distributed around us in the universe, which causes not just the cosmological acceleration over large distances, but also causes gravity between relatively small, relatively nearby masses by pushing them together. (In 1996 the spin-1 quantum gravity proof given below in this post was inspired by an account of the ‘implosion’ principle, used in all nuclear weapons now, whereby the inward-directed half of the force of an explosion of a TNT shell surrounding a metal sphere compresses the metal sphere, making the nuclei in that sphere approach one another as though there was some contraction.)
Notice that in the universe the fact that we are surrounded by a lot of similar-sign gravitational charge (mass/energy) at large distances will automatically cause the accelerative expansion of the universe (predicted accurately by this gauge theory mechanism in 1996, well before Perlmutter’s discovery confirming the predicted acceleration/’dark energy’), as well as causing gravity, and uses spin-1. It doesn’t require the epicycle of changing the graviton spin to spin-2. Similar gravitational charges repel, but because there is so much similar gravitational charge at long distances from us with the gravitons converging inwards as they are exchanged with an apple and the Earth, the immense long range gravitational charges of receding galaxies and galaxy clusters repel a two small nearby masses together harder than they repel one another apart! This is why they appear to attract.
This is an error for the reason (left of diagram above) that spin-1 only appears to fail when you ignore the bulk of the similar sign gravitational charge in the universe surrounding you. If you stupidly ignore that surrounding mass of the universe, which is immense, then the simplest workable theory of quantum gravity necessitates spin-2 gravitons!
The best presentation of the mainstream long-range force model (which uses massless spin-2 gauge bosons for gravity and massless spin-1 gauge bosons for electromagnetism) is probably chapter I.5, Coulomb and Newton: Repulsion and Attraction, in Professor Zee’s book Quantum Field Theory in a Nutshell (Princeton University Press, 2003), pages 30-6. Zee uses an approximation due to Sidney Coleman, whereby you have to work through the theory assuming that the photon has a real mass m, to make the theory work, but at the end you set m = 0. (If you assume from the beginning that m = 0, the simple calculations don’t work, so you then need to work with gauge invariance.)
Zee starts with a Langrangian for Maxwell’s equations, adds terms for the assumed mass of the photon, then writes down the Feynman path integral, which is ò DAeiS(A) where S(A) is the action, S(A) = ò d4xL, where L is the Lagrangian based on Maxwell’s equations for the spin-1 photon (plus, as mentioned, terms for the photon having mass, to keep it relatively simple and avoid including gauge invariance). Evaluating the effective action shows that the potential energy between two similar charge densities is always positive, hence it is proved that the spin-1 gauge boson-mediated electromagnetic force between similar charges is always repulsive. So it works mathematically.
A massless spin-1 boson has only two degrees of freedom for spinning, because in one dimension it is propagating at velocity c and is thus ‘frozen’ in that direction of propagation. Hence, a massless spin-1 boson has two polarizations (electric field and magnetic field). A massive spin-1 boson, however, can spin in three dimensions and so has three polarizations.
Moving to quantum gravity, a spin-2 graviton will have 22 + 1 = 5 polarizations. Writing down a 5 component tensor to represent the gravitational Lagrangian, the same treatment for a spin-2 graviton then yields the result that the potential energy between two lumps of positive energy density (mass is always positive) is always negative, hence masses always attract each other.
This has now hardened into a religious dogma or orthodoxy which is used to censor the facts of the falsifiable, predictive spin-1 graviton mechanism as being ‘weird’. Even Peter Woit and Lee Smolin, who recognise that string theory’s framework for spin-2 gravitons isn’t experimentally confirmed physics, still believe that spin-2 gravitons are right!
Actually, the amount of spin-1 gravitational repulsion force between two small nearby masses is completely negligible, and it takes immense masses in the receding surrounding universe (galaxies, clusters of galaxies, etc., surrounding us in all directions) to produce the force we see as gravity. The fact that gravity is not cancelled out is due to the fact that it comes with one charge sign only, instead of coming in equal and opposite charges like electric charge. This is the reason why we have to include the gravitational charges in the surrounding universe in the mechanism of quantum gravity, while in electromagnetism it is conventional orthodoxy to ignore surrounding electric charges which come in opposite types which appear to cancel one another out. There is definitely no such cancellation of gravitational charges from surrounding masses in the universe, because there is only one kind of gravitational charge observed (nobody has seen a type of mass which falls upward, so all gravitational charge observed has the same charge!). So we have to accept a spin-1 graviton, not a spin-2 graviton, as being the simplest theory (see the calculations below that prove it predicts the observed strength for gravitation!), and spin-1 gravitons lead somewhere: the spin-1 graviton neatly fits gravity into a modified, simplified form of the Standard Model of particle physics!
‘If no superpartners at all are found at the LHC, and thus supersymmetry can’t explain the hierarchy problem, by the Arkani-Hamed/Dimopoulos logic this is strong evidence for the anthropic string theory landscape. Putting this together with Lykken’s argument, the LHC is guaranteed to provide evidence for string theory no matter what, since it will either see or not see weak-scale supersymmetry.’ – Not Even Wrong blog post, ‘Awaiting a Messenger From the Multiverse’, July 17th, 2008.
It’s kinda nice that Dr Woit has finally come around to grasping the scale of the terrible, demented string theory delusion in the mainstream, and can see that nothing he writes affects the victory to be declared for string theory, regardless of what data is obtained in forthcoming experiments! His position and that of Lee Smolin and other critics is akin to the dissidents of the Soviet Union, traitors like Leon Trotsky and nuisances like Andrei Sakharov. They can maybe produce minor embarrassment and irritation to the Evil Empire, but that’s all. The general opinion of string theorists to his writings is that it’s inevitable that someone should complain, and they go on hyping string theory. The public will go on ignoring the real quantum gravity facts. Dr Woit writes:
‘For the last eighteen years particle theory has been dominated by a single approach to the unification of the Standard Model interactions and quantum gravity. This line of thought has hardened into a new orthodoxy that postulates an unknown fundamental supersymmetric theory involving strings and other degrees of freedom with characteristic scale around the Planck length[…] It is a striking fact that there is absolutely no evidence whatsoever for this complex and unattractive conjectural theory. There is not even a serious proposal for what the dynamics of the fundamental ‘M-theory’ is supposed to be or any reason at all to believe that its dynamics would produce a vacuum state with the desired properties. The sole argument generally given to justify this picture of the world is that perturbative string theories have a massless spin two mode and thus could provide an explanation of gravity, if one ever managed to find an underlying theory for which perturbative string theory is the perturbative expansion.
‘This whole situation is reminiscent of what happened in particle theory during the 1960’s, when quantum field theory was largely abandoned in favor of what was a precursor of string theory. The discovery of asymptotic freedom in 1973 brought an end to that version of the string enterprise and it seems likely that history will repeat itself when sooner or later some way will be found to understand the gravitational degrees of freedom within quantum field theory.
‘While the difficulties one runs into in trying to quantize gravity in the standard way are well-known, there is certainly nothing like a no-go theorem indicating that it is impossible to find a quantum field theory that has a sensible short distance limit and whose effective action for the metric degrees of freedom is dominated by the Einstein action in the low energy limit. Since the advent of string theory, there has been relatively little work on this problem, partly because it is unclear what the use would be of a consistent quantum field theory of gravity that treats the gravitational degrees of freedom in a completely independent way from the standard model degrees of freedom. One motivation for the ideas discussed here is that they may show how to think of the standard model gauge symmetries and the geometry of space-time within one geometrical framework.
‘Besides string theory, the other part of the standard orthodoxy of the last two decades has been the concept of a supersymmetric quantum field theory. Such theories have the huge virtue with respect to string theory of being relatively well-defined and capable of making some predictions. The problem is that their most characteristic predictions are in violent disagreement with experiment. Not a single experimentally observed particle shows any evidence of the existence of its “superpartner”.’
– P. Woit, Quantum Field Theory and Representation Theory: A Sketch (2002), http://arxiv.org/abs/hep-th/0206135, p. 52.
But notice that Dr Woit was convinced in 2002 that a spin-2 graviton would explain gravity. More recently he has become less hostile to supersymmetric theories, for example by conjecturing that spin-2 supergravity without string theory may be what is needed:
‘To go out on a limb and make an absurdly bold guess about where this is all going, I’ll predict that sooner or later some variant (”twisted”?) version of N=8 supergravity will be found, which will provide a finite theory of quantum gravity, unified together with the standard model gauge theory. Stephen Hawking’s 1980 inaugural lecture will be seen to be not so far off the truth. The problems with trying to fit the standard model into N=8 supergravity are well known, and in any case conventional supersymmetric extensions of the standard model have not been very successful (and I’m guessing that the LHC will kill them off for good). So, some so-far-unknown variant will be needed. String theory will turn out to play a useful role in providing a dual picture of the theory, useful at strong coupling, but for most of what we still don’t understand about the SM, it is getting the weak coupling story right that matters, and for this quantum fields are the right objects. The dominance of the subject for more than 20 years by complicated and unsuccessful schemes to somehow extract the SM out of the extra 6 or 7 dimensions of critical string/M-theory will come to be seen as a hard-to-understand embarassment, and the multiverse will revert to the philosophers.’
Evidence
As explained briefly above, there’s a fine back of the envelope calculation – allegedly proving that a spin-2 graviton is needed for universal attraction – in the mainstream accounts, as exemplified by Zee’s online sample chapter from his ‘Quantum Field Theory in a Nutshell’ book (section 5 of chapter 1). But when you examine that kind of proof closely, it just considers two masses exchanging gravitons with one another, which ignores two important aspects of reality:
1. there are far more than two masses in the universe which are always exchanging gravitons, and in fact the majority of the mass is in the surrounding universe; and
2. when you want a law for the physics of how gravitons are imparting force, you find that only receding masses forcefully exchange gravitons with you, not nearby masses. Perlmutter’s observed acceleration of the universe gives receding matter outward force by Newton’s second law, and gives a law for gravitons: Newton’s third law gives an equal inward-directed force, which by elimination of the possibilities known in the Standard Model and quantum gravity, must be mediated by gravitons. Nearby masses which aren’t receding have outward acceleration of zero and so produce zero inward graviton force towards you for their graviton-interaction cross-sectional area. So they just act as a shield for gravitons coming from immense masses beyond them, which produces an asymmetry, so you get pushed towards non-receding masses while being pushed away from highly redshifted masses.
It’s tempting for people to dismiss new calculations without checking them, just because they are inconsistent with previous calculations such as those allegedly proving the need for spin-2 gravitons (maybe combined with the belief that “if the new idea is right, somebody else would have done it before”; which is of course a brilliant way to stop all new developments in all areas by everybody …).
The deflection of a photon by the sun is by twice the amount predicted for the theory of a non-relativistic object (say a slow bullet) fired along the same (initial) trajectory. Newtonian theory says all objects fall, as does this theory (gravitons may presumably interact with energy via unobserved Higgs field bosons or whatever, but that’s not unique for spin-1, it’s also going to happen with spin-2 gravitons). The reason why a photon is deflected twice the amount that Newton’s law predicts is that a photon’s speed is unaffected by gravity unlike the case of a non-relativistic object which speeds up as it enters stronger gravitational field regions. So energy conservation forces the deflection to increase due to the gain in gravitational potential energy, which in the case of a photon is used entirely for deflection (not speed changes).
In general relativity this is a result of the fact that the Ricci tensor isn’t directly proportional to the stress energy tensor because the divergence of the stress energy tensor isn’t zero (which it should be for conservation of mass-energy). So from the Ricci tensor, half the product of the metric tensor and the trace of the Ricci tensor must be subtracted. This is what causes the departure from Newton’s law in the deflection of light by stars. Newton’s law omits conservation of mass-energy, a problem which is clear when it’s expressed in tensors. General relativity corrects this error. If you avoid assuming Newton’s law and obtain the correct theory direct from quantum gravity, this energy conservation issue doesn’t arise.
Spin 2 graviton exchanges between 2 masses cause attraction.
Spin 1 graviton exchanges between 2 masses cause repulsion.
Spin 1 graviton exchanges between all masses will push 2 nearby masses together.
Similarly if you had two protons nearby and surrounded them with a spherical shell of immense positive charge, they might be pushed together. (Another example is squeezing two things together: the electrons in your hand repel the things, but that doesn’t stop the two things being pushed together as if there is ‘attraction’ occurring between them.) This is what is occurs when spin-1 gravitons cause gravity by pushing things together locally. Gauge bosons are virtual particles, but they still interact to cause forces!
String theory is widely hailed for being compatible with the spin-2 graviton widely held to be true because for universal attraction between two similar charges (all masses and all energy falls the same way in a gravitational field, so it all has similar gravitational charge) you need a gauge boson which has spin-2. This argument is popularized by Professor Zee in section 5 of chapter 1 of his textbook Quantum Field Theory in a Nutshell. It’s completely false because we simply don’t live in a universe with two gravitational charges. There are more than two particles in the universe. The path integral that Zee and others do assume explicitly only two masses are involved in the gravitational interactions which cause gravity.
If you correct this error, the repulsion of similar charges cause gravity by pushing two nearby masses together, just as on large scales it pushes matter apart causing the accelerating expansion of the universe.
There was a sequence of comments on the Not Even Wrong blog post about Awaiting a Messenger From the Multiverse concerning the spin of the graviton (some of which have been deleted since for getting off topic). Some of these comments have been retrieved from my browser history cache and are below. There was an anonymous comment by ‘somebody’ at 5:57 am on 20 July 2008 stating:
‘Perturbative string theory has something called conformal invariance on the worldsheet. The empirical evidence for this is gravity. The empirical basis for QFT are locality, unitarity and Lorentz invariance. Strings manage to find a way to tweak these, while NOT breaking them, so that we can have gravity as well. This is oft-repeated, but still extraordinary. The precise way in which we do the tweaking is what gives rise to the various kinds of matter fields, and this is where the arbitrariness that ultimately leads to things like the landscape comes in. … It can easily give rise to things like multiple generations, non-abelain gauge symmetry, chiral fermions, etc. some of which were considered thorny problems before. Again, constructing PRECISELY our matter content has been a difficult problem, but progress has been ongoing. … But the most important reason for liking string theory is that it shows the features of quantum gravity that we would hope to see, in EVERY single instance that the theory is under control. Black hole entropy, gravity is holographic, resolution of singularities, resolution of information paradox – all these things have seen more or less concrete realizations in string theory. Black holes are where real progress is, according to me, but the string phenomenologists might disagree. Notice that I haven’t said anything about gauge-gravity duality (AdS/CFT). Thats not because I don’t think it is important, … Because it is one of those cases where two vastly different mathematical structures in theoretical physics mysteriously give rise to the exact same physics. In some sense, it is a bit like saying that understanding quantum gravity is the same problem as understanding strongly coupled QCD. I am not sure how exciting that is for a non-string person, but it makes me wax lyrical about string theory. It relates black holes and gauge theories. …. You can find a bound for the viscosity to entropy ratio of condensed matter systems, by studying black holes – thats the kind of thing that gets my juices flowing. Notice that none of these things involve far-out mathematical m***********, this is real physics – or if you want to say it that way, it is emprically based. … String theory is a large collection of promising ideas firmly rooted in the emprirical physics we know which seems to unify theoretical physics …’
To which anon. responded:
‘No it’s not real physics because it’s not tied to empirical facts. It selects an arbitary number of spatial extra dimensions in order to force the theory to give the non-falsifiable agreement with existing speculations about gravity, black holes, etc. Gravity and black holes have been observed but spin-2 gravitons and the detailed properties of black holes aren’t empirically confirmed. Extra spatial dimensions and all the extra particles of supersymmetries like supergravity haven’t been observed. Planck scale unification is again a speculation, not an empirical observation. The entire success of string theory is consistency with speculations, not with nature. It’s built on speculations, not upon empirical facts. Further, it’s not even an ad hoc model that can replace the Standard Model, because you can’t use experimental data to identify the parameters of string theory, e.g., the moduli. It’s worse therefore than ad hoc models, it can’t incorporate let alone predict reality.’
Anon. should have added that the AdS/CFT correspondence is misleading. [AdS/CFT correspondence work, with strong interactions being modelled by anti-de Sitter space with a negative (rather than positive) cosmological constant is misleading. People should be modelling phenomena by accurate models, not returning physics to the days when guys were arguing that epicycles are a clever invention and modelling the solar system using a false model (planets and stars orbiting the Earth in circles within circles) is a brilliant state of the art calculational method! (Once you start modelling phenomenon A using a false approximation from theory B, you’re asking for trouble because you’re mixing up fact and fiction. E.g., if a prediction fails, you have a ready-made excuse to simply add further epicycles/fiddles to ‘make it work’.) See my comment at http://kea-monad.blogspot.com/2008/07/ninja-prof.html]
somebody Says:
July 20th, 2008 at 10:42 am
Anon
The problems we are trying to solve, like “quantizing gravity” are already speculative by your standards. I agree that it is a reasonable stand to brush these questions off as “speculation”. But IF you consider them worthy of your time, then string theory is a game you can play. THAT was my claim. I am sure you will agree that it is a bit unreasonable to expect a non-speculative solution to a problem that you consider already speculative.
Incidentally, I never said a word about supersymmetry and Planck scale unification in my post because it was specifically a response to a question on the empirical basis of string theory. So I would appreciate it if you read my posts before taking off on rants, stringing cliches, .. etc. It was meant for the critics of string theory who actually have scientific reasons to dislike it, and not gut-reactions.
anon. Says:
July 20th, 2008 at 11:02 am
‘The problems we are trying to solve, like “quantizing gravity” are already speculative by your standards.’
Wrong again. I never said that. Quantizing gravity is not speculative by my standards, it’s a problem that can be addressed in other ways without all the speculation involved in the string framework. That’s harder to do than just claiming that string theory predicts gravity and then using lies to censor out those working on alternatives.
‘Incidentally, I never said a word about supersymmetry and Planck scale unification in my post because it was specifically a response to a question on the empirical basis of string theory.’
Wrong, because I never said that you did mention them. The reason why string theory is not empirical is precisely because it’s addressing these speculative ideas that aren’t facts.
‘It was meant for the critics of string theory who actually have scientific reasons to dislike it, and not gut-reactions.’
If you want to defend string as being empirically based, you need to do that. You can’t do so, can you?
somebody Says:
July 20th, 2008 at 11:19 am
‘Quantizing gravity is not speculative by my standards,’
Even though the spin 2 field clearly is.
My apologies Peter, I truly couldn’t resist that.
anon. Says:
July 20th, 2008 at 11:53 am
The spin-2 field for gravity is based on the false speculation that gravitons are exchanged purely between the attracting bodies. (To get universal attraction, such field quanta can be shown to require a spin of 2.) This speculation is contrary to the general principle that every body is a source of gravity. You never have gravitons exchanged merely between two masses in the universe. They will be exchanged between all the masses, and there is a lot of mass surrounding us at long distances.
There is no disproof which I’m aware of that the graviton has a spin of 1 and operates by pushing masses together. At least this theory doesn’t have to assume that there are only two gravitating masses in the universe which exchange gravitons!
somebody Says:
July 20th, 2008 at 12:20 pm
‘The spin-2 field for gravity is based on the false speculation that gravitons are exchanged purely between the attracting bodies. This speculation is contrary to the general principle that every body is a source of gravity.’
How many gravitationally “repelling” bodies do you know?
Incidentally, even if there were two kinds of gravitational charges, AND the gravitational field was spin one, STILL there are ways to test it. Eg: I would think that the bending of light by the sun would be more suppressed if it was spin one than if it is spin two. You need two gauge invariant field strengths squared terms to form that coupling, one for each spin one field, and that might be suppressed by a bigger power of mass or something. Maybe I am wrong about the details (i haven’t thought it through), but certainly it is testable.
somebody Says:
July 20th, 2008 at 12:43 pm
One could have only repelling bodies with spin one, but NOT only attractive ones. Because attractive requires opposite charges.
anon. Says:
July 20th, 2008 at 6:51 pm
‘How many gravitationally “repelling” bodies do you know?’
This repulsion between masses is very well known. Galaxies are accelerating away from every other mass. It’s called the cosmic acceleration, discovered in 1998 by Perlmutter. … F=ma then gives outward force of accelerating matter, and the third law of motion gives us equal inward force. All simple stuff. … Since this force is apparently mediated by spin-1 gravitons, the gravitational force of repulsion from one relatively nearby small mass to another is effectively zero. … the exchange of gravitons only produces a repulsive force over large distances from a large mass, such as a distant receding galaxy. This is why two relatively nearby (relative in cosmological sense of many parsecs) masses don’t repel, but are pushed together because they repel the very distant masses in the universe.
‘One could have only repelling bodies with spin one, but NOT only attractive ones. Because attractive requires opposite charges.’
As already explained, there is a mechanism for similar charges to ‘attract’ by repulsion if they are surrounded by a large amount of matter that is repelling them towards one another. If you push things together by a repulsive force, the result can be misinterpreted as attraction…
*******************************************************************
After this comment, ‘somebody’ (evidently a string supporter who couldn’t grasp physics) then gave a list issues he/she had about this comment. Anon. then responded to each:
anon. Says:
July 20th, 2008 at 6:51 pm
‘1. The idea of “spin” arises from looking for reps. of local Lorentz invariance. At the scales of the expanding universe, you don’t have local Loretz invarince.’
There are going to be graviton exchanges whether they are spin 1 or spin 2 or whatever, between distant receding masses in the expanding universe. So if this is a problem it’s a problem for spin-2 gravitons just as it is for spn-1. I don’t think you have any grasp of physics at all.
‘2. … The expanding background is a solution of the underlying theory, whatever it is. The generic belief is that the theory respects Lorentz invariance, even though the solution breaks it. This could of course be wrong, …’
Masses are receding from one another. The assumption that they are being carried apart on a carpet of expanding spacetime fabric which breaks Lorentz invariance is just a classical GR solution speculation. It’s not needed if masses are receding due to being knocked apart by gravitons which cause repulsion between masses as already explained (pushing distant galaxies apart and also pushing nearby masses together).
‘3. … For spin 1 partciles, this gives an inverse square law. In particular, I don’t see how you jumped … to the claim that the graviton is spin 1.’
… there will be very large masses beyond that nearby mass (distant receding galaxies) sending in a large inward force due to their large distance and mass. These spin-1 gravitons will presumably interact with the mass by scattering back off the graviton scatter cross-section for that mass. So a nearby, non-receding particle with mass will cause an asymmetry in the graviton field being received from more distant masses in that direction, and you’ll be pushed towards it. This gives an inverse-square law force.
‘4. You still have not provided an explanation for how the solar system tests of general relativity can survive in your spin 1 theory. In particular the bending of light. Einstein’s theory works spectacularly well, and it is a local theory. We know the mass of the sun, and we know that it is not the cosmic repulsion that gives rise to the bending of light by the sun.’
The deflection of a photon by the sun is by twice the amount predicted for the theory of a non-relativistic object (say a slow bullet) fired along the same (initial) trajectory. Newtonian theory says all objects fall, as does this theory (gravitons may presumably interact with energy via unobserved Higgs field bosons or whatever, but that’s not unique for spin-1, it’s also going to happen with spin-2 gravitons). The reason why a photon is deflected twice the amount that Newton’s law predicts is that a photon’s speed is unaffected by gravity unlike the case of a non-relativistic object which speeds up as it enters stronger gravitational field regions. So energy conservation forces the deflection to increase due to the gain in gravitational potential energy, which in the case of a photon is used entirely for deflection (not speed changes).
In general relativity this is a result of the fact that the Ricci tensor isn’t directly proportional to the stress energy tensor because the divergence of the stress energy tensor isn’t zero (which it should be for conservation of mass-energy). So from the Ricci tensor, half the product of the metric tensor and the trace of the Ricci tensor must be subtracted. This is what causes the departure from Newton’s law in the deflection of light by stars. Newton’s law omits conservation of mass-energy, a problem which is clear when it’s expressed in tensors. GR corrects this error. If you avoid assuming Newton’s law and obtain the correct theory direct from quantum gravity, this energy conservation issue doesn’t arise.
‘5. The problems raised by the fact that LOCALLY all objects attract each other is still enough to show that the mediator cannot be spin 1.’
I thought I’d made that clear;
Spin 2 graviton exchanges between 2 masses cause attraction.
Spin 1 graviton exchanges between 2 masses cause repulsion.
Spin 1 graviton exchanges between all masses will push 2 nearby masses together.
This is because the actual graviton exchange force causing repulsion in the space between 2 nearby masses is totally negligible (F = mrH^2 with small m and r terms) compared to the gravitons pushing them together from surrounding masses at great distances (F = mrH^2 with big receding mass m at big distance r).
Similarly if you had two protons nearby and surrounded them with a spherical shell of immense positive charge, they might be pushed together. (Another example is squeezing two things together: the electrons in your hand repel the things, but that doesn’t stop the two things being pushed together as if there is ‘attraction’ occurring between them.) This is what is occurs when spin-1 gravitons cause gravity by pushing things together locally. Gauge bosons are virtual particles, but they still interact to cause forces!
somebody Says:
July 21st, 2008 at 3:35 am
Now that you have degenerated to weird theories and personal attacks, I will make just one comment about a place where you misinterpret the science I wrote and leave the rest alone. I wrote that expanding universe cannot be used to argue that the graviton is spin 1. You took that to mean “… if this is a problem it’s a problem for spin-2 gravitons just as it is for spn-1.”
The expanding universe has nothing to do with the spin of the particle was my point, not that it can be used to argue for this or that spin. Spin arises from local Lorentz invariance.
anon. Says:
July 21st, 2008 at 4:21 am
‘The expanding universe has nothing to do with the spin of the particle was my point, not that it can be used to argue for this or that spin.’
Spin-1 causes repulsion. The universe’s expansion is accelerating. I’ve never claimed that particle spin is caused by the expansion of the universe. I’ve stated that repulsion is evident in the acceleration of the universe.
If you want to effectively complain about degeneration into weird theories and personal attacks, try looking at string theory more objectively. 10^500 universes, 10 dimensions, spin-2 gravitons, etc. (plus the personal attacks of string theorists on those working on alternative ideas).
***********************************
This shows that calculations based on checkable physics are vital in physics, because they are something that can be checked for consistency with nature. In string theory, so far there is no experimental possible, so all of the checks done are really concerned with internal (mathematical) consistency, and consistency with speculations of one kind or another. String theorist Professor Michio Kaku summarises the spiritual enthusiasm and hopeful religious basis for the string theory belief system as follows in an interview with the ‘Spirituality’ section of The Times of India, 16 July 2008, quoted in a comment by someone on the Not Even Wrong weblog (notice that Michio honestly mentions ‘… when we get to know … string theory…’, which is an admission that it’s not known because of the landscape problem of 10^500 alternative versions with different quantitative predictions; at present it’s not a scientific theory but rather 10^500):
‘… String theory can be applied to the domain where relativity fails, such as the centre of a black hole, or the instant of the Big Bang. … The melodies on these strings can explain chemistry. The universe is a symphony of strings. The “mind of God” that Einstein wrote about can be explained as cosmic music resonating through hyperspace. … String theory predicts that the next set of vibrations of the string should be invisible, which can naturally explain dark matter. … when we get to know the “DNA” of the universe, i.e. string theory, then new physical applications will be discovered. Physics will follow biology, moving from the age of discovery to the age of mastery.’
As with the 200+ mechanical aether theories of force fields existing the 19th century (this statistic comes from Eddington’s 1920 book Space Time and Gravitation), string theory at best is just a model for unobservables. Worse, it comes in 10^500 quantitatively different versions, worse than the 200 or so aethers of the 19th century. The problems with theorising about the physics at the instant of the big bang and the physics in the middle of a black hole is that you can’t actually test it. Similar problems exist when explaining dark matter because your theory contains invisible particles whose masses you can’t predict beyond saying they’re beyond existing observations (religions similarly have normally invisible angels and devils, so you could equally use religions to ‘explain dark matter’; it’s not a quantitative prediction in string theory so it’s not really a scientific explanation, just a belief system). Unification at the Planck scale and spin-2 gravitons are both speculative errors.
Once you remove all these the errors from string theory, you are left with something that is no more impressive than aether: it claims to be a model of reality and explain everything, but you don’t get any real use from it for predicting experimental results because there are so many versions it’s just too vague to be a science.It doesn’t connect well with anything in the real world at all. The idea that at least it tells us what particle cores are physically (vibrating loops of extradimensional ’string’) doesn’t really strike me as being science. People decide which version of aether to use by artistic criteria like beauty or fitting the theory to observations and arguing that if the aether was different from this or that version we wouldn’t exist to observe it’s consequences (the anthropic selection principle), instead of using factual scientific criteria: there are no factual successes of aether to evaluate. So it falls into the category of a speculative belief system, not a piece of science.
By Mach’s principle of economy, speculative belief systems are best left out of science until they can be turned into observables, useful predictions, or something that is checkable. Science is not divine revelation about the structure of matter and the universe, instead it’s about experiments and related fact-based theorizing which predicts things that can be checked.
**************************************************
Update: If you look at what Dr Peter Woit has done in deleting comments, he’s retained the one from anon which states:
‘[string is] not real physics because it’s not tied to empirical facts. It selects an arbitary number of spatial extra dimensions in order to force the theory to give the non-falsifiable agreement with existing speculations about gravity, black holes, etc. Gravity and black holes have been observed but spin-2 gravitons and the detailed properties of black holes aren’t empirically confirmed. Extra spatial dimensions and all the extra particles of supersymmetries like supergravity haven’t been observed. Planck scale unification is again a speculation, not an empirical observation. The entire success of string theory is consistency with speculations, not with nature. It’s built on speculations, not upon empirical facts. Further, it’s not even an ad hoc model that can replace the Standard Model, because you can’t use experimental data to identify the parameters of string theory, e.g., the moduli. It’s worse therefore than ad hoc models, it can’t incorporate let alone predict reality.’
Although he has kept that, Dr Woit deleted the further discussion comments about the spin 1 versus spin 2 graviton physics, as being off-topic. Recently he argued that supergravity (a spin-2 graviton theory) in low dimensions was a good idea (see post about this by Dr Tommaso Dorigo), so he is definitely biased in favour of the graviton having a spin of 2, despite that being not ‘not even wrong’ but plain wrong for reasons given above. If we go look at Dr Woit’s post ‘On Crackpotism and Other Things’, we find Dr Woit stating on January 3rd, 2005 at 12:25 pm:
‘I had no intention of promulgating a general theory of crackpotism, my comments were purely restricted to particle theory. Crackpotism in cosmology is a whole other subject, one I have no intention of entering into.’
If that statement by Dr Woit still stands, then facts from cosmology about the accelerating expansion of the universe presumably won’t be of any interest to him, in any particle physics context such as graviton spin. In that same ‘On Crackpotism and Other Things’ comment thread, Doug made a comment at January 4th, 2005 at 5:51 pm stating:
‘… it’s usually the investigators labeled “crackpots” who are motivated, for some reason or another, to go back to the basics to find what it is that has been ignored. Usually, this is so because only “crackpots” can afford to challenge long held beliefs. Non-crackpots, even tenured ones, must protect their careers, pensions and reputations and, thus, are not likely to go down into the basement and rummage through the old, dusty trunks of history, searching for clues as to what went wrong. …
‘Instead, they keep on trying to build on the existing foundations, because they trust and believe that …
‘In other words, it could be that it is an interpretation of physical concepts that works mathematically, but is physically wrong. We see this all the time in other cases, and we even acknowlege it in the gravitational area where, in the low limit, we interpret the physical behavior of mass in terms of a physical force formulated by Newton. When we need the accuracy of GR, however, Newton’s physical interpretation of force between masses changes to Einstein’s interpretation of geometry that results from the interaction between mass and spacetime.’
Doug commented on that ‘On Crackpotism and Other Things’ post at January 1st, 2005 at 1:04 pm:
‘I’ve mentioned before that Hawking characterizes the standard model as “ugly and ad hoc,” and if it were not for the fact that he sits in Newton’s chair, and enjoys enormous prestige in the world of theoretical physics, he would certainly be labeled as a “crackpot.” Peter’s use of the standard model as the criteria for filtering out the serious investigator from the crackpot in the particle physics field is the natural reaction of those whose career and skills are centered on it. The derisive nature of the term is a measure of disdain for distractions, especially annoying, repetitious, and incoherent ones.
‘However, it’s all too easy to yield to the temptation to use the label as a defense against any dissent, regardless of the merits of the case of the dissenter, which then tends to convert one’s position to dogma, which, ironically, is a characteristic of “crackpotism.” However, once the inevitable flood of anomalies begins to mount against existing theory, no one engaged in “normal” science, can realistically evaluate all the inventive theories that pop up in response. So, the division into camps of innovative “liberals” vs. dogmatic “conservatives” is inevitable, and the use of the excusionary term “crackpot” is just the “defender of the faith” using the natural advantage of his position on the high ground.
‘Obviously, then, this constant struggle, especially in these days of electronically enhanced communications, has nothing to do with science. If those in either camp have something useful in the way of new insight or problem-solving approaches, they should take their ideas to those who are anxious to entertain them: students and experimenters. The students are anxious because the defenders of multiple points of view helps them to learn, and the experimenters are anxious because they have problems to solve.
‘The established community of theorists, on the other hand, are the last whom the innovators ought to seek to convince because they have no reason to be receptive to innovation that threatens their domains, and clearly every reason not to be. So, if you have a theory that suggests an experiment that Adam Reiss can reasonably use to test the nature of dark energy, by all means write to him. Indeed, he has publically invited all that might have an idea for an experiment. But don’t send your idea to [cosmology professor] Sean Carroll because he is not going to be receptive, even though he too publically acknowledged that “we need all the help we can get” (see the Science Friday archives).’
GAUGE THEORIES
Whenever the motion or charge or angular momentum of spin, or some other symmetry, is altered, it is a consequence of conservation laws in physics that radiation is emitted or received. This is Noether’s theorem, which was applied to quantum physics by Weyl. Noether’s theorem (discovered 1915) connects the symmetry of the action of a system (the integral over time of the Lagrangian equation for the energy of a system) with conservation laws. In quantum field theory, the Ward-Takahashi identity expresses Noether’s theorem in terms of the Maxwell current (a moving charge, such as an electron, can be represented as an electric current since that is the flow of charge). Any modification to the symmetry of the current involves the use of energy, which (due to conservation of energy) must be represented by the emission or reception of photons, e.g. field quanta. (For an excellent introduction to the simple mathematics of the Lagrangian in quantum field theory and its role in symmetry modification for Noether’s theorem, see chapter 3 of Ryder’s Quantum Field Theory, 2nd ed., Cambridge University Press, 1996.)
So, when the symmetry of a system such as a moving electron is modified, such a change of the phase of an electron’s electromagnetic field (which together with mass is the only feature of the electron that we can directly observe) is accompanied by a photon interaction, and vice-versa. This is the basic gauge principle relating symmetry transformations to energy conservation. E.g., modification to the symmetry of the electromagnetic field when electrons accelerate away from one another implies that they emit (exchange) virtual photons.
All fundamental physics is of this sort: the electromagnetic, weak and strong interactions are all examples of gauge theories in which symmetry transformations are accompanied by the exchange of field quanta. Noether’s theorem is pretty simple to grasp: if you modify the symmetry of something, the act of making that modification involves the use or release of energy, because energy is conserved. When the electron’s field undergoes a local phase change to its symmetry, a gauge field quanta called a ’virtual photon’ is exchanged. However, it is not just energy conservation that comes into play in symmetry. Conservation of charge and angular momentum are involved in more complicated interactions. In the Standard Model of particle physics, there are three basic gauge symmetries, implying different types of field quanta (or gauge bosons) which are radiation exchanged when the symmetries are modified in interactions:
1. Electric charge symmetry rotation. This describes the electromagnetic interaction. This is supposedly the most simple gauge theory, the Abelian U(1) electromagnetic symmetry group with one element, invoking just one charge and one gauge boson. To get negative charge, a positive charge is represented as travelling backwards in time, and vice-versa. The gauge boson of U(1) is mixed up with the neutral gauge boson of SU(2), to the amount specified by the empirically based Weinberg mixing angle, producing the photon and the neutral weak gauge boson. U(1) represents not just electromagnetic interactions but also weak hypercharge.
The U(1) maths is based on a type of continuous group defined by Sophus Lie in 1873. Dr Woit summarises this very clearly in Not Even Wrong (UK ed., p47): ‘A Lie group … consists of an infinite number of elements continuously connected together. It was the representation theory of these groups that Weyl was studying.
‘A simple example of a Lie group together with a representation is that of the group of rotations of the two-dimensional plane. Given a two-dimensional plane with chosen central point, one can imagine rotating the plane by a given angle about the central point. This is a symmetry of the plane. The thing that is invariant is the distance between a point on the plane and the central point. This is the same before and after the rotation. One can actually define rotations of the plane as precisely those transformations that leave invariant the distance to the central point. There is an infinity of these transformations, but they can all be parametrised by a single number, the angle of rotation.

Argand diagram showing rotation by an angle on the complex plane. Illustration credit: based on Fig. 3.1 in Not Even Wrong.
‘If one thinks of the plane as the complex plane (the plane whose two coordinates label the real and imaginary part of a complex number), then the rotations can be thought of as corresponding not just to angles, but to a complex number of length one. If one multiplies all points in the complex plane by a given complex number of unit length, one gets the corresponding rotation (this is a simple exercise in manipulating complex numbers). As a result, the group of rotations in the complex plane is often called the ‘unitary group of transformations of one complex variable’, and written U(1).
‘This is a very specific representation of the group U(1), the representation as transformations of the complex plane … one thing to note is that the transformation of rotation by an angle is formally similar to the transformation of a wave by changing its phase [by Fourier analysis, which represents a waveform of wave amplitude versus time as a frequency spectrum graph showing wave amplitude versus wave frequency by decomposing the original waveform into a series which is the sum of a lot of little sine and cosine wave contributions]. Given an initial wave, if one imagines copying it and then making the copy more and more out of phase with the initial wave, sooner or later one will get back to where one started, in phase with the initial wave. This sequence of transformations of the phase of a wave is much like the sequence of rotations of a plane as one increases the angle of rotation from 0 to 360 degrees. Because of this analogy, U(1) symmetry transformations are often called phase transformations. …
‘In general, if one has an arbitrary number N of complex numbers, one can define the group of unitary transformations of N complex variables and denote it U(N). It turns out that it is a good idea to break these transformations into two parts: the part that just multiplies all of the N complex numbers by the same unit complex number (this part is a U(1) like before), and the rest. The second part is where all the complexity is, and it is given the name of special unitary transformations of N (complex) variables and denotes SU(N). Part of Weyl’s achievement consisted in a complete understanding of the representations of SU(N), for any N, no matter how large.
‘In the case N = 1, SU(1) is just the trivial group with one element. The first non-trivial case is that of SU(2) … very closely related to the group of rotations in three real dimensions … the group of special orthagonal transformations of three (real) variables … group SO(3). The precise relation between SO(3) and SU(2) is that each rotation in three dimensions corresponds to two distinct elements of SU(2), or SU(2) is in some sense a doubled version of SO(3).’
2. Isospin symmetry rotation. This describes the weak interaction of quarks, controlling the transformation of quarks within one family of quarks. E.g., in beta decay a neutron decays into a proton by the transformation of a downquark into an upquark, and this transformation involves the emission of an electron (conservation of charge) and an antineutrino (conservation of energy and angular momentum). Neutrinos were a falsifiable prediction made by Pauli on 4 December 1930 in a letter to radiation physicists in Tuebingen based on the spectrum of beta particle energies in radioactive decay (‘Dear Radioactive Ladies and Gentlemen, I have hit upon a desperate remedy regarding … the continous beta-spectrum … I admit that my way out may seem rather improbable a priori … Nevertheless, if you don’t play you can’t win … Therefore, Dear Radioactives, test and judge.’ – Pauli’s letter, quoted in footnote of page 12, http://arxiv.org/abs/hep-ph/0204104). The total amount of radiation emitted in beta decay could be determined from the difference in mass between the beta radioactive material and its decay product, the daughter material. The amount of energy carried in readily detectable ionizing beta particles could be measured. However, the beta particles were emitted with a continuous spectrum of energies up to a maximum upper energy limit (unlike the line spectra of gamma ray energies): it turned out that the total energy lost in beta decay was equal to the upper limit of the beta energy spectrum, which was three times the mean beta particle energy! Hence, on the average, only one-third of the energy loss in beta decay was accounted for in the emitted beta particle energy.
Pauli suggested that the unobserved beta decay energy was carried by neutral particles, now called antineutrinos. Because they are weakly interacting, it takes a great intensity of beta decay in order to detect the antineutrinos. They were first detected in 1956 coming from intense beta radioactivity in the fission product waste of a nuclear reactor. By conservation laws, Pauli had been able to predict the exact properties to be expected. The beta decay theory was developed soon after Pauli’s suggestion in the 1930s by Enrico Fermi, who then invented the nuclear reactor used to discover the antineutrino. However, Fermi’s theory has a neutron decay directly into a beta particle plus an antineutrino, whereas in the 1960s the theory of beta decay had to be expressed in terms of quarks. Glashow, Weinberg and Salam discovered that to make it a gauge theory there had to be a massive intermediate ‘weak gauge boson’. So what really happens is more complicated than in Fermi’s theory of beta decay. A downquark interacts with a massive W– weak field gauge boson, which then decays into an electron and an antineutrino. The massiveness of the field quanta is needed to explain the weak strength of beta decay (i.e., the relatively long half-lives of beta decay, e.g. a free neutron is radioactive and has a beta half life of 10.3 minutes, compared with the tiny lifetimes of a really small fraction of a second for hadrons which decay via the strong interaction). The massiveness of the weak field quanta was a falsifiable prediction, and in 1983 CERN discovered the weak field quanta with the predicted energies, confirming SU(2) weak interaction gauge theory.
There are two relative types or directions of isospin, by analogy to ordinary spin in quantum mechanics (where spin up and spin down states are represented by +1/2 and –1/2 in units of h-bar). These two isospin charges are modelled by the Yang-Mills SU(2) symmetry, which has (2*2)-1 = 3 gauge bosons (with positive, negative and neutral electric charge, respectively). Because the interaction is weak, the gauge bosons must be massive and as a result they have a short range, since massive virtual particles don’t exist for long in the vacuum, and can’t travel far in that short life time. The two isospin charge states allow quark-antiquark pairs, or doublets, to form, called mesons. The weak isospin force only acts on particles with left-handed spin. At high energy, all weak gauge bosons will be massless, allowing weak and electromagnetic forces become symmetric and unify. But at low energy, the weak gauge bosons acquire mass, supposedly from a Higgs field, breaking the symmetry. This Higgs field has not been observed, and the general Higgs models don’t predict a single falsifiable prediction (there are several possibilities).
3. Colour symmetry rotation. This changes the colour charge of a quark, in the process releasing colour charged gluons as the field quanta. Strong nuclear interactions (which bind protons into a nucleus against very strong electromagnetic repulsion, which would be expected to make nuclei explode in the absence of this strong binding force) are described by quantum chromodynamics, whereby quarks have a symmetry due to their strong nuclear or ‘colour’ charges. This originated with Gell-Mann’s SU(3) eightfold way of arranging the known baryons by their properties, a scheme which successfully predicted the existence of the Omega Minus in before it was experimentally observed in 1964 at Brookhaven National Laboratory, confirming the SU(3) symmetry of hadron properties. The understanding (and testing) of SU(3) as a strong interaction Yang-Mills gauge theory in terms of quarks with colour charges and gluon field quanta was a completely radical extension of the original convenient SU(3) eightfold way hadron categorisation scheme.
Experiments in scattering very high energy electrons off neutrons and protons first showed evidence that each nucleon had a more complex structure than a simple point in the 1950s, and therefore the idea that these nucleons were simply fundamental particles was undermined. Another problem with nucleons being fundamental particles was that of the magnetic moments of neutrons and protons. Dirac in 1929 initially claimed that the antiparticle his equation predicted for the electron was the already-known proton (the neutron was still undiscovered until 1932), but because he couldn’t explain why the proton is more massive than the electron, he eventually gave up on this idea and predicted the unobserved positron instead (just before it was discovered). The problem with the proton being a fundamental particle was that, by analogy to the positron, it would have a magnetic moment of 1 nuclear magneton, whereas in fact the measured value is 2.79 nuclear magnetons. Also, for the neutron, you would expect zero magnetic moment for a neutral spinning particle, but the neutron was found to have a magnetic moment of -1.91 nuclear magnetons. These figures are inconsistent with neutrons being fundamental particles, but are consistent with quark structure:
‘The fact that the proton and neutron are made of charged particles going around inside them gives a clue as to why the proton has a magnetic moment higher than 1, and why the supposedly neutral neutron has a magnetic moment at all.’ – Richard P. Feynman, QED, Penguin, London, 1990, p. 134.
To explain hadron physics, Zweig and Gell-Mann suggested the theory that baryons are composed of three quarks. But there was immediately the problem the Omega Minus would contain three identical strange quarks, violating the Pauli exclusion principle that prevents particles from occupying the same set of quantum numbers or states. (Pairs of otherwise identical electrons in an orbital have opposite spins, giving them different sets of quantum numbers, but because there are only two spin states, you can’t make three identical charges share the same orbital by having different spins. Looking at the measured 3/2-spin of the Omega Minus, all of its 1/2-spin strange quarks would have the same spin.) To get around this problem in the experimentally discovered Omega Minus, the quarks must have an additional quantum number, due to the existence of a new charge, namely the colour charge of the strong force that comes in three types (red, blue and green). The SU(3) symmetry of colour force gives rise to (3*3)-1 = 8 gauge bosons, called gluons. Each gluon is a charged combination of a colour and the anticolour of a different colour, e.g. a gluon might be charged blue-antigreen. Because gluons carry a charge, unlike photons, they interact with one another and also with with virtual quarks produced by pair production due to the intense electromagnetic fields near fermions. This makes the strong force vary with distance in a different way to that of the electromagnetic force. At small distances from a quark, the net colour charge increases in strength with increasing distance, which the opposite of the behaviour of the electromagnetic charge (which gets bigger at smaller distances, due to less intervening shielding by the polarized virtual fermions caused in pair production). The overall result is that quarks confined in hadrons have asymptotic freedom to move about over a certain range of distances, which gives nucleons their size. Before the quark theory and colour charge had been discovered, Yukawa discovered a theory of strong force attraction that predicted the strong force was due to pion exchange. He predicted the mass of the pion, although unfortunately the muon was discovered before the pion, and was originally inaccurately identified as Yukawa’s exchange radiation. Virtual pions and other virtual mesons are now understood to mediate the strong interaction between nucleons as a relatively long-range residue of the colour force.

Above: the electroweak charges of the Standard Model of mainstream particle physics. The argument we made is that U(1) symmetry isn’t real and must be replaced by SU(2) with two charges and massless versions of the weak boson triplet (we do this by replacing the Higgs mechanism with a simpler mass-giving field that gives predictions of particle masses). The two charged gauge bosons simply mediate the positive and negative electric fields of charges, instead of having neutral photon gauge bosons with 4 polarizations. The neutral gauge boson of the massless SU(2) symmetry is the graviton. The lepton singlet with right handed spin in the standard model table above is not really a singlet: because SU(2) is now being used for electromagnetism rather than U(1), we have automatically a theory that unites quarks and leptons. The problem of the preponderance of matter over antimatter is also resolved this way: the universe is mainly hydrogen, one electron, two quarks and one downquark. The electrons are not actually produced alone. The downquark, as we will demonstrate below, is closely related to the electron.
The fractional charge is due to vacuum polarization shielding, with the accompanying conversion of electromagnetic field energy into short-ranged virtual particle mediated nuclear fields. This is a predictive theory even at low energy because it can make predictions based on conservation of field quanta energy where vacuum polarization attenuates a field, and the conversion of leptons into quarks requires higher energy than existing experiments have had access to. So electrons are not singlets: some of them ended up being converted into quarks in the big bang in very high energy interactions. The antimatter counterpart for the electrons in the universe is not absent but is present in nuclei, because those positrons were converted into the upquarks in hadrons. The handedness of the weak force relates to the fact that in the early stages of the big bang, for each two electron-positron pairs that were produced by pair production in the intense, early vacuum fields of the universe, both positrons but only one electron were confined to produce a proton. Hence the amount of matter and antimatter in the universe is identical, but due to reactions related to the handedness of the weak force, all the anti-positrons were converted into upquarks, but only half of the electrons were converted into downquarks. We’re oversimplifying a little because some neutrons were produced, and quite a few other minor interactions occurred, but this is approximately the overall result of the reactions. The Standard Model table of particles above is in error because it assumes that leptons and quarks are totally distinct. For a more fundamental level of understanding, we need to alter the electroweak portion of the Standard Model.
The apparent deficit of antimatter in the universe is simply a miss-observation: the antimatter has simply been transformed from leptons into quarks, which from a long distance display different properties and interactions to leptons (due to cloaking by the polarized vacuum and to close confinement causing colour charge to physically appear by inducing asymmetry; the colour charge of a lepton is invisible because it is symmetrically distributed over three preons in a lepton, and cancels out to white unless an enormous field strength due to the extremely close proximity of another particle is present, creating an asymmetry in the preon arrangement is produced, allowing a net colour charge to operate on the other nearby particle), so it isn’t currently being acknowledged for what it really is. (Previous discussions of the relationship of quarks to leptons on this blog include https://nige.wordpress.com/2007/06/13/feynman-diagrams-in-loop-quantum-gravity-path-integrals-and-the-relationship-of-leptons-to-quarks/ and https://nige.wordpress.com/2007/07/17/energy-conservation-in-the-standard-model/ where suggestions by Carl Brannen and Tony Smith are covered.)
Considering the strange quarks in the Omega Minus, which contains three quarks each of electric charge -1/3, vacuum polarization of three nearby leptons would reduce the -1 unit observable charge per lepton to -1/3 observable charge per lepton, because the vacuum polarization in quantum field theory which shields the core of a particle occurs out to about a femtometre or so, and this zone will overlap for three quarks in a baryon like the Omega Minus. The overlapping of the polarization zone will make it three times more effective at shielding the core charges than in the case of a single charge like a single electron. So the electron’s observable electric charge (seen from a great distance) is reduced by a factor of three to the charge of a strange quark or a downquark. Think of it by analogy a couple sharing blankets which act as shields, reducing the emission of thermal radiation. If each of the couple contribute one blanket, then the overlap of blankets will double the heat shielding. This is basically what happens when N electrons are brought close together so that they share a common (combined) vacuum polarization shell around the core charges: the shielding gives each charge in the core an apparent charge (seen from outside the vacuum polarization, i.e., more than a few femtometres away) of 1/N charge units. In the case of upquarks with apparent charges of +2/3, the mechanism is more complex, since the -1/3 charges in triplets are the clearest example of the mechanism whereby shared vacuum polarization shielding transforms properties of leptons into those of quarks. The emergence of colour charge when leptons are confined together also appears to have a testable, falsifiable mechanism because we know how much energy becomes available for the colour charge as the observable electric charge falls (conservation of energy suggests that the attenuated electromagnetic charge gets converted into colour charge energy). For the mechanism of the emergence of colour charge in quarks from leptons, see the suggestions of Tony Smith and Carl Brannen, outlined at https://nige.wordpress.com/2007/07/17/energy-conservation-in-the-standard-model/.
In particularly, the Cabibbo mixing angle in quantum field theory indicates a strong universality in reaction rates for leptons and quarks: the strength of the weak force when acting on quarks in a given generation is similar to that for leptons to within 1 part in 25. The small 4% difference in reaction rates arises, as explained by Cabibbo in 1964, due to the fact that a lepton has only one way to decay, but a quark has two decay routes, with probabilities of 96% and 4% respectively. The similarity between leptons and quarks in terms of their interactions is strong evidence that they are different manifestations of common underlying preons, or building blocks.

Above: Coulomb force mechanism for electrically charged massless gauge bosons. The SU(2) electrogravity mechanism. Spin-1 gauge bosons for fundamental interactions: the massive versions of the SU(2) Yang-Mills gauge bosons are the weak field quanta which only interact with left-handed particles. One half (corresponding to exactly one handedness for weak interactions) of SU(2) gauge bosons acquire mass at low energy; the other half are the gauge bosons of electromagnetism and gravity.
Think of two flak-jacket protected soldiers firing submachine guns towards one another, while from a great distance other soldiers (who are receding from the conflict) fire bullets in at both of them. They will repel because of net outward force on them, due to successive impulses both from bullet strikes received on the sides facing one another, and from recoil as they fire bullets. The bullets hitting their backs have relatively smaller impulses since they are coming from large distances and so due to drag effects their force will be nearly spent upon arrival (analogous to the redshift of radiation emitted towards us by the bulk of the receding matter, at great distances, in our universe). That explains the electromagnetic repulsion physically. Now think of the two soldiers as comrades surrounded by a mass of armed savages, approaching from all sides. The soldiers stand back to back, shielding one another’s back, and fire their submachine guns outward at the crowd. In this situation, they attract, because of a net inward acceleration on them, pushing their backs toward towards one another, both due to the recoils of the bullets they fire, and from the strikes each receives from bullets fired in at them. When you add up the arrows in this diagram, you find that attractive forces between dissimilar unit charges have equal magnitude to repulsive forces between similar unit charges. This theory holds water!
This predicts the right strength of gravity, because the charged gauge bosons will cause the effective potential of those fields in radiation exchanges between similar charges throughout the universe (drunkard’s walk statistics) to multiply up the average potential between two charges by a factor equal to the square root of the number of charges in the universe. This is so because any straight line summation will on average encounter similar numbers of positive and negative charges as they are randomly distributed, so such a linear summation of the charges that gauge bosons are exchanged between cancels out. However, if the paths of gauge bosons exchanged between similar charges are considered, you do get a net summation.

Above: Charged gauge bosons mechanism and how the potential adds up, predicting the relatively intense strength (large coupling constant) for electromagnetism relative to gravity according to the path-integral Yang-Mills formulation. For gravity, the gravitons (like photons) are uncharged, so there is no adding up possible. But for electromagnetism, the attractive and repulsive forces are explained by charged gauge bosons. Notice that massless charge electromagnetic radiation (i.e., charged particles going at light velocity) is forbidden in electromagnetic theory (on account of the infinite amount of self-inductance created by the uncancelled magnetic field of such radiation!) only if the radiation is going solely in only one direction, and this is not the case obviously for Yang-Mills exchange radiation, where the radiant power of the exchange radiation from charge A to charge B is the same as that from charge B to charge A (in situations of equilibrium, which quickly establish themselves). Where you have radiation going in opposite directions at the same time, the handedness of the curl of the magnetic field is such that it cancels the magnetic fields completely, preventing the self-inductance issue. Therefore, although you can never radiate a charged massless radiation beam in one direction, such beams do radiate in two directions while overlapping. This is of course what happens with the simple capacitor consisting of conductors with a vacuum dielectric: electricity enters as electromagnetic energy at light velocity and never slows down. When the charging stops, the trapped energy in the capacitor travels in all directions, in equilibrium, so magnetic fields cancel and can’t be observed. This is proved by discharging such a capacitor and measuring the output pulse with a sampling oscilloscope.
The price of the random walk statistics needed to describe such a zig-zag summation (avoiding opposite charges!) is that the net force is not approximately 1080 times the force of gravity between a single pair of charges (as it would be if you simply add up all the charges in a coherent way, like a line of aligned charged capacitors, with linearly increasing electric potential along the line), but is the square root of that multiplication factor on account of the zig-zag inefficiency of the sum, i.e., about 1040 times gravity. Hence, the fact that equal numbers of positive and negative charges are randomly distributed throughout the universe makes electromagnetism strength only 1040/1080 = 10-40 as strong as it would be if all the charges were aligned in a row like a row of charged capacitors (or batteries) in series circuit. Since there are around 1080 randomly distributed charges, electromagnetism as multiplied up by the fact that charged massless gauge bosons are Yang-Mills radiation being exchanged between all charges (including all charges of similar sign) is 1040 times gravity. You could picture this summation by the physical analogy of a lot of charged capacitor plates in space, with the vacuum as the dielectric between the plates. If the capacitor plates come with two opposite charges and are all over the place at random, the average addition of potential works out as that between one pair of charged plates multiplied by the square root of the total number of pairs of plates. This is because of the geometry of the addition. Intuitively, you may incorrectly think that the sum must be zero because on average it will cancel out. However, it isn’t, and is like the diffusive drunkard’s walk where the average distance travelled is equal to the average length of a step multiplied by the square root of the number of steps. If you average a large number of different random walks, because they will all have random net directions, the vector sum is indeed zero. But for individual drunkard’s walks, there is the factual solution that a net displacement does occur. This is the basis for diffusion. On average, gauge bosons spend as much time moving away from us as towards us while being exchanged between the charges of the universe, so the average effect of divergence is exactly cancelled by the average convergence, simplifying the calculation. This model also explains why electromagnetism is attractive between dissimilar charges and repulsive between similar charges.
We are pushed down to Earth because the Earth shields us from gravitons in the downward direction, creating a small amount of asymmetry in the exchange of gravitons between us and the surrounding universe (the cross-section for graviton shielding by an electron is only its black hole event horizon cross-sectional area, i.e. 5.75*10-114 square metres). The special quasi-compressive effects of gravitons on masses accounts for the ‘curvature’ effects of general relativity, such as the fact that the Earth’s radius is 1.5 mm less than the figure given by Euclidean geometry (Feynman Lectures on Physics, c42 p6, equation 42.3).
As soon as you do include masses in the surrounding universe (which are far bigger even though they are further away, i.e., the mass of the Earth and an apple is only 1 part in 1029 of the mass of the universe, and all masses are gravitational charges which exchange gravitons with all other masses and with energy!), you begin to see what is really occurring. Spin-1 gauge bosons are gravitons!
Cosmologically distant masses push one another apart by exchanging gravitons, explaining the lack of gravitational deceleration observed in the universe. But masses which are nearby in cosmological terms (not redshifted much relative to one another) are pushed together by gravitons from the surrounding (highly redshifted) distant universe, because they don’t exert an outward force relative to one another, and so don’t fire a recoil force (mediated by spin-1 gravitons) towards one another. They, in other words, shield each other. Think of the exchange simply as bullets bouncing off particles. If bullets are firing in from all directions, the proximity of a nearby mass which isn’t shooting at you will act as a shield, and you’d be pushed towards that shield (which is why things fall towards large masses). This is a quantitative prediction, predicting the strength of the gravitational coupling which can be checked. So this mechanism, which predicted the lack of gravitational deceleration in the big bang in 1996 (observed in 1998 by Saul Perlmutter’s automated CCD telescope software) ,also predicts gravitation, quantitatively.
It should be noted that in this diagram we have drawn the force-causing gauge or vector boson exchange radiation in the usual convention as a horizontal wavy line (i.e., the gauge bosons are shown as being instantly exchanged, not as radiation propagating at the velocity of light and thus taking time to propagate). In fact, gauge bosons don’t propagate instantly and to be strictly accurate we would need to draw inclined wavy lines. The exchange of the gauge bosons as a kind of reflection process (which imparts an impulse in the case where it causes the mass to accelerate) would make the diagram more complex. Conventionally, Feynman diagrams are shorthand for categories of interactions, not for specific individual interactions. Therefore, they are not depicting all the similar interactions that occur when two particles attract or repel; they are way oversimplified in order to make the basic concept lucid.
Loops in Feynman diagrams and the associated infinite perturbative expansion
Because the gravitational phenomena we have observed manifested in checked aspects of general relativity are at low energy, phenomena such as loops (whereby bosonic field quanta undergo pair production and briefly become fermionic pairs which soon annihilate back into bosons, but become briefly polarized during their existence and in so doing modify the field) which are described by the infinite series of Feynman diagrams each representing one term in the infinite series of terms in the perturbative expansion to a Feynman path integral, can be ignored (this is discussed later in this post). So the direct exchange of gauge bosons such as gravitons, gives us only a few possible types of Feynman diagrams for non-loop, simple, direct exchange of field quanta between charges. These are called ‘tree diagrams’. Important results include:
1. Quantization of mass: the force of gravity is proportional not to M1M2 but instead to M2, which is a vital result because this is evidence for the quantization of mass. We are dealing with unit masses, fundamental particles. Lepton and hadron masses beyond the electron are nearly all integer denominations of 0.5*0.511*137 = 35 MeV where 0.511 MeV is the electron’s mass and 137.036… is the well known Feynman dimensioness factor in charge renormalization (discovered much earlier in quantum mechanics by Sommerfeld); furthermore, quark doublet or meson masses are close to multiples of twice this or 70 MeV while quark triplet or baryon masses are close to multiples of three times this or 105 MeV; it appears that the simplest possible model, which predicts masses of new as yet unobserved particles as well as explaining existing particle masses, is that the vacuum particle which is the building block of mass is 91 GeV like the Z weak boson; the muon mass for instance is 91,000 divided by the product of 137 and twice Pi, which is a combination of a 137 vacuum polarization shielding factor, and twice Pi which is a dimensionless geometric shield factor, e.g. spinning a particle or a missile in flight reduces the radiant exposure per unit area of its spinning surface by Pi as compared to a non-spinning particle or missile, because the entire surface area of the edge of a loop or cylinder is Pi times the cross-sectional area seen side-on, while a spin-1/2 fermion must rotate twice, i.e., by 720 not 360 degrees – like drawing a line right around the single-surface of the Möbius strip – to expose its entire surface to observation and reset its symmetry. This is analysed in an earlier blog post, showing how all masses are built up from only one type of fundamental massive particle in the vacuum, and making checkable predictions. Polarized vacuum veils around particles reduce the strength of the coupling between the massive 91 GeV vacuum particles (which interact with gravitons) and the SU(2) x SU(3) particle core of interest (which doesn’t directly interact with gravitons), accounting for the observed discrete spectrum of fundamental particle masses.
The correct mass giving field is different in some ways to the electroweak symmetry breaking Higgs field of the conventional Standard Model (which gives the standard model charges as well as the 3 weak gauge bosons their symmetry-breaking mass at low energies by ‘miring’ them or resisting their acceleration): a discrete number of the vacuum mass particles (gravitational charges) become associated with leptons and hadrons, either within the vacuum polarized region which surrounds them (strong coupling to the massive particles, hence large effective masses) or outside it (where the coupling, which presumably relies on the electromagnetic interaction, is shielded and weaker, giving lower effective masses to particles). In the case of the deflection of light by gravity, the photons have zero rest mass so it is their energy content which is causing deflection. The mass-giving field in the vacuum still mediates effects of gravitons, but the photon has no net electric charge (it has equal amounts of positive and negative electric field density), it has zero effective rest mass. The quantum mechanism by which light gets deflected as predicted by general relativity has been analysed in an earlier post: due to the FitzGerald-Lorentz contraction, a photon’s field lines are all in a plane perpendicular to the direction of propagation. This means that twice the electric field’s energy density in a photon (or other light velocity particle) is parallel to a gravitational field line that the photon is crossing at normal incidence, compared to the case for a slow-moving charge with an isotropic electric field. The strength of the coupling between the photon’s electric field and the mass-giving particles in the vacuum is generally not quantized, unless the energy of the photon is quantized.
If you are firmly attached to an accelerating horse, you will accelerate at the specific rate that the horse accelerates at. But if you are less firmly attached, the acceleration you get depends on your adhesion to the saddle. If you slide back as the horse accelerates, your acceleration is somewhat less than that of the horse you are sitting on. Particles with rest mass are firmly anchored to vacuum gravitational charges, the particles with fixed mass that replace the traditional role of Higgs bosons. But particles like photons, which lack rest mass, are not firmly attached to the massive vacuum field, and the quantized gravitational interactions – like a fixed acceleration of a horse – is not automatically conveyed upon the photon. The result is that a photon gets deflected more classically by ‘curved spacetime’ created by the effect of gravitons upon the Higgs-like massive bosons in the vacuum, than particles with rest mass such as electrons.
2. The inverse square law, for distance r.
3. Many checked and checkable quantitative predictions. Because the Hubble constant and the density of the universe can be quantitatively measured (within certain error bars, like all measurements), you can use this to predict the value of G. As astronomy gets better measurements, the accuracy of the prediction gets better and can be checked experimentally.
In addition, the mechanism predicts the expansion of the universe: the reason why Yang-Mills exchange radiation is redshifted to lower energy by bouncing off distant masses is that energy from gravitons is being used to cause the distant masses to speed up. This makes quantitative predictions, and is a firm test of the theory. (The outward force of a receding galaxy of mass m is F = mH2R, which requires power P = dE/dt = Fv = mH3R2, where E is energy.)
It should be noted that the gravitons in this model would have a mean free path (average distance between interactions) of 3.10 x 10^77 metres in water, as calculated in the earlier post here. These are able to produce gravity by interacting with the the Higgs-like vacuum field, due to the tremendous flux of gravitons involved. The radially symmetric, isotropic outward force of the receding universe is on the order 10^43 Newtons, and by Newton’s 3rd law this produces a similar equal and opposite (inward) reaction force. This is the immense field behind gravitation. Only a trivial asymmetry in the normal equilibrium of such immense forces is enough to produce gravity. Cosmologically nearby masses are pushed together because they aren’t receding much, and so don’t exert a forceful flux of graviton exchange radiation in the direction of other (cosmologically) nearby masses. Because (cosmologically) nearby masses therefore don’t exert graviton forces upon each other as exchange radiation, they are shielding one another in effect, and therefore get pushed together by the forceful exchange of gravitons which does occur with the receding universe on the unshielded side, as illustrated in Fig. 1 above.
Dr Thomas Love of California State University has pointed out:
‘The quantum collapse [in the mainstream interpretation of of quantum mechanics, which has wavefunction collapse occur when a measurement is made] occurs when we model the wave moving according to Schroedinger (time-dependent) and then, suddenly at the time of interaction we require it to be in an eigenstate and hence to also be a solution of Schroedinger (time-independent). The collapse of the wave function is due to a discontinuity in the equations used to model the physics, it is not inherent in the physics.’
That looks like a factual problem, undermining the mainstream interpretation of the mathematics of quantum mechanics. If you think about it, sound waves are composed of air molecules, so you can easily write down the wave equation for sound and then – when trying to interpret it for individual air molecules – come up with the idea of wavefunction collapse occurring when a measurement is made for an individual air molecule.
Feynman writes on a footnote printed on pages 55-6 of my (Penguin, 1990) copy of his book QED:
‘… I would like to put the uncertainty principle in its historical place: when the revolutionary ideas of quantum physics were first coming out, people still tried to understand them in terms of old-fashioned ideas … But at a certain point the old-fashioned ideas would begin to fail, so a warning was developed … If you get rid of all the old-fashioned ideas and instead use the [path integral] ideas that I’m explaining in these lectures – adding arrows for all the ways an event can happen – there is no need for an uncertainty principle!’
Feynman on p85 points out that the effects usually attributed to the ‘uncertainty principle’ are actually due to interferences from virtual particles or field quanta in the vacuum (which don’t exist in classical theories but must exist in an accurate quantum field theory):
‘But when the space through which a photon moves becomes too small (such as the tiny holes in the screen), these [classical] rules fail – we discover that light doesn’t have to go in straight lines, there are interferences created by two holes … The same situation exists with electrons: when seen on a large scale, they travel like particles, on definite paths. But on a small scale, such as inside an atom, the space is so small that there is no main path, no ‘orbit’; there are all sorts of ways the electron could go, each with an amplitude. The phenomenon of intereference becomes very important, and we have to sum the arrows to predict where an electron is likely to be.’
Hence, in the path integral picture of quantum mechanics – according to Feynman – all the indeterminancy is due to interferences. It’s very analogous to the indeterminancy of the motion of a small grain of pollen (less than 5 microns in diameter) due to jostling by individual interactions with air molecules, which represent the field quanta being exchanged with a fundamental particle.
The path integral then makes a lot of sense, as it is the statistical resultant for a lot of interactions, just as the path integral was actually used for brownian motion (diffusion) studies in physics before its role in QFT. The path integral still has the problem that it’s unrealistic in using calculus and averaging an infinite number of possible paths determined by the continuously variable lagrangian equation of motion in a field, when in reality there are not going to be an infinite number of interactions taking place. But at least, it is possible to see the problems, and entanglement may be a red-herring:
‘It always bothers me that, according to the laws as we understand them today, it takes a computing machine an infinite number of logical operations to figure out what goes on in no matter how tiny a region of space, and no matter how tiny a region of time. How can all that be going on in that tiny space? Why should it take an infinite amount of logic to figure out what one tiny piece of spacetime is going to do? So I have often made the hypothesis that ultimately physics will not require a mathematical statement, that in the end the machinery will be revealed, and the laws will turn out to be simple, like the chequer board with all its apparent complexities.’
– R. P. Feynman, The Character of Physical Law, BBC Books, 1965, pp. 57-8.
copy of a comment:
http://asymptotia.com/2008/02/17/tales-from-the-industry-xvii-jump-thoughts/
Hi Clifford,
Thanks for these further thoughts about being science advisor […] for what is (at least partly) a sci fi film. It’s fascinating.
“What I like to see first and foremost in these things is not a strict adherence to all known scientific principles, but instead internal consistency.”
Please don’t be too hard on them if there are apparent internal inconsistencies. Such alleged internal inconsistencies don’t always matter, as Feynman discovered:
“… take the exclusion principle … it turns out that you don’t have to pay much attention to that in the intermediate states in the perturbation theory. I had discovered from empirical rules that if you don’t pay attention to it, you get the right answers anyway …. Teller said: “… It is fundamentally wrong that you don’t have to take the exclusion principle into account.” …
“… Dirac asked “Is it unitary?” … Dirac had proved … that in quantum mechanics, since you progress only forward in time, you have to have a unitary operator. But there is no unitary way of dealing with a single electron. Dirac could not think of going forwards and backwards … in time …
” … Bohr … said: “… one could not talk about the trajectory of an electron in the atom, because it was something not observable.” … Bohr thought that I didn’t know the uncertainty principle …” – Feynman, quoted at http://www.tony5m17h.net/goodnewsbadnews.html#badnews
I agree with you that: “Entertainment leading to curiosity, real questions, and then a bit of education …”
“… Smolin has launched a controversial attack on those working on the dominant model in theoretical physics. He accuses string theorists of racism, sexism, arrogance, ignorance, messianism and, worst of all, of wasting their time on a theory that hasn’t delivered.”
–
http://tls.timesonline.co.uk/article/0,,25372-2650590_1,00.html
‘rock guitars could hold secret to the universe’. It might sound like just more pathetic spin, but actually, the analogy of string theory hype to that of a community of rock groupies is sound.
The rock guitar string promoter referred to just above is Dr Lewney who has the site http://www.doctorlewney.com/. He writes on Dr Woit’s blog:
‘I’m actually very open to ideas as to how best to communicate physics to schoolkids.’
Dr Lewney, if you want to communicate real, actual physics rather than useless blathering and lies to schoolkids, that’s really excellent. But please just remember that physics is not uncheckable speculation, and that twenty years of mainstream hype of string theory in British TV, newspapers and the New Scientist has by freak ‘coincidence’ (don’t you believe it) correlated with a massive decline in kids wanting to do physics. Maybe they’re tired of sci fi dressed up as physics or something.
http://www.buckingham.ac.uk/news/newsarchive2006/ceer-physics-2.html:
‘Since 1982 A-level physics entries have halved. Only just over 3.8 per cent of 16-year-olds took A-level physics in 2004 compared with about 6 per cent in 1990.
‘More than a quarter (from 57 to 42) of universities with significant numbers of physics undergraduates have stopped teaching the subject since 1994, while the number of home students on first-degree physics courses has decreased by more than 28 per cent. Even in the 26 elite universities with the highest ratings for research the trend in student numbers has been downwards.
‘Fewer graduates in physics than in the other sciences are training to be teachers, and a fifth of those are training to be maths teachers. A-level entries have fallen most sharply in FE colleges where 40 per cent of the feeder schools lack anyone who has studied physics to any level at university.’
http://www.math.columbia.edu/~woit/wordpress/?p=651#comment-34820:
‘One thing that is clear is that hype of speculative uncheckable string theory has at least failed to encourage a rise in student numbers over the last two decades, assuming that such speculation itself is not actually to blame for the decline in student interest.
‘However, it’s clear that when hype fails to increase student interest, everyone will agree to the consensus that the problem is a lack of hype, and if only more hype of speculation was done, the problem would be addressed.’
Professor John Conway, a physicist at the University of California, has written a post called ‘What’s the (Dark) Matter?’ where someone has referred to my post here as my ‘belief’ that gravitons are of spin-1. Actually, this isn’t a ‘belief’. It’s a fact (not a belief) that so far, spin-2 graviton ideas are at best uncheckable speculation that is ‘not even wrong‘, and it’s a fact (not a belief) that this post shows that spin-1 gravitons do reproduce gravitation as already known from the checked and confirmed results of general relativity, plus quantitatively predicting more stuff such as the strength of gravity. This is not a mere ‘personal belief’, such as the gut feeling that is used by string theorists, politicians and priests to justify hype in religion or politics. It is instead fact-based, not belief-based, and it makes accurate predictions so far as the difficult
Because the effective value of G at early times after the big bang is so small from our spacetime perspective, we see small gravitational effects: the universe looks very flat, i.e., gravity was so weak it was unable to clump matter very much at 400,000 years after the big bang, which is the time of our information on flatness, i.e. the time that the closely studied cosmic background radiation was emitted. The mainstream ad hoc explanation for this kind of observation is a non-falsifiable (endlessly adjustable) idea from Alan Guth that the universe expanded or ‘inflated’ at a speed faster than light for a small fraction of a second, which would have allowed the limited total mass to get very far dispersed very quickly, which would have reduced the curvature of the universe and suppressed the effects of gravitation at subsequent times in the early universe.
On the topic of variations in G, Edward Teller falsely claimed in a 1948 paper that if G had varied as Dirac suggested a few years earlier, then the gravitationally caused compression in the early universe and in stars including the sun would vary with time, affecting fusion rates dramatically because fusion is highly sensitive to the amount of compression (which he knew from his Los Alamos studies on the difficulty of producing a hydrogen bomb at that time). However, the Yang-Mills mechanism of electromagnetism (whose role in fusion is the Coulomb repulsion of protons, i.e., the stronger electromagnetism is, the less fusion you get because protons approach less closely because they are repelled more strongly, so the short-ranged strong force which causes protons to fuse together ends up causing less fusion), shows that it will vary with time in the same way that gravitation does.
This invalidates Teller’s theory, because if you for example halve the value of G (making fusion more difficult by reducing the compression of protons long ago), you simultaneously get an electromagnetic coupling charge which is halved, and the effect of the latter is to increase fusion by reducing the Coulomb barrier which protons need to overcome in order to fuse. The two effects – reduced G which tends to reduce fusion by reducing compression, and reduced Coulomb charge which allows protons to approach closer before being repelled, and therefore increases fusion – offset one another. Dirac wrongly suggested that G falls with time, because he believed that at early times G was as strong as electromagnetism and numerically ‘unified’; actually all attempts to explain the universe by claiming that the fundamental forces including gravity are the same at a particular very early time/high energy, are physically flawed and violate the conservation of energy – the whole reason why the strong force charge strength falls at higher energies is because it is being caused by pair-production of virtual particles including virtual quarks accompanied by virtual gluons. This pair-production is a result of the electromagnetic charge, which increases at higher energy.
‘A Party member … is supposed to live in a continuous frenzy of hatred of foreign enemies and internal traitors … The discontents produced by his bare, unsatisfying life are deliberately turned outwards and dissipated by such devices as the Two Minutes Hate, and the speculations which might possibly induce a skeptical or rebellious attitude are killed in advance by his early acquired inner discipline … called, in Newspeak, crimestop. Crimestop means the faculty of stopping short, as though by instinct, at the threshold of any dangerous thought. It includes the power of not grasping analogies, of failing to perceive logical errors, of misunderstanding the simplest arguments if they are inimical to Ingsoc, and of being bored or repelled by any train of thought which is capable of leading in a heretical direction. Crimestop, in short, means protective stupidity.’ – Orwell, 1984.
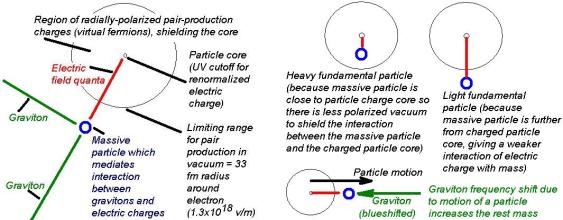
Above: Simplified depiction of the coupling scheme for mass to be given to Standard Model particles by a separate field, which is the man-in-the-middle between graviton interactions and electromagnetic interactions. A more detailed analysis of the model, with a couple of mathematical variations and some predictions of masses for different leptons and hadrons, is given in the earlier post here and there are updates in other recent posts on this blog. In the case of quarks, the cores are so close together that they share the same ‘veil’ of polarized vacuum, so N quarks in close proximity (asymptotic freedom inside hadrons) boosts its electric charge shielding factor by a factor N, so if you have three quarks of bare charge –j each and normal vacuum polarization shielding factor j, the total charge is not –jN but is –jN/N, where the N in the denominator is there to account for the increased vacuum shielding. Obviously –jN/N = -j, so 3 electron-charge quarks in close proximity will only exhibit the combined charge of 1 electron, as seen at a distance beyond 33 fm from the core. Hence, in such a case, the apparent electric charge contribution per quark is only -1/N = -1/3, which is the exactly what happens in the Omega Minus particle (which has 3 strange quarks of apparent charge -1/3 each, giving the Omega Minus a total apparent electric charge as observed beyond 33 fm of -1 unit). More impressively, this model predicts the masses of all leptons and hadrons, and also makes falsifiable predictions about the variation in coupling constants as a function of energy which result from the conversion of electromagnetic field energy into short range nuclear force field quanta as a result of pair-production of particles including weak gauge bosons, virtual quarks and gluons in the electromagnetic field at high energy (short distances from the particle core). The energy lost from the electromagnetic field, due to vacuum polarization opposing the electric charge core, gets converted into short range nuclear force fields. From the example of the Omega Minus particle, we can see that the electric charge per quark observable at long ranges is reduced from -1 to -1/3 unit due to the close proximity of three similarly charge quarks, as compared to a single particle core surrounded by polarized vacuum, i.e. a lepton (the Omega Minus is a unique, very simple situation; usually things are far and away more complicated because hadrons generally contain pairs or triplets of quarks of different flavour). Hence, 2/3rds of the electric field energy that occurs when only one particle is alone in a polarized vacuum (i.e. a lepton) is used to generate short-ranged weak and strong nuclear force fields when three such particles are closely confined.
As discussed in earlier posts, the similarity of leptons and quarks has been known since 1964, when it was discovered by the Italian physicist Nicola Cabibbo: the rates of lepton interactions are identical to those of quarks to within just 4%, or one part in 25. The weak force when acting on quarks within one generation of quarks is identical to within 1 part in 25 of that when acting on leptons (although if the interaction is between two quarks of different generations, the interaction is weaker by a factor of 25). This similarity of quarks and leptons is called ‘universality’. Cabibbo brilliantly suggested that the slight (4%) difference between the action of the weak force on leptons and quarks is due to the fact that a lepton has only one way to decay, whereas a quark has two possible decay routes, with relative probabilities of 1/25 and 24/45, the sum being of course (1/25) + (24/25) = 1 (the same as that for a lepton). But because only the one quark decay route or the other (1/25 or 24/25) is seen in an experiment, the effective rate of quark interactions are lower than those for leptons. If the weak force involves an interaction between just one generation of quarks, it is 24/25 or 96% as strong as between leptons, but if it involves two generations of quarks, it is only 1/25th as strong as when mediating a similar interaction for leptons.
This is very strong evidence that quarks and leptons are fundamentally the same thing, just in a different disguise due to the way they are paired or tripleted and ’dressed’ by the surrounding vacuum polarization (electric charge shielding effects, and the use of energy to mediate short-range nuclear forces).
A quick but vital update about my research (particularly updating the confusion in some of the comments to this blog post): I’ve obtained the physical understanding which was missing from the QFT textbooks I’ve been studying by Weinberg, Ryder and Zee, from the 2007 edition of Professor Frank Close’s nicely written little book The Cosmic Onion, Chapter 8, ‘The Electroweak Force’.
Close writes that the field quanta of U(1) in the standard model is not the photon, but is a B0 field quanta.
SU(2) gives rise to field quanta W+, W– and W0. The photon and the Z0 both result from the Weinberg ‘mixing’ of the electrically neutral W0 from SU(2) with the electrically neutral B0 from U(1).
This is precisely the information I was looking for, which was not clearly stated in the QFT textbooks. It enables me to get a physical feel for how the mathematics works.
The Weinberg mixing angle determines how W0 from SU(2) and B0 from U(1) mix together to yield the photon (textbook electromagnetic field quanta) and the Z0 massive neutral weak gauge boson.
If the Weinberg mixing angle were zero, then W0 = Z0 and B0 = electromagnetic photon. However, this simple scheme fails (although this failure is not made clear in any of the QFT textbooks I’ve read, which have obfuscated instead), and an ad hoc or fudged mixing angle of about 26 degrees (this is the angle between the Z0 and W0 phase vectors) is required.
Here’s a brief comment about the vague concept of a ‘zero point field’ which unhelpfully ignores the differences between fundamental forces and mixes up gravitational and electromagnetic field quanta interactions to create a muddle. Traditional calculations of that ‘field’ (there isn’t only one field acting on ground state for electrons; there is gravity and electromagnetism with different field quanta needed to explain why one is always attractive and the other is attractive only between unlike charges and repulsive between similar charges, not to mention explaining the 10^40 difference in field strengths for those forces) give a massive energy density to the vacuum, far higher than that observed with respect to the small positive cosmological constant in general relativity. However, two separate force fields are there being confused. The estimates of the ‘zero point field’ which are derived from electromagnetic phenomena such as electrons in the ground state of hydrogen being in an equilibrium of emission and reception of field quanta, have nothing to do with the graviton exchange that causes the cosmic expansion (Figure 1 above has the mechanism for that). There is some material about traditional ‘zero point field’ philosophy on Wikipedia
The radius of the event horizon of a black hole electron is on the 1.4*10^{-57} m, the equation being simply r = 2GM/c^2 where M is electron mass.
Compare this to Planck’s length 1.6 * 10^{−35} metres which is a dimensional analysis-based (non physical) length far larger in size, yet historically claimed to be the smallest physically significant size!
The black hole length equation is different from the Planck length equation principally in that Planck’s equation includes Planck’s constant h, and doesn’t include electron mass. Both equations contain c and G. The choice of which is the more fundamental equation should be based on physical criteria, not groupthink or the vagaries of historical precedence.
The Planck length is complete rubbish, it’s not based on physics, it’s unchecked physically, it’s not even wrong uncheckable speculation.
The smaller black hole size is checkable because it causes physical effects. According to the Wikipedia page: http://en.wikipedia.org/wiki/Black_hole_electron
“A paper titled “Is the electron a photon with toroidal topology?” by J. G. Williamson and M. B. van der Mark, describes an electron model consisting of a photon confined in a closed loop. In this paper, the confinement method is not explained. The Wheeler suggestion of gravitational collapse with conserved angular momentum and charge would explain the required confinement. With confinement explained, this model is consistent with many electron properties. This paper argues (page 20) “–that there exists a confined single-wavelength photon state, (that) leads to a model with non-trivial topology which allows a surprising number of the fundamental properties of the electron to be described within a single framework.” “
My papers in Electronics World, August 2002 and April 2003, similarly showed that an electron is physically identical to a confined charged photon trapped into a small loop by gravitation (i.e., a massless SU(2) charged gauge boson which has not been supplied by mass from the Higgs field; the detailed way that the magnetic field curls cancel when such energy goes round in a loop or alternatively is exchanged in both directions between charges, prevent the usual infinite-magnetic-self-inductance objection to the motion of charged massless radiations).
The Wiki page on black hole electrons then claims wrongly that:
All of these “objections” are based on flawed versions Hawking’s black hole radiation theory which neglects a lot of vital physics which make the correct theory more subtle.
See the Schwinger equation for pair production field strength requirements: equation 359 of the mainstream work http://arxiv.org/abs/quant-ph/0608140 for equation 8.20 of the mainstream work http://arxiv.org/abs/hep-th/0510040.
First of all, Schwinger showed that you can’t get spontaneous pair-production in the vacuum if the electromagnetic field strength is below the critical threshold of 1.3*10^18 volts/metre.
Hawking’s radiation theory requires this, because his explanation is that pair production must occur near the event horizon of the black hole.
One virtual fermion falls into the black hole, and the other escapes from the black hole and thus becomes a “real” particle (i.e., one that doesn’t get drawn to its antiparticle and annihilated into bosonic radiation after the brief Heisenberg uncertainty time).
In Hawking’s argument, the black hole is electrically uncharged, so this mechanism of randomly escaping fermions allows them to annihilate into real gamma rays outside the event horizon, and Hawking’s theory describes the emission spectrum of these gamma rays (they are described by a black body type radiation spectrum with a specific equivalent radiating temperature).
The problem is that, if the black hole does need pair production at the event horizon in order to produce gamma rays, this won’t happen the way Hawking suggests.
The electrical charge needed to produce Schwinger’s 1.3*10^18 v/m electric field which is the minimum needed to cause pair-production /annihilation loops in the vacuum, will modify Hawking’s mechanism.
Instead of virtual positrons and virtual electrons both having an equal chance of falling into the real core of the black hole electron, what will happen is that the pair will be on average polarized, with the virtual positron moving further towards the real electron core, and therefore being more likely to fall into it.
So, statistically you will get an excess of virtual positrons falling into an electron core and an excess of virtual electrons escaping from the black hole event horizon of the real electron core.
From a long distance, the sum of the charge distribution will make the electron appear to have the same charge as before, but the net negative charge will then come from the excess electrons around the event horizon.
Those electrons (produced by pair production) can’t annihilate into gamma rays, because not enough virtual positrons are escaping from the event horizon to enable them to annihilate.
This really changes Hawking’s theory when applied to fundamental particles as radiating black holes.
Black hole electrons radiate negatively charged massless radiation: gauge bosons. These are the Hawking radiation from black hole electrons. The electrons don’t evaporate to nothing, because they’re all evaporating and therefore all receiving radiation in equilibrium with emission.
This is part of the reason why SU(2) rather than U(1)xSU(2), looks to me like the best way to deal with electromagnetism as well as the weak and gravitational interaction! By simply getting rid of the Higgs mechanism and replacing it with something that provides mass to only a proportion of the SU(2) gauge bosons, we end up with massless charged SU(2) gauge bosons which mimic the charged, force-causing, Hawking radiation from black hole fermions. The massless neutral SU(2) gauge boson is then a spin-1 graviton, which fits in nicely with a quantum gravity mechanism that makes checkable predictions and is compatible with observed approximations such as checked parts of general relativity and quantum field theory.
********
Heaviside, Wolfgang Pauli, and Bell on the Lorentz spacetime
There are a couple of nice articles by Professor Harvey R. Brown of Oxford University (he’s the Professor of the Philosophy of Physics there, see http://users.ox.ac.uk/~brownhr/), http://philsci-archive.pitt.edu/archive/00000987/00/Michelson.pdf and http://philsci-archive.pitt.edu/archive/00000218/00/Origins_of_contraction.pdf
The former paper states:
“… in early 1889, when George Francis FitzGerald, Professor of Natural and Experimental Philosophy at Trinity College Dublin, wrote a letter to the remarkable English auto-didact, Oliver Heaviside, concerning a result the latter had just obtained in the field of Maxwellian electrodynamics.
“Heaviside had shown that the electric field surrounding a spherical distribution of charge should cease to have spherical symmetry once the charge is in motion relative to the ether. In this letter, FitzGerald asked whether Heaviside’s distortion result—which was soon to be corroborated by J. J. Thompson—might be applied to a theory of intermolecular forces. Some months later, this idea would be exploited in a letter by FitzGerald published in Science, concerning the baffling outcome of the 1887 ether-wind experiment of Michelson and Morley. … It is famous now because the central idea in it corresponds to what came to be known as the FitzGerald-Lorentz contraction hypothesis, or rather to a precursor of it. This hypothesis is a cornerstone of the ‘kinematic’ component of the special theory of relativity, first put into a satisfactory systematic form by Einstein in 1905. But the FitzGerald-Lorentz explanation of the Michelson-Morley null result, known early on through the writings of Lodge, Lorentz and Larmor, as well as FitzGerald’s relatively timid proposals to students and colleagues, was widely accepted as correct before 1905—in fact by the time of FitzGerald’s premature death in 1901. Following Einstein’s brilliant 1905 work on the electrodynamics of moving bodies, and its geometrization by Minkowski which proved to be so important for the development of Einstein’s general theory of relativity, it became standard to view the FitzGerald-Lorentz hypothesis as the right idea based on the wrong reasoning. I strongly doubt that this standard view is correct, and suspect that posterity will look kindly on the merits of the pre-Einsteinian, ‘constructive’ reasoning of FitzGerald, if not Lorentz. After all, even Einstein came to see the limitations of his own approach based on the methodology of ‘principle theories’. I need to emphasise from the outset, however, that I do not subscribe to the existence of the ether, nor recommend the use to which the notion is put in the writings of our two protagonists (which was very little). The merits of their approach have, as J. S. Bell stressed some years ago, a basis whose appreciation requires no commitment to the physicality of the ether.
“…Oliver Heaviside did the hard mathematics and published the solution [Ref: O. Heaviside (1888), ‘The electro-magnetic effects of a moving charge’, Electrician, volume 22, pages 147–148]: the electric field of the moving charge distribution undergoes a distortion, with the longitudinal components of the field being affected by the motion but the transverse ones not. Heaviside [1] predicted specifically an electric field of the following form …
“In his masterful review of relativity theory of 1921, the precocious Wolfgang Pauli was struck by the difference between Einstein’s derivation and interpretation of the Lorentz transformations in his 1905 paper [12] and that of Lorentz in his theory of the electron. Einstein’s discussion, noted Pauli, was in particular “free of any special assumptions about the constitution of matter”6, in strong contrast with Lorentz’s treatment. He went on to ask:
‘Should one, then, completely abandon any attempt to explain the Lorentz contraction atomistically?’
“It may surprise some readers to learn that Pauli’s answer was negative. …
“[John S.] Bell’s model has as its starting point a single atom built of an electron circling a much more massive nucleus. Ignoring the back-effect of the electron on the nucleus, Bell was concerned with the prediction in Maxwell’s electrodynamics as to the effect on the two-dimensional electron orbit when the nucleus is set gently in motion in the plane of the orbit. Using only Maxwell’s equations (taken as valid relative to the rest frame of the nucleus), the Lorentz force law and the relativistic formula linking the electron’s momentum and its velocity—which Bell attributed to Lorentz—he determined that the orbit undergoes the familiar longitudinal “Fitzgerald” contraction, and its period changes by the familiar “Larmor” dilation. Bell claimed that a rigid arrangement of such atoms as a whole would do likewise, given the electromagnetic nature of the interatomic/molecular forces. He went on to demonstrate that there is a system of primed variables such that the the description of the uniformly moving atom with respect to them is the same as the description of the stationary atom relative to the orginal variables—and that the associated transformations of coordinates are precisely the familiar Lorentz transformations. But it is important to note that Bell’s prediction of length contraction and time dilation is based on an analysis of the field surrounding a (gently) accelerating nucleus and its effect on the electron orbit.12 The significance of this point will become clearer in the next section. …
“The difference between Bell’s treatment and Lorentz’s theorem of corresponding states that I wish to highlight is not that Lorentz never discussed accelerating systems. He didn’t, but of more relevance is the point that Lorentz’s treatment, to put it crudely, is (almost) mathematically the modern change-of-variables, based-on-covariance, approach but with the wrong physical interpretation. …
“It cannot be denied that Lorentz’s argumentation, as Pauli noted in comparing it with Einstein’s, is dynamical in nature. But Bell’s procedure for accounting for length contraction is in fact much closer to FitzGerald’s 1889 thinking based on the Heaviside result, summarised in section 2 above. In fact it is essentially a generalization of that thinking to the case of accelerating bodies. It is remarkable that Bell indeed starts his treatment recalling the anisotropic nature of the components of the field surrounding a uniformly moving charge, and pointing out that:
‘In so far as microscopic electrical forces are important in the structure of matter, this systematic distortion of the field of fast particles will alter the internal equilibrium of fast moving material. Such a change of shape, the Fitzgerald contraction, was in fact postulated on empirical grounds by G. F. Fitzgerald in 1889 to explain the results of certain optical experiments.’
“Bell, like most commentators on FitzGerald and Lorentz, prematurely attributes to them length contraction rather than shape deformation (see above). But more importantly, it is not entirely clear that Bell was aware that FitzGerald had more than “empirical grounds” in mind, that he had essentially the dynamical insight Bell so nicely encapsulates.
“Finally, a word about time dilation. It was seen above that Bell attributed its discovery to J. Larmor, who had clearly understood the phenomenon in 1900 in his Aether and Matter [21]. 16 Indeed, it is still widely believed that Lorentz failed to anticipate time dilation before the work of Einstein in 1905, as a consequence of failing to see that the “local” time appearing in his own (second-order) theorem of corresponding states was more than just a mathematical artifice, but rather the time as read by suitably synschronized clocks at rest in the moving
system. …
“One of Bell’s professed aims in his 1976 paper on ‘How to teach relativity’ was to fend off “premature philosophizing about space and time” 19. He hoped to achieve this by demonstrating with an appropriate model that a moving rod contracts, and a moving clock dilates, because of how it is made up and not because of the nature of its spatiotemporal environment. Bell was surely right. Indeed, if it is the structure of the background spacetime that accounts for the phenomenon, by what mechanism is the rod or clock informed as to what this structure is? How does this material object get to know which type of spacetime Galilean or Minkowskian, say—it is immersed in? 20 Some critics of Bell’s position may be tempted to appeal to the general theory of relativity as supplying the answer. After all, in this theory the metric field is a dynamical agent, both acting and being acted upon by the presence of matter. But general relativity does not come to the rescue in this way (and even if it did, the answer would leave special relativity looking incomplete). Indeed the Bell-Pauli-Swann lesson—which might be called the dynamical lesson—serves rather to highlight a feature of general relativity that has received far too little attention to date. It is that in the absence of the strong equivalence principle, the metric g_μv in general relativity has no automatic chronometric operational interpretation. 21 For consider Einstein’s field equations … A possible spacetime, or metric field, corresponds to a solution of this equation, but nothing in the form of the equation determines either the metric’s signature or its operational significance. In respect of the last point, the situation is not wholly dissimilar from that in Maxwellian electrodynamics, in the absence of the Lorentz force law. In both cases, the ingredient needed for a direct operational interpretation of the fundamental fields is missing.”
Interesting recent comment by anon. to Not Even Wrong:
Even a theory which makes tested predictions isn’t necessarily truth, because there might be another theory which makes all the same predictions plus more. E.g., Ptolemy’s excessively complex and fiddled epicycle theory of the Earth-centred universe made many tested predictions about planetary positions, but belief in it led to the censorship of an even better theory of reality.
Hence, I’d be suspicious of whether the multiverse is the best theory – even if it did have a long list of tested predictions – because there might be some undiscovered alternative theory which is even better. Popper’s argument was that scientific theories can never be proved, only falsified. If theories can’t be proved, you shouldn’t believe in them except as useful calculational tools. Mixing beliefs with science quickly makes the fundamental revision of theories a complete heresy. Scientists shouldn’t start to begin believing that theories are religious creeds.
David Holloway’s book, Stalin and the Bomb, is noteworthy for analysing Stalin’s state of mind over American proposals for pacifist anti-proliferation treaties after World War II. Holloway demonstrates in the book that any humility or good-will shown to Stalin by his opponents would be taken by Stalin as (1) evidence of exploitable weakness and stupidity, or (2) a suspicious trick. Stalin would not accept good will at face value. Either it marked an exploitable weakness of the enemy, or else it indicated an attempt to trick Russia into remaining weaker than America. Under such circumstances (which some would attribute to Stalin’s paranoia, others would call it his narcissism), there was absolutely no chance of reaching an agreement for peaceful control of nuclear energy in the postwar era. (However, Stalin had no qualms about making the Soviet-Nazi peacepact with Hitler in 1939, to invade Poland and murder people. Stalin found it easy to trust a fellow dictator because he thought he understood dictatorship, and was astonished to be double-crossed when Hitler invaded Russia two years later.) Similarly, the facts on this blog post (the 45th post on this blog) and in previous posts, are assessed the same way by the mainstream: they are ignored, not checked or investigated properly. Everyone thinks that they have nothing to gain from a theory based on solid, empirical facts!
Rutherford and Bohr were extremely naive in 1913 about the electron “not radiating” endlessly. They couldn’t grasp that in the ground state, all electrons are radiating (gauge bosons) at the same rate they are receiving them, hence the equilibrium of emission and absorption of energy when an electron is in the ground state, and the fact that the electron has to be in an excited state before an observable photon emission can occur:
“There appears to me one grave difficulty in your hypothesis which I have no doubt you fully realize [conveniently not mentioned in your paper], namely, how does an electron decide with what frequency it is going to vibrate at when it passes from one stationary state to another? It seems to me that you would have to assume that the electron knows beforehand where it is going to stop.”
– Rutherford to Bohr, 20 March 1913, in response to Bohr’s model of quantum leaps of electrons which explained the empirical Balmer formula for line spectra. (Quotation from: A. Pais, “Inward Bound: Of Matter and Forces in the Physical World”, 1985, page 212.)
The ground state energy and thus frequency of the orbital oscillation of an electron is determined by the average rate of exchange of electromagnetic gauge bosons between electric charges. So it’s really the dynamics of quantum field theory (e.g. the exchange of gauge boson radiation between all the electric charges in the universe) which explains the reason for the ground state in quantum mechanics. Likewise, as Feynman showed in QED, the quantized exchange of gauge bosons between atomic electrons is a random, chaotic process and it is this chaotic quanta nature for the electric field on small scales which makes the electron jump around unpredictably in the atom, instead of obeying the false (smooth, non-quantized) Coulomb force law and describing nice elliptical or circular shaped orbits.
‘Ignorance of the law excuses no man; not that all men know the law; but because ’tis an excuse every man will plead, and no man can tell how to confute him.’ – John Selden (1584-1654), Table Talk.
This is one strong nail in the coffin of the mainstream ideas of
1. inflation (to flatten the universe at 300,000 years after the big bang when gravitational effects were much smaller in the cosmic background radiation than you would expect from the structures which have grown from those minor density fluctuations over the last 13,700 million years; we don’t need inflation because the weaker gravity towards time zero explains the lack of curvature then and how gravity has grown in strength since then: traditional arguments used to dismiss gravity coupling variations with time are false because they assume that electromagnetic Coulomb repulsion effects on fusion rates are time-independent instead of similarly varying with gravity, i.e., when gravity was weaker the big bang fusion and later the fusion in the sun wasn’t producing less fusion energy, because Coulomb repulsion between protons was also weaker, offsetting the effect of reduced gravitational compression and keeping fusion rates stable), and
2. force numerical unification to similar coupling constants, at very high energy such as at very early times after the big bang.
The point (2) above is very important because the mainstream approach to unification is a substitution of numerology for physical mechanism. They have the vague idea from the Goldstone theorem that there could be a broken symmetry to explain why the coupling constants of gravity and electromagnetism are different assuming that all forces are unified at high energy, but it is extremely vague and unpredictive because they have no falsifiable theory, nor a theory based upon known observed facts.
What is interesting to notice is that this strong force law is exactly what the old (inaccurate) LeSage theory predicts for with massive gauge bosons which interact with each other and diffuse into the geometric “shadows” thereby reducing the force of gravity faster with distance than the inverse-square law observed (thus giving the exponential term in the equation e-R/s/R2). So it’s easy to make the suggestion that the original LeSage gravity mechanism with limited-range massive particles and their “problem” due to the shadows getting filled in by the vacuum particles diffusing into the shadows (and cutting off the force) after a distance of a few mean-free-paths of radiation-radiation interactions, actually is a clue about the real mechanism in nature for the physical cause behind the short-range of strons and weak nuclear interactions which are confined in distance to the nucleus of the atom! For gravitons, in a previous post I have calculated their mean free path in matter (not the vacuum!) to be 3.10*1077 metres of water; because of the tiny (event horizon-sized) cross-section for particle interactions with the intense flux of gravitons that constitutes the spacetime fabric, the probability of any given graviton hitting that cross-section is extremely small. Gravity works because of an immense number of very weakly interacting gravitons. Obviously quantum chromodynamics governs strong interactions between quarks, but a residue of that allows pions and other mesons to mediate strong interactions between nucleonsHow to censor out scientific reports without bothering to read them
Here’s the standard four-staged mechanism for avoiding decisions by ignoring reports. I’ve taken it directly from the dialogue of the BBC TV series Yes Minister, Series Two, Episode Four, The Greasy Pole, 16 March 1981, where a scientific report needs to be censored because it reaches scientific but politically-inexpedient conclusions (which would be very unpopular in a democracy where almost everyone has the same prejudices and the majority bias must be taken as correct in the interests of democracy, regardless of whether it actually is correct):
Permanent Secretary Sir Humphrey: ‘There’s a procedure for suppressing … er … deciding not to publish reports.’
Minister Jim Hacker: ‘Really?’
‘You simply discredit them!’
‘Good heavens! How?’
‘Stage One: give your reasons in terms of the public interest. You point out that the report might be misinterpreted. It would be better to wait for a wider and more detailed study made over a longer period of time.’
‘Stage Two: you go on to discredit the evidence that you’re not publishing.’
‘How, if you’re not publishing it?’
‘It’s easier if it’s not published. You say it leaves some important questions unanswered, that much of the evidence is inconclusive, the figures are open to other interpretations, that certain findings are contradictory, and that some of the main conclusions have been questioned.’
‘Suppose they haven’t?’
‘Then question them! Then they have!’
‘But to make accusations of this sort you’d have to go through it with a fine toothed comb!’
‘No, no, no. You’d say all these things without reading it. There are always some questions unanswered!’
‘Such as?’
‘Well, the ones that weren’t asked!’
‘Stage Three: you undermine recommendations as not being based on sufficient information for long-term decisions, valid assessments, and a fundamental rethink of existing policies. Broadly speaking, it endorses current practice.
‘Stage Four: discredit the man who produced the report. Say that he’s harbouring a grudge, or he’s a publicity seeker, or he’s hoping to be a consultant to a multi-national company. There are endless possibilities.’
Go to 2 minutes and 38 seconds in the Utube video (above) to see the advice quoted on suppression!
1. A black hole with the electron’s mass would by Hawking’s theory have an effective black body radiating temperature of 1.35*10^53 K. The Hawking radiation is emitted by the black hole event horizon which has radius R = 2GM/c^2.
2. The radiating power per unit area is the Stefan-Boltzmann constant multiplied by the kelvin temperature raised to the fourth power, which gives 1.3*10^205 watts/m^2. For the black hole event horizon spherical surface area, this gives a total radiated power of 3*10^92 watts.
3. For an electron to keep radiating, it must be absorbing a similar power. Hence it looks like an exchange-radiation theory where there is an equilibrium. The electron receives 3*10^92 watts of gauge bosons and radiates 3*10^92 watts of gauge bosons. When you try to move the electron, you introduce an asymmetry into this normal equilibrium and this is asymmetry felt as inertial resistance, in the way broadly argued (for a zero-point field) by people like Professors Haisch and Rueda. It also causes compression and mass increase effects on loving bodies, because of the snowplow effect of moving into a radiation field and suffering a net force.
When the 3*10^92 watts of exchange radiation hit an electron, they each impart momentum of absorbed radiation is p = E/c, where E is the energy carried, and when they are re-emitted back in the direction they came from (like a reflection) they give a recoil momentum to the electron of a similar p = E/c, so the total momentum imparted to the electron from the whole reflection process is p = E/c + E/c = 2E/c.
The force imparted by successive collisions, as in the case of any radiation hitting an object, is The force of this radiation is the rate of change of the momentum, F = dp/dt ~ (2E/c)/t = 2P/c = 2*10^84 Newtons, where P is power as distinguished from momentum p.
So the Hawking exchange radiation for black holes would be 2*10^84 Newtons.
Now the funny thing is that in the big bang, the Hubble recession of galaxies at velocity v = HR implies a force of
F = ma = Hcm = 7*10^43 Newtons.
If that outward force causes an equal inward force which is mediated by gravitons (according to Newton’s 3rd law of motion, equal and opposite reaction), then the cross-sectional area of an electron for graviton interactions (predicting the strength of gravity correctly) is the cross-sectional area of the black hole event horizon for the electron, i.e. Pi*(2GM/c^2)^2 m^2. (Evidence here.)
Now the fact that the black hole Hawking exchange radiation force calculated above is 2*10^84 Newtons, compared 7*10^43 Newtons for quantum gravity, suggests that the Hawking black hole radiation is the exchange radiation of a force roughly (2*10^84)/(7*10^43) = 3*10^40 stronger than gravity.
Such a force is of course electromagnetism.
So I find it quite convincing that the cores of the leptons and quarks are black holes which are exchanging electromagnetic radiation with other particles throughout the universe.
The asymmetry caused geometrically by the shadowing effect of nearby charges induces net forces which we observe as fundamental forces, while accelerative motion of charges in the radiation field causes the Lorentz-FitzGerald transformation features such as compression in the direction of motion, etc.
Hawking’s heuristic mechanism of his radiation emission has some problems for an electron, however, so the nature of the Hawking radiation isn’t the high-energy gamma rays Hawking suggested. Hawking’s mechanism for radiation from black holes is that pairs of virtual fermions can pop into existence for a brief time (governed by Heisenberg’s energy-time version of the uncertainty principle) anywhere in the vacuum, such as near the event horizon of a black hole. Then one of the pair of charges falls into the black hole, allowing the other one to escape annihilation and become a real particle which hangs around near the event horizon until the process is repeated, so that you get the creation of real (long-lived) real fermions of both positive and negative electric charge around the event horizon. The positive and negative real fermions can annihilate, releasing a real gamma ray with an energy exceeding 1.02 MeV.
This is a nice theory, but Hawking totally neglects the fact that in quantum field theory, no pair production of virtual electric charges is possible unless the electric field strength exceeds Schwinger’s threshold for pair production of 1.3*10^18 v/m (equation 359 in Dyson’s http://arxiv.org/abs/quant-ph/0608140 and equation 8.20 in Luis Alvarez-Gaume, and Miguel A. Vazquez-Mozo’s http://arxiv.org/abs/hep-th/0510040). If you check out renormalization in quantum field theory, this threshold is physically needed to explain the IR cutoff on the running coupling for electric charge. If the Schwinger threshold didn’t exist, the running coupling or effective charge of an electron would continue to fall at low energy instead of becoming fixed at the known electron charge at low energies. This would occur because the vacuum virtual fermion pair production would continue to polarize around electrons even at very low energy (long distances) and would completely neutralize all electric charges, instead of leaving a constant residual charge at low energy that we observe.
Once you include this factor, Hawking’s mechanism for radiation emission starts have a definite backreaction on the idea, and to modify his mathematical theory. E.g., pair production of virtual fermions can only occur where the electric field exceeds 1.3*10^18 v/m, which is not the whole of the vacuum but just a very small spherical volume around fermions!
This means that black holes can’t radiate any Hawking radiation at all using Hawking’s heuristic mechanism, unless the electric field strength at the black hole event horizon radius 2GM/c^2 is in excess of 1.3*10^18 volts/metre.
That requires the black hole to have a relatively large net electric charge. Personally, from this physics I’d say that black holes the size of those in the middle of the galaxy don’t emit any Hawking radiation at all, because there’s no mechanism for them to have acquired a massive net electric charge when they formed. They formed from stars which formed clouds of hydrogen produced in the big bang, and hydrogen is electrically neutral. Although stars give off charged radiations, they emit as much negative charge as electrons and negatively charged ions, as they emit positive charge such as protons and alpha particles. So there is no way they can accumulate a massive electric charge. (If they did start emitting more of one charge than another, as soon as a net electric charge developed, they’d attract back the particles whose emission had caused the net charge and the net charge would soon be neutralized again.)
So my argument physically from Schwinger’s formula for pair production is that the supermassive black holes in the centres of galaxies have a neutral electric charge, have zero electric field strength at their event horizon radius, and thus have no pair-production there and so emit no Hawking radiation whatsoever.
The important place for Hawking radiations is the fundamental particle, because fermions have an electric charge and at the black hole radius of a fermion the electric field strength way exceeds the Schwinger threshold for pair production.
In fact, the electric charge of the fermionic black hole modifies Hawking’s radiation, because it prejudices which of the virtual fermions near the event horizon will fall into. Because fermions are polarized in an electric field, the virtual positrons which form near the event horizon to a fermionic black hole will on average be closer to the black hole than the virtual electrons, so the virtual positrons will be more likely to fall in. This means that instead of virtual fermions of either electric charge sign falling at random into the black hole fermion, you instead get a bias in favour of virtual positrons and other virtual fermions of positive sign being more likely to fall into the black hole, and an excess of virtual electrons and other virtual negatively charged radiation escaping from the black hole event horizon. This means that a black hole electron will emit a stream of negatively charged radiation, and a black hole positron will emit a stream of positively charged radiation.
Although such radiation would appear to be massive fermions, because there is an exchange of such radiation in both directions simultaneously once an equilibrium of such radiation is set up in the universe (towards and away from the event horizon), the overlap of incoming and outgoing radiation will have some peculiar effects, turning the fermionic sub relativistic radiation into bosonic relativistic radiation.






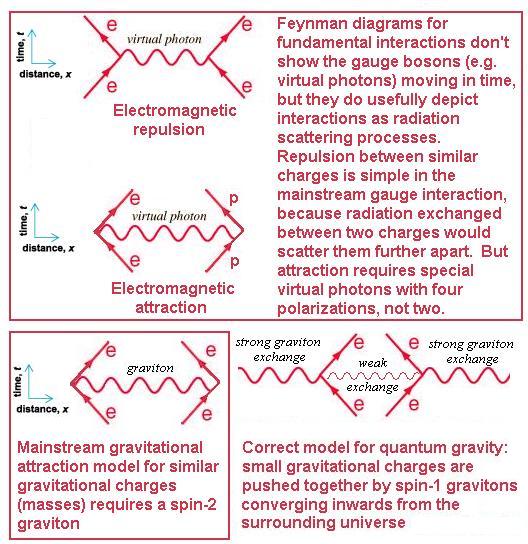
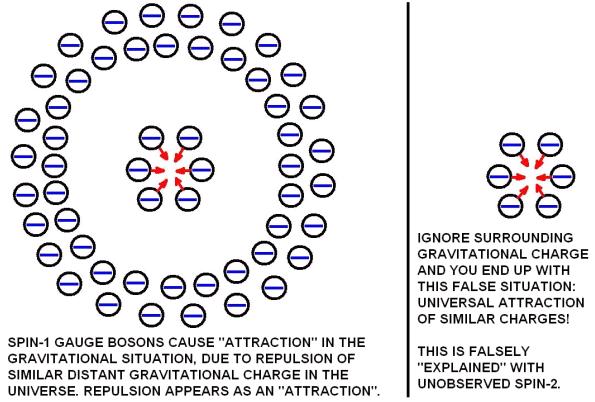

copies of comments submitted to http://groups.google.com/group/sci.physics.foundations/browse_thread/thread/3f0c8c4aa813e990
on uniform and accelerated motion in restricted and general relativity, the radiation of accelerated charges, and the radiation of gravitons by masses to provide the gravitational and inertial spacetime field:
On Jan 3, 9:56 am, David Rutherford wrote:
> An observer in a uniformly accelerating rocket, far from any gravitating
> bodies, observes a light beam projected from a laser from one wall of
> the rocket to the other (perpendicular to the direction of
> acceleration). The observer cannot see outside, so he cannot determine
> his state of motion. Assume that he has been somehow transported to the
> rocket in an unconscious state and wakes up after the rocket has
> attained its uniform acceleration. Consequently, he doesn’t know whether
> he is accelerating or at rest in a uniform gravitational field. The
> light beam will follow a curved path. To what will the observer
> attribute the curvature of the beam?
This is illustrated in Figure 24, “Light propagation in an accelerated rocket” on page 121 of George Gamow’s book, “Gravity” (Dover Publications, Inc., N.Y., 2002 reprint of 1962 edition).
Gamow comments on p. 120: “The observer inside the [rocket] chamber, considering all the phenomena he observes as due to gravity, will conclude from his experiment that the light ray is bent when propagating through a gravitational field. Thus, concluded, Einstein, if the principle of equivalence [between gravitational and other accelerations] is a general principle of physics, light rays from distant stars should be bent if they pass close to the surface of the Sun on the way to a terrestrial observer.”
The curvature of the light beam tells the observer in the rocket that the rocket is in some kind of accelerative field, whether due to resting on the surface of a planet, or due to accelerating under uniform rocket thrust. If the observer could tell it was rocket thrust (rather than terrestrial gravitation) by glancing at the fuel consumption dial or feeling the vibration from the rocket engine, then she would know she was in motion. This is where general relativity differs from restricted (aka “special”) relativity, where non-accelerating motions are relative. Accelerations are absolute:
‘The special theory of relativity … does not extend to non-uniform motion … The laws of physics must be of such a nature that they apply to systems of reference in any kind of motion. Along this road we arrive at an extension of the postulate of relativity… The general laws of nature are to be expressed by equations which hold good for all systems of co-ordinates, that is, are co-variant with respect to any substitutions whatever (generally co-variant). …’ – Albert Einstein, ‘The Foundation of the General Theory of Relativity’, Annalen der Physik, v49, 1916.
‘The great stumbing-block for a philosophy which denies absolute space is the experimental detection of absolute rotation [and other forms of acceleration].’ – Professor A.S. Eddington (who confirmed Einstein’s general theory of relativity in 1919), Space Time and Gravitation: An Outline of the General Relativity Theory, Cambridge University Press, Cambridge, 1921, p. 152.
Only non-accelerating motion is relative, whereas accelerating motion produces forces. In the real world, all motion requires some acceleration to start and stop it, and gravitational fields exist everywhere, so the restricted theory of relativity simply isn’t correct for understanding nature and is only useful for deriving the Lorentz transformation and mass-energy equivalence. It’s like the difference between the Bohr atom and quantum mechanics. The Bohr atom gives you the wrong idea about what happens in the atom, but it is useful in helping to give you simple equations. An observer in a spacecraft would always be able to ascertain the absolute motion of that spacecraft by integrating the absolute accelerations measured from the forces to gyroscopes, which is analogous (but in practice easier) to watching light rays being deflected. Einstein’s 1905 restricted relativity postulate is restricted to uniform, non-accelerating motion, and therefore doesn’t apply to any real physical situations in this particular universe we inhabit where motions are due to acceleration and where there are gravitational fields (gravitons) causing acceleration.
****************************************
On Jan 3, 9:30 pm, Bob_for_short wrote:
> An accelerating reference frame is NOT equivalent to a gravitational
> field, even locally.
> In a gravitational field a falling charge radiates, in an accelerating
> reference frame it does not. On the contrary, there a “resting” charge
> radiates. If you look outside your rocket, you will see the whole
> universe accelerating, so it is not at all equivalent to some “local”
> gravity.
In any kind of quantum gravity theory, gravitational charge will be exchanging gravitons, which are the field quanta. So you need to say what kind of charge and what kind of radiation you refer to. I’m assuming you are just thinking of classical electromagnetic radiation from an accelerating electric charge like an electron. Actually, an electron decelerates when it radiates energy as electromagnetic waves. If you want an electron to accelerate, you also need to supply it with energy in the form of electromagnetic radiation. Think about an antenna on a radio transmitter. The supplied field carried by the conducting antenna causes the electron to accelerate, which in turn causes the electron to radiate.
In the case of an electric charge being accelerated by a gravitational field, gravitons supply energy and some of that energy is then radiated as electromagnetic waves. Let’s quantify this process to see how the numbers go for non-relativistic electron fall velocities (i.e. well below c).
A falling electron released in a uniform gravitational acceleration, g, gains velocity v = gt.
Kinetic energy, E = (1/2)mv^2 = (1/2)m(gt)^2
Hence after 1 second, an electron in freefall gains a maximum (ignoring electromagnetic radiation) of 4.4*10^(-29) Joules.
Electromagnetic energy is radiated whenever there is acceleration of electric charge, as given by Larmor’s non-relativistic formula for radiated power: P = [(qg)^2]/[6*{Pi}*{Permittivity of free space}*c^3] watts, where q is charge and g is the acceleration of that charge.
Hence, the freefalling electron in terrestrial gravity, g = 9.81 ms^(-2), radiates 5.5*10^(-52) watts. Since a watt is 1 Joule per second, over the first second of fall an electron radiates 5.5*10^(-52) Joules.
Thus, the proportion of its kinetic energy after 1 second [4.4*10^(-29) J] which is radiated as electromagnetic radiation [5.5*10^(-52) ms^(-2) J] is only [5.5*10^(-52)]/[4.4*10^(-29)] = 1.3*10^(-23). This radiated electromagnetic energy is a trivial proportion of the kinetic energy that the electron gains from the gravitational acceleration.
In quantum gravity, accelerations are due to the unequal exchange of gravitons radiated by masses, while uniform motions occur where there is an equilibrium of graviton exchange. This would apply to mainstream spin-2 graviton conjecture by Pauli and Fietz, as well as any other graviton spin (there is a severe problem with the spin-2 graviton ideas, as it pretends that only two masses radiate gravitons in the universe, and uses this falsehood to prove than spin-2 is needed to get universal attraction between similar charge as Zee uses in his QFT textbook; but if you accept the simple fact that there is a lot of mass in the universe around us and no mechanism exists to stop graviton exchanges with all that mass, then your two similar gravitational charges are accelerated together by the converging spin-1 graviton flux from the immense mass in the surrounding universe which exceeds the repulsion due to spin-1 gravitons exchanged between the two masses in question, see https://nige.wordpress.com/2008/01/30/book/ ).
> In a gravitational field a falling charge radiates, in an accelerating
> reference frame it does not. On the contrary, there a “resting” charge
> radiates.
I disagree with this. A resting charge (relative to an observer) is not going to radiate energy, or the principle of conservation of energy will be violated. Where does the supposed radiated energy come from? An accelerating charge in any gravitation or other accelerating field (e.g. where an electron is accelerated by an electric field carried by a conductor) will radiate. A resting charge will not observably radiate in the frame of reference in which it is observed to be resting.
For an insight into the current mainstream viewpoint held by string theory skeptic Dr Woit, please see the comment about Dirac’s condemnation of purely mathematical (non-dynamical) quantum field theory fiddles on his Not Even Wrong weblog, and his reaction to it:
http://www.math.columbia.edu/~woit/wordpress/?p=1487&cpage=1#comment-46445
anon. says:
January 6, 2009 at 9:56 am
Thanks for the link to Farmelo’s book on Dirac. I’m surprised that you are keen to read about the guy, seeing how much he argued against mainstream QFT developments after his own work. (E.g., quotations from Dirac here and here.) Dirac also claimed that there was some argument for a physical Dirac sea of virtual particles in the vacuum:
‘Physical knowledge has advanced much since 1905, notably by the arrival of quantum mechanics, and the situation has again changed. If one examines the question in the light of present-day knowledge, one finds that the aether is no longer ruled out by relativity, and good reasons can now be advanced for postulating an æther. . . .
‘We must make some profound alterations to the theoretical idea of the vacuum. . . . Thus, with the new theory of electrodynamics we are rather forced to have an æther.’ – P. A. M. Dirac, ‘Is There an æther?’, Nature, v168 (1951), pp. 906-7.
‘Infeld has shown how the field equations of my new electrodynamics can be written so as not to require an æther. This is not sufficient to make a complete dynamical theory. It is necessary to set up an action principle and to get a Hamiltonian formulation of the equations suitable for quantization purposes, and for this the æther velocity is required.’ – P. A. M. Dirac, ‘Is there an æther?’, Nature, v169 (1952), p. 702.
In addition, there was his large numbers hypothesis with the argument that G varies with time. In addition, he was an electrical engineer before studying mathematics. Surely all this crackpottery makes the guy unworthy of serious attention?
Dr Woit’s response:
http://www.math.columbia.edu/~woit/wordpress/?p=1487&cpage=1#comment-46447
Peter Woit says:
January 6, 2009 at 11:19 am
anon.,
Adopting the standard of ignoring any of the great physicists of the past if some of their ideas don’t hold up well half a century later would make the study of the history of physics a great deal simpler…
Also missing the essential point was physicist Thomas Larsson who added:
http://www.math.columbia.edu/~woit/wordpress/?p=1487&cpage=1#comment-46464
Thomas Larsson says:
January 7, 2009 at 2:54 am
Scientists are not remembered for their mistakes and blunders, but for their successes. The list of great physicists doing fundamental mistakes is long. E.g., Lorentz and Poincare were leaders in ether theory, Kelvin ridiculed Einstein’s discoveries, Einstein denied QM, Heisenberg’s Urfeld [Unified?] theory, Witten promoted string theory 🙂 , and many others. The only safe way to avoid wrong ideas is to not have any ideas at all.
The point being made was that virtual particles are the essential feature of quantum field theory, and for a dynamical theory of physics you therefore need a physical spacetime fabric, i.e. you need mathematical models of physical processes going on the the vacuum (gauge bosons being exchanged between charges to create force-field effects like strong and weak forces, gravity, magnetism, electric fields, etc.), not merely mathematical models of a vacuum composed of nothing.
It’s amazing and depressing that prejudice is so ingrained that Dirac’s quoted arguments make no ripple or echo on that score! The reason why Dirac promoted a physical particle spacetime fabric instead of merely stripped down mathematical models was probably because he learned about electric polarization phenomena and the mechanisms at play in real physical situations when studying electrical engineering before he did mathematics and came up with the Dirac equation of quantum field theory! Today’s ‘modern physicists’ are really just physically-ignorant mathematicians who worship a belief in a purely mathematical univerese, and have less than damn-all interest in physical mechanisms; they actually want to sneer at real (mechanistic) physics, and to rename equations as ‘physics’.
Notice that the second letter by Dirac to Nature (1952) quoted above is in response to a letter from Einstein’s friend and former assistant Leopold Infeld to Nature which attempted to criticise Dirac’s earlier paper in 1951 in Nature. Infeld claimed that Dirac didn’t understand his own equation, and that it didn’t need an ether:
‘Infeld has shown how the field equations of my new electrodynamics can be written so as not to require an æther. This is not sufficient to make a complete dynamical theory. It is necessary to set up an action principle and to get a Hamiltonian formulation of the equations suitable for quantization purposes, and for this the æther velocity is required.’ – P. A. M. Dirac, ‘Is there an æther?’, Nature, v169 (1952), p. 702.
In 1938, Infeld had admitted his prejudice about the ether in his book, co-authored with Einstein (in order to give the American authorities a reason to admit Infeld into the United States and save him from Nazi concentration camps since he was a Jew), Evolution of Physics:
‘Looking back at the development of physics, we see that the ether, soon after its birth, became the enfant terrible of the family of physical substances. … We shall say our space has the physical property of transmitting waves and so omit the use of a word we have decided to avoid. The omission of a word from our vocabulary is of course no remedy; the troubles are indeed much too profound to be solved in this way. Let us now write down the facts which have been sufficiently confirmed by experiment without bothering any more about the ‘e—r’ problem.’
– Albert Einstein and Leopold Infeld, Evolution of Physics, 1938, pp. 184-5 (the book which was written to get Infeld out of Nazi Germany and accepted as a worthy refugee in America).
Notice that Einstein wrote earlier:
‘The special theory of relativity … does not extend to non-uniform motion. The laws of physics must be of such a nature that they apply to systems of reference in any kind of motion. Along this road we arrive at an extension of the postulate of relativity. The general laws of nature are to be expressed by equations which hold good for all systems of co-ordinates, that is, are co-variant with respect to any substitutions whatever (generally co-variant).’
– Albert Einstein, The Foundation of the General Theory of Relativity, Annalen der Physik, v49, 1916.
‘Recapitulating, we may say that according to the general theory of relativity, space is endowed with physical qualities… According to the general theory of relativity space without ether is unthinkable.’ – Albert Einstein, Leyden University lecture on ‘Ether and Relativity’, 1920. (Einstein, A., Sidelights on Relativity, Dover, New York, 1952, pp. 15, 16, and 23.)
The point Einstein is making here is essentially that current teaching of general relativity, as causing a flat surface like a rubber sheet to curve into a manifold, is unhelpful to further progress in unifying quantum space with gravitation, since physical space fills volume, not surface area.
“… the electromagnetic coupling grows with energy… the polarisation of the vacuum [ether consists of the process of pair production of virtual] … electron-positron pairs around the location of the [core of the electric] charge. These virtual pairs behave as dipoles that, as in a dielectric medium, tend to screen this charge … decreasing its value at long distances (i.e. lower energies).”
– Luis Alvarez-Gaume and Miguel A. Vazquez-Mozo, Introductory Lectures on Quantum Field Theory, arXiv.org hep-th/0510040 v1, 5 October 2005, p. 71 (also see in particular pp 70-71, and pp 83-85).
‘The Michelson-Morley experiment has thus failed to detect our motion through the aether, because the effect looked for – the delay of one of the light waves – is exactly compensated by an automatic contraction of the matter forming the apparatus [and the Lorentz contraction itself is physically caused by the head-on pressure of the ether against the front of the moving particle, squeezing it slightly in the direction of motion, by analogy to ideal-fluid frictionless equivalent of the impact and recoil forces of air hitting on the nose of a moving aircraft or water hitting the bows of a moving ship; because the ether can’t carry away energy unless there is acceleration – when you get radiation emission carrying away energy – there is no continuous drag force from the ether, just a resistance to accelerations which we call inertia, and this is the key difference between air or water composed of real particles and ether composed of virtual particles] …. The great stumbing-block for a philosophy which denies absolute space is the experimental detection of absolute rotation.’
– Professor A.S. Eddington (who confirmed Einstein’s general theory of relativity in 1919), MA, MSc, FRS, Space Time and Gravitation: An Outline of the General Relativity Theory, Cambridge University Press, Cambridge, 1921, pp. 20, 152.
‘Some distinguished physicists maintain that modern theories no longer require an aether … I think all they mean is that, since we never have to do with space and aether separately, we can make one word serve for both, and the word they prefer is ‘space’.’
– A.S. Eddington, New Pathways in Science, v2, p39, 1935.
‘It seems absurd to retain the name ‘vacuum’ for an entity so rich in physical properties, and the historical word ‘aether’ may fitly be retained.’
– Sir Edmund T. Whittaker, A History of the Theories of the Aether and Electricity, 2nd ed., v1, p. v, 1951.
‘It has been supposed that empty space has no physical properties but only geometrical properties. No such empty space without physical properties has ever been observed, and the assumption that it can exist is without justification. It is convenient to ignore the physical properties of space when discussing its geometrical properties, but this ought not to have resulted in the belief in the possibility of the existence of empty space having only geometrical properties… It has specific inductive capacity and magnetic permeability.’
– Professor H.A. Wilson, FRS, Modern Physics, Blackie & Son Ltd, London, 4th ed., 1959, p. 361.
‘The idealised physical reference object, which is implied in current quantum theory, is a fluid permeating all space like an aether.’
– Sir Arthur S. Eddington, MA, DSc, LLD, FRS, Relativity Theory of Protons and Electrons, Cambridge University Press, Cambridge, 1936, p. 180.
‘In many interesting situations … the source of the gravitational field can be taken to be a perfect fluid…. A fluid is a continuum that ‘flows’… A perfect fluid is defined as one in which all antislipping forces are zero, and the only force between neighbouring fluid elements is pressure.’
– B. Schutz, General Relativity, Cambridge University Press, Cambridge, 1986, pp. 89-90
copy of a comment:
http://dorigo.wordpress.com/2009/01/27/information-control-from-cern/#comment-104133
‘I think that scientific results on basic science do not belong to their discoverers, nor to the experimental collaboration: they, as much as the data they are based upon, belong to the people.’ – Tommaso
‘Discoverers are owners of the valuable ideas they discover, they deserve the credit, they deserve the profit coming out of this credit, and they deserve to be celebrated by generations of science fans and others.
‘The situation is completely analogous to the ownership of any other thing. The private ownership of these things is both a moral principle per se as well as a crucial motivation that makes the potential discoverers – and capitalists – care. It partly motivates them to work. If the profit of the people were the only positive thing for them and they would have nothing person-specific out of the discoveries, they would almost certainly leave it to others.
‘They must have the pleasure of finding things out, which is a private feeling, not a feeling that belongs to the people, and this pleasure has additional consequences that belong to the individuals, too.’ – Luboš
I always believed in the romantic tale that scientists were beyond the corruption of monetary prizes and rewards, because were just seeking factual knowledge. (E.g., the tales of Copernicus and Galileo being in trouble for heresy, and getting relatively little in the way of prizes, money, or public praise. They didn’t ‘leave it to others’ because it was financially unprofitable!) Politics, warfare and even sadly some sports are, by contrast, competitive races, where people want to win big prizes and fame by way of beating their human opponents.
Luboš is correct, and science is mainly motivated by capitalist greed, just like everything else. It’s interesting that the communist U.S.S.R. succeeded with the first satellite Sputnik and the first man in space. Presumably the scientists behind those advances were motivated by other considerations than fame and money. But it’s a nice finishing touch that – after first making the case for science being a capitalist activity – Luboš then adds that scientists should also derive some pleasure just from making discoveries.
http://dorigo.wordpress.com/2009/01/27/information-control-from-cern/#comment-104140
‘Scientists are human beings and they of course seek a decent salary.’
Hi Tommaso, I’m sorry you found something unsatisfactory. I don’t think you are inspired by capitalist motives. But generally mainstream science is changed from the situation where Dalton, Einstein and others could work as teachers or patent examiners and do physics as a spare-time hobby, making little money from it. I agreed with Luboš that nowadays, if scientists gained ‘nothing person-specific out of the discoveries, they would almost certainly leave it to others’, because I think high energy theoretical physics is losing its momentum. It’s great that you enjoy your work, and were prepared to take a much lower salary to do the scientific research you wanted to do.
copy of a comment to Professor Clifford Johnson’s blog Asymptotia:
http://asymptotia.com/2009/02/03/so-what-is-string-theory-anyway/#comment-130198
Nige Cook
February 5, 2009 at 12:17 am
‘So what do we put on the T-shirt? (You know, the analogue of Maxwell’s equations for electromagnetism – light, etc – that every physics undergrad likes to have on their T-shirt). Well, we don’t know yet.’
The candour is nice. If string theorists were working on an alternative to a mainstream idea (instead of being the mainstream), and they admitted that they couldn’t even define their theory, they might have a tough time being taken seriously. Alternatives are shunned by string theorists: authors are told by peer-reviewers to go away, solve their problems, and come back when they have the theory completed to a more understandable level.
This double-standard, where mainstream work on string theory is taken seriously and published, but alternative ideas with few people working on them are rejected (simply because they are not fashionably mainstream and haven’t had the same investment of time as string theory has) creates critics with axes to grind.
The usual defence of string theory is that so many people have worked on it for so long and published so much, and have all these indirect successes like the CFT/AdS equivalence conjecture and lots of other applications from it, but you can get such useful spin-offs from failed theories. E.g., Ptolemy’s epicycles theory of the earth-centred universe was so complicated it was a major motivation that led to the development of trigonometry to simplify the calculations, but this result doesn’t justify the epicycle theory as solid physics.
It’s quite possible that more spin-offs would have occurred if people had taken the more nearly correct solar system theory of Aristarchus more seriously (in it’s original form it had errors such as circular orbits), and worked on that instead of dismissing it out of hand! Trigonometry would probably still have arisen.
Copy of a comment to Asymptotia:
http://asymptotia.com/2009/02/05/another-approach/#comment-130213
Nige Cook
February 5, 2009 at 3:42 am
Thanks for this! Is the claim in the second row of the cartoon (that string theory is only formulated perturbatively) really a serious objection to the theory? Surely quantum field theory itself is only formulated in a useful way (for making checkable predictions) as a perturbative expansion, e.g. the expansion of a path integral into increasingly higher order terms with correspondingly complex Feynman diagrams having more and more interaction vertices, with more and more ‘loops’ of virtual particles appearing and annihilating and thereby affecting the basic interaction of the diagram.
How could there be a non-perturbative formulation of the theory, when pair-production/annihilation loops in spacetime are a reality? there are an infinite number of ways you can add loops to a Feynman diagram to make it more and more complex, and the pair production particles so introduced perturb the interaction results. So a non-perturbative formulation would have to ignore the effects of these loops, and so would not be dealing with the physics of the real world.
The background independence criterion is nicely explained by quantum field theorists Luis Alvarez-Gaume and Miguel Vazquez-Mozo in Introductory Lectures on Quantum Field Theory, http://arxiv.org/PS_cache/hep-th/pdf/0510/0510040v2.pdf page 85, precisely because the the virtual particles in the vacuum have different effects depending on the motion of the observer:
‘… it is not possible anymore to define a state which would be recognised as the vacuum by all observers. This is precisely the situation when fields are quantized on curved backgrounds. … if the background is time-dependent … different observers will observe different vacuum states. As a consequence, what one observer calls the vacuum will be full of particles for a different observer.’
So if it’s true that string theory only describes perturbative expansions in fixed spacetime backgrounds, that must be depressing!
String investigator Clifford deleted the facts and turned to a personal attack (my comment was correct and quoted the facts), but never mind:
http://asymptotia.com/2009/02/05/another-approach/#comment-130238
Nige Cook
February 5, 2009 at 8:47 am
[…snip, snip, snipping out of a long, long bit saying just plain wrong stuff about quantum field theory and string theory that is totally misleading, and largely off the topic of the thread. Sorry. -cvj]
Sorry I got it wrong again!
Nige
Clifford also on the other thread responded with the incorrect claim:
http://asymptotia.com/2009/02/03/so-what-is-string-theory-anyway/#comment-130199
Clifford
February 5, 2009 at 12:29 am
No, no, no – the usual defence of string theory is its rather interesting and promising results in several areas that a lot of people are interested in. Plain and simple. And people working on string theory love alternatives. If something better comes along (and you’re free to present it to the community through the usual channels), the community would start working on that overnight.
See all this laid out plainly in the earlier discussions I’ve pointed to in the post. No point rehashing it all here.
-cvj
It is clear that the string investigators (Clifford is one of the most helpful) are either being dishonest about the nature of the hostility to new ideas which make checked, confirmed predictions, or they are deluded with the false belief that they are friendlier human beings than they really are.
I had the experience of having my inner ears filled with fluid as a kid due to blocked eustachian tubes, which meant that the fluid attenuated all but the lowest frequencies. This meant that (1) I couldn’t hear properly (many words sound similar and indistinguishable when you chop off the higher frequencies), and (2) because you learn to speak by copying sounds you hear, it affected my speech too. Medically qualified people who should have known better thought I simply needed speech lessons, and so it was years before I was eventually diagnosed and had drainage holes surgically made in my eardrums.
The point is, something as simple as this really shows you what human nature is like. The majority of people, both kids and teachers, just assume that you are stupid. In fact, because you can’t hear properly and are embarrassed to speak and ask questions – because you get mimicked afterwards – you really are unable to learn as easily as the others for purely physical reasons in class. It makes the school experience extremely unproductive and unpleasant for years.
So a very small difficulty in communication leads to massive knock-on problems! If people were really as immensely intelligent and as decent at heart as is widely made out to be the case, you wouldn’t get such problems lasting for years. The cause would be quickly diagnosed and quickly treated by the massively intelligent people, and you wouldn’t be treated with contempt for having these problems. In the real world, this isn’t the case.
My feeling is that this problem as a kid was a blessing because it spelled out clearly what human nature really is like. It’s like Newton’s 3rd law of motion. For every onward action, there’s an equal and opposite reaction kicking back. You can’t expect people to do what is right because of (alleged) intelligence or (alleged) nicety. Prejudices, as useful shortcuts, are simply too tempting in busy lives. This is why Dyson’s personal finding (based on his incredibility difficulty in getting Feynman’s work taken seriously by J. R. Oppenheimer) is so true:
‘… At any particular moment in the history of science, the most important and fruitful ideas are often lying dormant merely because they are unfashionable. Especially in mathematical physics, there is commonly a lag of fifty or a hundred years between the conception of a new idea and its emergence into the mainstream of scientific thought. If this is the time scale of fundamental advance, it follows that anybody doing fundamental work in mathematical physics is almost certain to be unfashionable. …’
– Professor Freeman Dyson, Unfashionable Pursuits, 1981(reprinted in ‘From Eros to Gaia’, Penguin 1992, at page 171), cited by Tony Smith at http://valdostamuseum.org/hamsmith/goodnewsbadnews.html
Contrast this observation of Dyson’s with Clifford’s claim (quoted in a comment above):
‘… people working on string theory love alternatives. If something better comes along (and you’re free to present it to the community through the usual channels), the community would start working on that overnight.’
If that were true, then long ago the gauge theory of quantum gravity would have been investigated by the mainstream. In fact, the U.K. Institute of Physics editor of the peer-reviewed journal Classical and Quantum Gravity sent my paper for review about a decade ago before submissions went electronic, and he sent me a copy of the peer-reviewer report (with the reviewer name omitted) which stated that the paper was not connected to string theory and so was inappropriate for publication because string theory was hyped as being the theory of quantum gravity (spin-2 graviton framework). It did not make any comments about the physics in my paper.
Clifford then launched into a further personal style ad hominem attack (‘you seem to have a way of saying with the appearance of great authority a number of things about very standard techniques and ideas in physics that are just, I’m sorry to have to say, utterly incorrect’), still ignoring my comment and making up incorrect statements about what I had stated, so I responded:
http://asymptotia.com/2009/02/05/another-approach/#comment-130241
Clifford
February 5, 2009 at 9:35 am
Hi Clifford, actually I asked a question, and quoted as evidence http://arxiv.org/abs/hep-th/0510040v2 as it’s online, rather than any of the other QFT textbooks I’m studying. But of course the thread is a joke not to be questioned, and I misbehaved for asking a physics question about it. Sorry again!
One example of a so-called non-perturbative quantum field theory formulation is lattice gauge theory, where a computer simulation is done to model quantum field effects in order to try to predict hadron masses, which perturbative quantum field theory doesn’t do because the perturbative expansion is divergent or at least non-converging (i.e., the infinite series of successive terms in the expansion don’t get smaller fast enough to allow you can get a good approximation by just taking the first few terms and ignoring the rest, which is what is done for calculating things like the magnetic moment of leptons very accurately).
However, the lattice gauge theory efforts are not the most impressive successes of quantum field theory. Hadron masses calculated that way have considerable errors in comparison to the accuracy of perturbative expansion calculations of quantum electrodynamic checks like the magnetic moments of leptons, Lamb shift, etc.
In addition, although lattice gauge theory is called a non-perturbative method, that’s a misleading claim which assumes that “perturbative” gauge theory only refers to situations where a converging perturbative expansion is used.
In fact, virtual particles cause perturbation in any given particle interaction, and there is perturbation present even in lattice gauge theory where virtual particles like gluons and virtual fermions polarize in fields, which physically causes a perturbation affecting the field (either shielding it or increasing its strength) that would not occur in the absence of such virtual partiles.
Therefore, although lattice gauge theory is an alternative to summing a few terms in a mathematical perturbative expansion, it is not physically a describing a situation where perturbation effects of quantum fields are absent. Virtual particles cause perturbative effects regardless of how you mathematically model them; whether you are using a perturbative expansion that converges quickly and adding the first few terms to get a good approximation, or whether you are using a so-called (misnomer) “non-perturbative” (actually “non-perturbative expansion based”) method like a lattice gauge theory.
The lack of clear physical understanding by mainstream workers in quantum field theory of virtual particle processes which are being mathematically modelled is precisely the reason why the subject has stagnated with the shambles of string “theory”: if they modelled observed physical processes using quantum fields of gauge boson exchange radiation, with a proper understanding from Schwinger that pair production/annihilation (spacetime loops of virtual bosons and virtual fermions) requires very strong fields close to particle cores (e.g. 1.3*10^18 volts/metre field strength as calculated by Schwinger for pair production) they would arrive at the answers, e.g. the fact that gauge boson radiation in most of the vacuum of the universe is simpole and doesn’t have loops because the field strengths are below Schwinger’s threshold for pair production. Hence, the vacuum for the most part is relatively simple; it doesn’t have complex loops and so it can be modelled by a simple non-perturbative summation such as the geometry in figure 1 of this blog post.
Instead of seeing this simplicity, they’re obsessed with high-energy (Planck scale) unification of fundamental forces, which hasn’t been observed, is unobservable, and leads to extradimensional unobserved speculations. It’s really a religious problem (belief in unobserved spin-2 gravitons, extra spatial dimensions, branes, etc.), a cultural problem (groupthink) or a political problem (censorship of critics and alternative ideas), or maybe a combination of all three, but it is not a physics problem in the sense that you can’t use physics to reason with bigotry. They won’t listen. They have their own definition of physics which is a community bandwaggon activity, and they don’t like or really want to hear others.
copy of a relevant comment to an earlier post:
https://nige.wordpress.com/2007/01/21/hawking-and-quantum-gravity/
Yoshiro Aoki,
Thank you for your comment.
Spacetime is a mathematical concept, not a physical reality: there is no spacetime physically, just quantum fields which produce effects that can be approximated on large scales by mathematical idealization of distorted geometry, the curvature of spacetime. The exchange of field quanta between charges causes the force effects of gravity. The spacetime continuum is just a classical approximation to this. Spacetime isn’t physically real. The fabric of the vacuum is quantum fields.
Therefore, when you write that spacetime is stretched out, you are mixing up the mathematical approximation (spacetime) with the reality. In reality, there are quantum fields. These fields aren’t stretched out like elastic as the universe expands: instead, they cause the expansion of the universe itself because the exchange of field quanta induce acceleration of charges away from each other.
Please try reading the latest post on this blog, and see if it helps: https://nige.wordpress.com/2008/12/20/summary-explanation-of-some-non-mainstream-quantum-gravity-evidence/
copy of a comment to Arcadian Functor:
http://kea-monad.blogspot.com/2009/02/quote-of-month.html
Yes, that’s the depressing reality of how string theorists see themselves, as the sole brave sailors on an otherwise deserted sea! I wrote a comment which replied to that, but Dr Woit deleted it. ‘Somebody’ (a string theory defender) wrote:
‘… almost all the ideas that seemed promising, seem to arise naturally in string theory. Supergravity, kaluza-klein theories, etc. were separate ideas initially, but they arise automatically in string theory.’
These people in their own deluded world must somehow see supergravity and kaluza-klein speculations as good ideas, not failures. The ideas connected by string theory are just fashionable speculations which are not even wrong. That they initially ‘seemed promising’ has nothing to do with science, because of the very long, well-known list of totally misleading ideas that initially ‘seemed promising’ and became orthodoxy, but then contributed to the censoring of the correct ideas which had to struggle to get attention (flat earth, genesis, epicycles, caloric, phlogiston, etc. …). Nature is ‘subtle’, as Einstein observed. The ideas that get immediate limelight aren’t always right. This is the problem.
Instead of the fashionably ‘even mildly promising alternative’ idea being the only one to deserve any attention, it is often the idea that looks unfashionable, and hence less promising to mainstream wags, that is right.
Unfashionable (i.e. new) ideas that are radical, are unfamiliar and often unpromising in their nascent form to the busy mainstream, and are often censored at first, even if they turn out to be correct later on, as the history of science shows.
String theorists define ‘promising new ideas’ as more uncheckable speculations that link to existing fashionable speculations in string theory. This view of what ‘promising’ means isn’t scientific.
As Tony Smith has pointed out, the problem of fashionable pursuits in physics led Freeman Dyson to declare:
‘… At any particular moment in the history of science, the most important and fruitful ideas are often lying dormant merely because they are unfashionable. Especially in mathematical physics, there is commonly a lag of fifty or a hundred years between the conception of a new idea and its emergence into the maintsream of scientific thought. If this is the time scale of fundamental advance, it follows that anybody doing fundamental work in mathematical physics is almost certain to be unfashionable. …’
– Dyson’s 1981 essay, Unfashionable Pursuits
The point made is that all alternative ideas radical enough to have any chance of being helpful are also radical enough to be dismissed by today’s mainstream.
Dyson is also on video with the example of QED here (Dyson says that leading physicist Oppenheimer at Pocono in 1948 was a ‘bigoted old fool’ who could not immediately grasp Feynman’s path integrals at Pocono in 1948, and instead Oppenheimer kept finding trivial reasons in the wording of the theory to dismiss it as nonsense, trying to prevent any communication of ideas, i.e. to censor Feynman’s work). If that could have happened to Feynman, it can happen to any alternative ideas that are radical enough to be useful alternatives!
The best example is of course Feynman’s path integral formulation which was dismissed by Teller, Bohr, Dirac and Oppenheimer until Dyson and Bethe eventually won them over at Pocono in 1948.
Tony Smith (this link to a Google cache since his server seems to be down at present), whose new work is now censored from arXiv, has quoted The Beat of a Different Drum: The Life and Sciece of Richard Feynman where Feynman explains that the problem was not just Oppenheimer. Teller dismissed it because it ignored the exclusion principle, Dirac dismissed it because it didn’t have a unitary operator, and Bohr dismissed it because he claimed Feynman didn’t know the uncertainty principle, and claimed that the uncertainty principle dismissed any notion of path integrals representing the trajectory of an electron! Feynman concluded: ‘it didn’t make me angry, it just made me realize that … [ they ] … didn’t know what I was talking about, and it was hopeless to try to explain it further.’ Feynman in 1985 in his book QED explained clearly in a footnote that the uncertainty principle is not a separate law from path integrals so Bohr’s objection was invalid; interferences due to random virtual particle exchanges cause the uncertainty.) But if this dismissal from numerous top experts can happen to Feynman’s path integrals, it surely can happen to any radical-enough-to-be-helpful quantum gravity ideas!
Another issue with the claim by ‘Somebody’ at the Not Even Wrong weblog that
‘It is not like there are tons of alternatives out there and theorists are ignoring them. … The self-interest of theorists motivates them to consider new promising ideas very seriously. I don’t even know one promising alternative idea out there which is not getting the attention it deserves.’
is the sheer arrogance of claiming that because ‘Somebody’ admits to being ignorant of the existence of one promising alternative, this admission of ignorance is somehow to be construed as praiseworthy clever evidence that no such alternative exists! Duh!
It’s a bit like Oppenheimer throwing Feynman’s paper into the lavatory in 1948, and then stating that he has seen no promising ideas out there. Yeah, right!
Clever political spin trick. If string theory does ever go bankrupt, will its practitioners get jobs in the Ministries of Propaganda for third world dictatorships? How is it that so many people are taken in by this spin?
Dr Woit has written that he thinks that supergravity looks promising, so maybe that’s why he deleted my comment. I liked Dr Woit’s idea in his 2002 paper that people should be looking to see what kind of gauge group quantum gravity should have, i.e. how do you add to U(1)xSU(2)xSU(3) to include quantum gravity? But, as with Smolin, he is quite proud of mainstream affiliations where it suits him. Neither is radical enough to investigate the full spectrum of promising ideas or back them. For various reasons, they spend time investigating ideas that generate a lot of mathematical speculation but little connection to experiment, i.e. analogies to the failure of string theory.
Thank you for this interesting article, and the book and lecture references.
copy of a comment:
http://kea-monad.blogspot.com/2009/02/quote-of-month.html
Anonymous,
For an example of peer-reviewed published paper unifying U(1) electromagnetism with gravity, see Lunsford’s paper Int. J. Theor. Phys. 43 , 1 (2004) 161-177. Lunsford states on the Not Even Wrong blog that this peer-reviewed and published paper was deleted from arXiv.org by the mainstream stringy censors there, effectively preventing any further developments or discussions of that theory in the ‘proper’ places! This is what happens in the mainstream string theory culture! It’s inevitable that since string theory fails to achieve anything real, it must defend itself instead by censoring out alternative ideas and stagnating the rest of the field so it stands out as being alone. (Sinking all the other ships with torpedos, and then claiming to be the only people brave enough to set sail!)
But this is just one example and Kea is doing research into quantum gravity using category theory which is another direction. Such work is usually ignored by the mainstream, or where it is not ignored, it is generally dismissed as unfashionable, or claimed to be wrong by people who don’t understand it.
copy of a relevant comment:
https://nige.wordpress.com/2007/01/21/hawking-and-quantum-gravity/
Hi Yoshiro Aoki,
Thank you for your comments.
‘I am aware of the nature of the vacuum as quantum fields, but are not the shape of these fields related directly to mass present (or not present) within them, or equivalently by a mass in motion?’
The field is composed of field quanta, gauge bosons which are exchanged between charges to produce forces. Particles (gravitons) are therefore being exchanged between masses to produce gravity. In classical theory like general relativity, you have shapes of fields given by plotting field lines. However, such field lines need to be replaced by quanta exchanges.
‘… it dawned on me a few days ago, perhaps incorrectly, that even the speed of light depends on the geometry of the quantum field that it propagates through, and that field is different on earth than in space, but it is still c relative to the quantum field it traverses.’
The speed of light is slower in glass than in the vacuum, because of the interaction of the the photon with the electromagnetic field quanta inside the block of glass. In this sense, the speed of light depends on the quantum field that it propagates through, as you say. On earth, light interacts with the air it passes through, and slows down.
‘… I reasoned that objects on earth are slightly smaller than they would be in space, and that time is also slightly slower here relative to space as well, because of the quantum field geometry of earth’s mass, which I imagined as a point source at its center of mass.’
I do not follow your reasoning, but you are right that clocks run more slowly at the Earth’s surface than in space (weaker gravitational fields). This is ‘gravitational time dilation’. Linked in to it, as Feynman explains in his Lectures on Physics, is the concept of curvature and excess radius. The Earth’s radius is reduced by (1/3)GM/c^2 = 1.5 mm due to the ‘curvature’ effect of gravitation, while the circumference is unaffected (the contraction only occurs along radial gravitational field lines, not parallel to them). So in this sense, the Earth is contracted in radius slightly causing a distortion to Euclidean geometry, while time is slowed down.
‘I extended these ideas to our galaxy, and surmised that our view of the most far away objects in space may likewise be distorted in time.’
We are seeing distant objects in the past. There is a linkage between distance and time, hence Minkowski’s spacetime concept. The further something is away, the further back in time it appears to be because of the time taken for the light to reach us.
In relativity, a clock or other object moving at high velocity relative to an observer will slow down in its internal motions. So the oscillating electrons which emit light from distant receding stars which are moving away from us at high velocity will slow down, and will emit redshifted light. However, this effect is taken account of in the relativistic Doppler redshift formula used in cosmology.
‘It was just a guess, but it looks like science has concluded that the acceleration is caused by “the exchange of field quanta induce acceleration of charges away from each other”.’
That’s what science suggests because it makes checkable predictions which are confirmed, but it isn’t what mainstream scientists are likely to say. (They are more likely to say that ‘mysterious dark energy’ causes cosmological acceleration, because of ignorance and love of the occult.)
‘..is the speed of light the same no matter where you observe it, or does it change depending on where ..oh..wait, no no no…we can observe atomic clocks on space craft moving slowly, but we will never view light moving from that craft, or anywhere else, as an outside observer, as moving faster or slower than c. It will be c, always. Of course.
‘So, even though physical lengths and time may change, the speed of light is immune from change.’
The speed of light is reduced when it enters a block of glass, ice, perspex, water, air, etc.
The mechanism of restricted relativity is that the measuring instrument gets contracted and slowed down due to its own motion in the quantum gravity field: this means that the observer’s measurements are affected when you try to measure the speed of light. The classic example of this is as follows:
‘The Michelson-Morley experiment has thus failed to detect our motion through the aether, because the effect looked for – the delay of one of the light waves – is exactly compensated by an automatic contraction of the matter forming the apparatus [the Lorentz contraction itself is physically caused by the head-on pressure of the quantum graviton field against the front of the moving particle, squeezing it slightly in the direction of motion] … The great stumbing-block for a philosophy which denies absolute space is the experimental detection of absolute rotation.’
– Professor A.S. Eddington (who confirmed Einstein’s general theory of relativity in 1919), MA, MSc, FRS, Space Time and Gravitation: An Outline of the General Relativity Theory, Cambridge University Press, Cambridge, 1921, pp. 20, 152.
I hope this is helpful!
I did not get it, how do you apply my argument? –Gil
You argue that successful applications of a theory (ST) to other areas than the key areas provides weak support for the original theory!
Applying your argument to classical physics, the much stronger successes of Maxwell’s equations of classical electromagnetism (for instance to thousands of situations in electromagnetism) will make that theory win hands-down over the relatively few things that you can specifically calculate using quantum electrodynamics (magnetic moments of leptons, Lamb shift in hydrogen spectra).
Your argument that you can have support for a theory from indirect successes ignores alternative ideas which do a lot better! E.g., there are alternatives to string theory which do make calculations that are checkable. Your argument specifically gives support to a failed theory of gravity because you are:
(1) not demanding that the failed theory of gravity (ST) require falsifiable predictions
and
(2) ignoring alternative ideas to string. Once you include alternative ideas, ST “successes” are shown to be failures by comparison.
What you are neglecting is that indirect calculational successes are no support for a theory: Ptolemy’s epicycles could enable predictions of apparent planetary motions, but that is not evidence. Model building by the AdS/CFT conjecture is not a falsifiable physics, any more than building theories of epicycles. You need falsifiable predictions of the key elements to the theory, to provide scientific evidence that supports the theory. To hype or defend a theory without even a single falsifiable prediction is appalling:
‘String theory has the remarkable property of predicting gravity.’ – Ed Witten, M-theory originator, Reflections on the Fate of Spacetime, Physics Today, April 1996.
This abuse of science is just the defence made for epicycles, phlogiston, caloric, etc. It just stagnates the entire field by leading to hype of drivel which creates so much noise that the more useful ideas can’t be heard.
“Ptolemy’s epicycles could enable predictions of apparent planetary motions, but that is not evidence.”
This was very nice, no? A giant intellectual and scientific achievement of the time.
(I still did not understand your other argument.)
Hi Gil,
Making predictions from a false mathematical model such as Ptolemy’s earth centred system, which is endlessly adjustable, or ST which relies on unobservables such as extra dimensions, may be useful until a better theory comes along, but it is not scientific! Such predictions are not falsifiable because the model is adjusted when it fails, for example by adding more epicycles to “correct” errors. With ST you can select different brane models, different parameters for the moduli of the Calabi-Yau manifold, etc.
In 250 BC, Aristarchus of Samos had the solar system theory. Ptolemy in 150 AD ridiculed Aristarchus’ solar system, falsely claiming that if it was true, with the earth spinning daily, clouds would be continuously shooting over the equator at 1000 miles/hour, and people would be thrown off by the motion. The problem with a false theory being defended for non-falsifiable applications is that it becomes dogma, leading to unwarranted attacks on more useful ideas.
I don’t agree that it was a giant intellectual and scientific achievement of the time. It was a step backwards from Aristarchus’ earlier solar system theory.
Going back to what you say you do not understand: you claimed that indirect applications of a theory provide weak support for the main theory. I point out that if indirect applications provide weak support as you claim, then direct applications of a theory such as classical theories will by analogy provide relatively strong support for the theory. Since you are ignoring other criteria (like the existence of alternative theories which do a better job) in judging whether ST is deemed to be supported by AdS/CFT and company, it follows from using your way of judging support for a theory, that since classical electromagnetism is relatively strong, classical electromagnetism would win out over QED which has fewer specifically unique predictions. Your argument that indirect applications lend some support to string theory is a big step backwards scientifically. Indirect applications don’t support a theory at all, successful falsifiable predictions of the main claims of the theory are needed to provide any support. Even then, the theory isn’t proved. Your statement on Not Even Wrong supports a retreat from Popper’s criterion of science back to the kind of low standards which accommodate fashionable nonsense, ad hoc modelling that doesn’t lead to progress in fundamental physics, but instead creates a belief system akin to religious groupthink, which becomes dogma and leads to correct alternative ideas being ignored or falsely dismissed.
OK, I see your point of view. You make the analogy between ST and Ptolemy’s earth centered systems. What is the analog of Aristarchus theory then?
Ha ha!
copy of a comment submitted to
http://mattleifer.info/2007/11/05/publishing-online-vs-traditional-academic-publishers/#comment-346
‘My main concern is not money, since most academic books make little or no money for the authors anyway, but prestige. At the moment, having a book published by a reputable academic publisher looks good on your CV and may help with tenure review, promotion and other career advancement. Self-publishing a book on the internet confers no such advantage, so academics are naturally motivated to pursue traditional publication.’
That’s the mediocrity publishing principle: if you don’t have anything really worth writing, get a good publisher so that – if nobody reads it – at least the author can point out that (after it is remaindered) that it was published by a famous publishing house. Very impressive!
Two advantages of internet publication should be that an author should be able to update a publication with the latest research, and by-pass mainstream-biased peer-review. However, that’s easier said than done. I uploaded a paper to CERN document server and now can’t revise it because they prevented revisions in 2004, and of course the purpose of arXiv is not peer-review but support of mainstream ideas as they freely admit:
http://arxiv.org/help/endorsement –
‘We don’t expect you to read the paper in detail, or verify that the work is correct, but you should check that the paper is appropriate for the subject area. You should not endorse the author … if the work is entirely disconnected with current work in the area.’
So the internet media ends up censored (on unscientific grounds, e.g. fashion), just like mainstream print media.
A thing to note about the gravitational force is its progressive transition from equilibrium around the centre of the Universe to a purely radial force for expansion at the periphery, opposed only by inertia as in free fall. Transversely to this direction the force will decline to zero so it cannot be treated as a cosmic constant. The result of this will be a scattering of inert matter into cosmic dust, as the origin of ‘dark matter’ permeating space into which the rest of the Universe expanded. Any radiation intercepted would be instantly dissipated predominantly at black-body wavelengths barely above zero.
You can forget ‘echoes of the Big Bang’ as that would have occurred in total silence and darkness, and even the Big Bang itself as expansion accelerates from a standing start, moderated solely by inertia. In its place we may find a dense mass, in which all energy is latent, but which by virtue of its shape is more unstable at its surface than at its centre. Unable to radiate its heat, a rapid rise in surface temperature creates a multitude of lesser bangs. Only then would gravity in its modern sense begin to appear, with the ability to moderate what could otherwise escalate in a runaway destructive explosion. Instead of that we have an explosion in slow motion which we are still living through billions of years later.
Perhaps not getting on for 14 billion as that assumes a constant speed of light, whereas like the gravitational force it will have built up over time, and for the same reason. It is such assumptions as these on the most basic forces in physics that have allowed a mass of conflicting theories to develop, of which, as Feynman observed, there are many times more than there are demonstrable facts.
The difficulty of maintaining consistency throughout an argument appears in an attempt to ratonalise the value put on the gravitational constant by C.V.Boys when that is based on Newton’s belief in a pull of gravity and includes a geometrical factor that is not appropriate to the case of shadow gravity where even the inverse-square disappears. I illustrate this in quite simple terms on my web page. The situation is compounded by the constant not being universal, but a local empirical factor.