Path integrals

Richard P. Feynman, QED, Penguin, 1990, pp. 55-6, and 84:
‘I would like to put the uncertainty principle in its historical place: when the revolutionary ideas of quantum physics were first coming out, people still tried to understand them in terms of old-fashioned ideas … But at a certain point the old fashioned ideas would begin to fail, so a warning was developed that said, in effect, “Your old-fashioned ideas are no damn good when …”. If you get rid of all the old-fashioned ideas and instead use the ideas that I’m explaining in these lectures – adding arrows [arrows = path phase amplitudes in the path integral, eiS -> cos S, for the real phase component] for all the ways an event can happen – there is no need for an uncertainty principle! … on a small scale, such as inside an atom, the space is so small that there is no main path, no “orbit”; there are all sorts of ways the electron could go, each with an amplitude. The phenomenon of interference [by field quanta] becomes very important …’
“path integrals” is the underlying physical dynamics of paths in 2nd quantization, i.e. the Feynman pictorial interpretation of the ∫exp(iS) dx^n, where S = ∫Ldt. Feynman’s diagrams drop complex space, so this becomes ∫cos S dx^3 which is even simpler when you plot it on a diagram; please see Feynman’s Figure 24 here: https://faculty.washington.edu/seattle/physics441/feynman-QED/qed2.pdf
“Path integral” is really not an integral, but a discrete summation: ∑ cos S, over all paths that can connect the point of path origin to the point of detection. What’s really important for making calculations in QFT is the perturbative expansion’s “propagator”, usually considered the Fourier transform of the Yukawa-Coulomb potential energy, U = [exp(-mr)]/(4πr). In Feynman’s simplified (and physically accurate) “real (non-complex) space path summation” we don’t need the Fourier transform, just the Laplace transform which gives the following “fun” calculation (we evaulate the integral over radial distances 0 to infinity):
propagator, V = ∫U [exp(-kr)] d^3 r
= ∫U [exp(-kr)] (4πr^2) dr
= ∫ { [exp(-mr)]/(4πr) } [exp(-kr)] (4πr^2) dr
= ∫ r [exp{-(k + m)r)] dr
= 1/(k + m)^2 = the “propagator”
And that’s it. To calculate each Feynman diagram’s contribution to the total amplitude, you simply multiply the “propagator” derived above, 1/(k + m)^2, by the number of internal lines in the Feynman diagram, and also multiply the number of vertices by the force coupling constant. The perturbative expansion to the so-called “path integral” (which I’d reformulate as the summation ∫exp(iS) dx^n -> ∑ cos S, following the older not younger version of Feynman) then becomes simple.
There shouldn’t be any calculus in quantum field theory, because the whole point is that you are replacing continuous fields with a series of point interactions. Like pollen fragments undergoing Brownian motion due to air molecule bombardment, the electron is undergoes a series of interactions with Coulomb field quanta (“virtual” photons) which deflect it. A better example of the failure of calculus in the real world of discrete interactions in the 1950s was the fallout speed error from the H-bomb’s 100,000 foot mushroom cloud: calculations with Stokes law and average air viscosity massively underestimates the fallout descent rate of 5 micron diameter particles at such high altitudes. The standard theory of a continuously acting force gives you a “terminal velocity” which doesn’t actually exist: the fallout particle instead plummets like an accelerating apple in a vacuum in free-fall, apart from occasional discrete collisions (impacts) with air molecules in that low-density air. It turns out that the continous (calculus based) approximation is only valid for particles large enough, in air of density high enough, that the rate of interaction between the dust and the air molecules bombardment is high enough to prevent significant acceleration between impacts! There is every reason to think that this kind of error is also applicable to quantum field theory.
There’s a further application of the fallout analogy of use in understanding the path integral, namely Schuert’s method of mapping out – and adding up the contributions to – path integrals for particles falling through a wind shear structure which carries them in different directions and with different speeds at different altitudes, in order to work out the “hot line” of maximum fallout on the ground. This has a certain analogy to the use of path integrals to work out the path of least action:
“There are loads of other “clues”. One massive issue which again is totally ignored by the mainstream (including PW) and by popular science writers is that the quantum electrodynamic propagator has the form: 1/(m + k)^2, where m is the virtual massive (short ranged) electromagnetic field quanta (e.g. the virtual electrons and positrons that contribute vacuum polarization shielding and other effects between IR and UV cutoffs), and k is the term for the massless (infinite range) classical Coulomb field quanta (virtual photons which cause all electromagnetic interactions at energies lower than the IR cutoff, i.e. below collision energies of about 1 MeV, which is the minimum energy needed for pair production of electrons and positrons).”
“The point is, you have two separate contributions to the mass of a particle from such a propagator: k gives you the rest mass, while m gives you additional mass due to the running coupling for collision energy >1MeV. (See for instance fig 1 in https://vixra.org/pdf/1408.0151v1.pdf .)”
“The fact that you can separate the Coulomb propagator’s classical mass of a fermion at low energy (<1 MeV) from the increased mass due to the running coupling at higher energy, proves that there’s a physical mechanism for particle masses in general: the virtual fermions must contribute the increase in mass at high energy by vacuum polarization, which pulls them apart, taking Coulomb field energy and thus shielding the electric charge (the experimentally measured and proved running of the QED coupling with energy). In being polarized the electric field, the virtual positron and electron pair (or muon or tauon or whatever) soaks up real electric field energy E in addition to Heisenberg’s borrowed vacuum energy (h-bar/t). So the virtual particles must have a total energy E + (h-bar/t), which allows them to turn the energy they have have absorbed (in being polarized) into mass. This understanding of the two terms in the propagator, m and k, therefore gives you a very simple mechanism basis for predicting all particle masses, m, which shows how the mass gap originates from treating the propagator as a simple physical model of real phenomena…”
Basically, Woit has a useful clue, but is sailing in the wrong direction due to an elitist bias that fancy mathematics is definitely the right way to go – it helps in some ways but you need to also correct errors in the standard model and in some areas like the path integral, the direction should be away from calculus and towards discrete interactions. We should look at what’s physically occurring and take the perturbative expansion as reality, seeking to relegate calculus to just an approximation for high rates of interactions, but of much use for understanding mechanisms, which are discrete summations, not continuous variables in integrals.
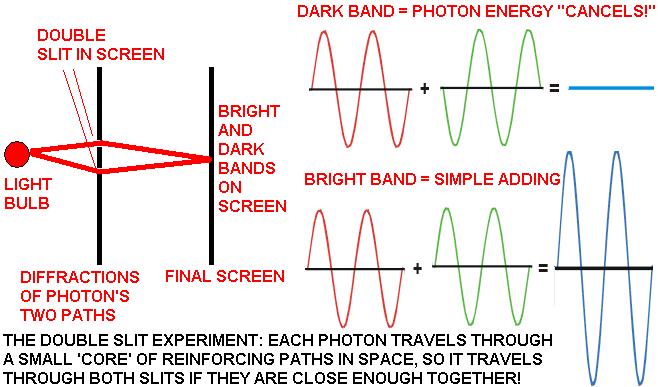
Above: the double slit experiment is as Feynman stated the ‘central paradox of quantum mechanics’. Every single photon gets diffracted by both of two nearby slits in a screen because photon energy doesn’t travel along a single path, but instead, as Feynman states, it travels along multiple paths, most of which normally cancel out to create the illusion that light only travels along the path of least time (where action is minimized), so the double slit and a few other situations are the rare special cases that show up the true nature of light photons as individually traveling along spatially extended paths:
‘Light … uses a small core of nearby space. (In the same way, a mirror has to have enough size to reflect normally: if the mirror is too small for the core of nearby paths, the light scatters in many directions, no matter where you put the mirror.)’ – R. P. Feynman, QED, Penguin, 1990, page 54.
If there are two effective paths that deliver energy to the screen, path 1 and path 2 (as in the double slit experiment with a single photon) then the square of the resultant of the amplitudes for the two paths, A1 and A2, respectively, will be given by |A1 + A2|2, where the squaring the modulus of the sum of the amplitudes is Born’s interpretation of the probability density relationship to the wavefunction. Similarly, in electromagnetism the energy density is proportional to the square of the electric field intensity, which represents a relative wavefunction amplitude for electromagnetic radiation (there’s no mystery to what the “wavefunction” represents for light waves).
Feynman’s genius in discovering path integrals was the amazing intuition it took to realize that Dirac’s ‘propagator’ (derived by Dirac in 1933 from the time-dependent Schroedinger equation’s result for the probability of a path: e–iHT/h-bar where H is the Hamiltonian for a path, i.e. simply the kinetic energy if dealing with a free particle, and T is simply time), namely eiS/h-bar where S is action, could be used to represent each path without the need for squaring the modulus of the amplitude! The complex number in the exponent does it all for you, so you just need to integrate eiS/h-bar for all paths contributing energy that affects the overall amplitude. Hence, the relative probability for any given pair of two paths in the double slit experiment is simply: (|A1 + A2|2) = B|[eiS(1)/h-bar + eiS(2)/h-bar]|2,
where B is a constant of proportionality (easily determined by adding up all paths and normalizing the summation to a total probability of 1, since energy is conserved and the photon definitely ends up somewhere, so the sum of all possible path amplitudes must be equal to a probability of exactly 1 of finding the photon!). Dirac had taken the Hamiltonian amplitude e–iHT/h-bar and derived the more fundamental lagrangian amplitude for action S, i.e. eiS/h-bar. Dirac however restricted his work on this problem to merely the classical action S, whereas Feynman had the genius to extend it to sum over the actions S for all paths, not just the classical action! However notice that this summation over all paths has never, ever, ever been proved to require a summation of any curved paths, where there is no mechanism for such curvature in quantum fields. Curved geodesics in general relativity are merely the results of using differential geometry with a necessarily false smoothed-out source term tensor Tab to deliberately and artificially give rise to a smooth curvature! In place of the factually proved discontinuous distribution of particles of matter and energy (photons, etc.) which give rise to all gravitational fields, the stress-energy-momentum tensor Tab in the field equation of general relativity uses an artifically smoothed-out averaged distribution, with the real world particulate field discontinuities falsely eliminated! E.g., all of the particles of matter and energy are just ignored and replaced by a totally fictitious ‘perfect fluid’ continuum in general relativity: this false source field continuum then gives rise to the equally unphysical curved spacetime continuum because it is equated to the Ricci curvature tensor minus a contraction term for conservation of mass-energy.
So, instead of calculating the gravitational fields from a large number of discontinuous particles, general relativity averages out the mass per unit volume and uses the average, giving rise to a false model of gravity which is only approximately valid for certain conditions where the statistical number of gravitons is large enough to average out and appear like a classical field! General relativity is therefore not ‘only missing’ a vital ingredient (quantum fields), but it is entirely a false framework to start off with because of the mass-energy-momentum tensor which doesn’t describe real particulate gravity-causing fields, but only represents at best artificial approximations to such fields which are roughly applicable for large masses.
Anyone with a knowledge of calculus and more than one brain cell knows that discontinuities cause problems to differential equations; vertical steps produce infinities when differentiated to find gradients! There is actually no mechanism for a smooth curvature of geodesics in quantum field theory, where nobody has ever proved that particles (including virtual particles and cancelled particle paths in path integrals!) don’t travel according to Newton’s 1st law of motion (straight lines in the absence of quantum interactions which impart forces!). Crackpottery is often introduced into mainstream accounts of path integrals by false claims that curved particle paths are ‘permitted’ by the path integral formulation, but that these paths are cancelled out.
This is false, and the reason for it is to introduce false mythology into physics. There is no evidence for it, there is no checkable prediction from it, and it is pseudoscience. It is a lie to claim that physics requires curved paths of particles to be included in path integrals. It doesn’t. See Feynman’s treatment of the refraction of light using graphical illustrations of path integrals (without any equations at all!) in his 1985 book QED: the you don’t need wiggly curved paths to be included. All you need to include are straight line paths from light bulb to the water surface, and then after a discrete deflection at the water surface, another straight line path in the water to the receiver. The differing paths consist solely of straight lines with varying angles of deflection at the water surface! You don’t need to include any curved lines.
Above: Professor Zee lies in Chapter I.2 of his book Quantum field theory in a nutshell (Princeton, 2003) that if the screen with two slits in the double-slit experiment has more and more holes drilled into it so that it eventually disappears altogether, you get chaotic path integrals because – so he falsely claims on page 9 – the photons will still diffract just as if they are going through small slits! Zee is so stupid that he ignores the whole mechanism for diffraction by a slit: the photon interacts with the electromagnetic fields of the electrons in the material along the edge of a slit, and is thus diffracted. When you remove the slits altogether, there are no edges left to cause photons to diffract, so contrary to Zee, photons don’t go loopy in empty space as if they are being diffracted by an infinite number of slits! Think about the refraction of light when entering glass: the electromagnetic fields in the photon interact with those of the electrons in the glass, and the result is a change in the velocity of light, causing refraction of light by glass. The edge of a slit has electrons in it, and the electromagnetic fields of those electrons interact with the nearby photon, causing it to diffract. Drill lots of holes and yes you get more complex interferences, but if you remove the material altogether you suddenly have no edges of slits left to cause diffraction, so the chaos disappears and things become simple!
Not only is he so gullible and mad that Zee ignores this obvious physical mechanism, but he falsely attributes his crank analysis to Feynman, who did not author it! (See Feynman’s book, QED, Princeton, 1985 for the facts Zee ignores!) Zee is just a liar and a fraudster: he is not just a charlatan but he draws a salary from teaching lies to people and he sells books with lies in them, which makes him a quack. Quack science often becomes mainstream: Hitler’s genocide was based on quack genetics, for example. So we need to catch these perpetrators and prosecute them for fraud, and convict them for willful deception for profit. Zee also makes some purely physical errors about particle spins, and promotes them with false propaganda. E.g., his path integral for quantum gravity presupposes spin-2 gravitons and then tries to justify this lie by excluding all the mass in the universe except for two small test masses. Obviously for just two masses, you would indeed need spin-2 graviton exchange to pull them together. But he does not state that if you include all the other masses in the universe (all carry gravitational charge, so there is no way to prevent them from exchanging gravitons with your two little test masses), you don’t need spin-2 gravitons anymore because you can predict gravity with spin-1 gravitons, allowing you to incorporate gravity into the revised Standard Model and have the final theory! But that is just a mistake by Zee, unlike his deception over what Feynman’s path integrals say about the double slit experiment, so it isn’t necessarily a fraud, just plain incompetence which suggests Zee should be sacked from his job for ignorance in the basics of physics. However, I’d like to see Witten kicked out of the Institute of Adcanced Study in Princeton for his massive lie:
‘String theory has the remarkable property of predicting gravity.’ – Dr Edward Witten, M-theory originator, ‘Reflections on the Fate of Spacetime’, Physics Today, April 1996.
This lie damaged my chances of getting my discovery published in Classical and Quantum Gravity, so it has held back scientific progress. I know Witten would possibly argue that my work would have been rejected anyway, but there is such a thing as the straw that breaks the camel’s back; such lies don’t help physics.
In high energy physics above the IR cutoff you get pair production, as explained in detail in the previous post. This causes ‘loops’ in which bosonic field quanta knock pairs of virtual fermions free from the unobservable ground state of the vacuum/ether, which soon annihilate back into radiation again in a ‘loop’ of repeated virtual fermion creation and annihilation. Although it is convenient to depict this process by a circular loop on a spacetime Feynman diagram, even this situation (which is irrelevant below the 1 MeV IR cutoff for all low-energy physics anyway) is not physically composed of curved particle All apparent cases of ‘curvature’ are merely a lot of straight lines joined up with particle interactions occurring at the vertices! Starlight deflected by the sun is deflected in a series of quantum graviton interactions in the vacuum, and the overall result can be statistically modelled to a good approximation by ‘curvature’ but such curvature remains just an approximation. There is no curved continuum spacetime, there is quantum spacetime. This is even clear when you look at the lies needed in general relativity: as soon as you introduce the properly quantized Tab energy-momentum-stress tensor as the source of the gravitational field, the theory falls to pieces because the Ricci tensor only represents a continuously variable curved geodesic, not a straight line with discontinuities.
The whole of general relativity is just a classical approximation that usefully allows calculations to be made (albeit with a loss of physical intuition for the nature of the real world) incorporating the conservation of field energy into classical gravitation. It’s a lie to presume that general relativity, or any theory representing discontinuous fields as continuously variables in differential calculus, is a physically correct model. Such calculations are fairly complex approximations to the awesomely simple nature of the physical world, which doesn’t use the calculus.
With Feynman’s innovation, any problem in quantum mechanics generally can be evaluated by integrating the Dirac propagator over all path actions, thus instead of having to follow Born and add up the squares of the moduli of amplitudes for each path, we just instead add up a linear summation of eiS(n)/h-bar terms, which is much easier and quicker (even a bright two year old can do it without making a mistake on a calculator). There is no mathematics beyond the trick of summing the amplitudes in such a way that they add up in a physically logical simple way without negative probabilities! For large numbers of paths, we can sum using calculus, by integrating eiS(n)/h-bar for an infinite number n of possible geometric paths with differing actions S(n). (This integration may be mathematically hard, and may lead to infinities and problems in some cases, but that’s a human mathematical problem of using the calculus, it’s not a proof that nature is complex! Duh!) Just so that readers who don’t understand quantum field theory can see what we’re doing, S is action: action is the integral of the lagrangian over time, and the lagrangian for a free particle in a field is simply the difference between the kinetic energy, E = (1/2)mv2 for non-relativistic situations, and the potential energy it has from the field it is immersed in. If a free massive particle has no potential energy and only kinetic energy, then the lagrangian is just the kinetic energy, (1/2) mv2. Integrate that over time and the result is the action, S. The amplitude for the path integral just requires the action S and Planck’s constant, h. The bar through h (i.e. h-bar) signifies h divided into twice Pi, a result of the geometry of rotational symmetry. There’s absolutely no complex mathematics whatsoever, no stringiness whatsoever, within nature; instead it is beautifully simple and factual. It’s really important for me to stress that Feynman was not, definitely not, merely trying to solve the problem of the infinite momenta of field quanta at close to the middle of an electron, and other quantum field theory problems with path integrals by imposing cutoffs for infrared and ultraviolet divergences (i.e. renormalization) in his theory. That is a lie, spread by liars in the mainstream who believe in extradimensional crap. Yes, Feynman did solve problems with renormalization, but what is being suppressed is that that his innovation is not a mere abstract addition to the existing theory of quantum mechanics. It’s a revolution which replaces Bohring physics of multiverse speculations and other nonsense with facts, as you can see by reading the key paper by Feynman which was inevitably rejected by the Physical Review (see page 2 of 0004090v1; due to egotistical cranky ‘peer’ reviewers who worship false dogma and abhore factual physics, the Physical Review has regularly acted as a typical pseudoscience propaganda journal which believes that religious lobbying is a substitute for hard facts from experimental work on quantum gravity), before being published in Reviews of Modern Physics, vol. 20 (1948), p. 367:
‘This paper will describe what is essentially a third formulation of nonrelativistic quantum theory [Schroedinger’s wave equation and Heisenberg’s matrix mechanics being the first two attempts, which both generate nonsense ‘interpretations’]. This formulation was suggested by some of Dirac’s remarks concerning the relation of classical action to quantum mechanics. A probability amplitude is associated with an entire motion of a particle as a function of time, rather than simply with a position of the particle at a particular time.
‘The formulation is mathematically equivalent to the more usual formulations. … there are problems for which the new point of view offers a distinct advantage. …’
Wow, what an understatement! I’m not alone in supporting Feynman’s case against the crackpot, backward mainstream which is still stuck in 1927 with obsolete physics and hasn’t grasped path integrals at all. E.g., Richard MacKenzie clearly supports what I’m saying about Feynman where he writes in his paper Path Integral Methods and Applications, pages 2-13:
‘… I believe that path integrals would be a very worthwhile contribution to our understanding of quantum mechanics. Firstly, they provide a physically extremely appealing and intuitive way of viewing quantum mechanics: anyone who can understand Young’s double slit experiment in optics should be able to understand the underlying ideas behind path integrals. Secondly, the classical limit of quantum mechanics can be understood in a particularly clean way via path integrals. … for fixed h-bar, paths near the classical path will on average interfere constructively (small phase difference) whereas for random paths the interference will be on average destructive. … we conclude that if the problem is classical (action >> h-bar), the most important contribution to the path integral comes from the region around the path which extremizes the path integral. In other words, the article’s motion is governed by the principle that the action is stationary. This, of course, is none other than the Principle of Least Action from which the Euler-Lagrange equations of classical mechanics are derived.’
So far so good, but I must point out that MacKenzie goes on to make a terrible error in his analysis of the Aharonov-Bohm effect, where a shielded box containing a magnetic field is placed between the two slits in the double slit experiment, and the photon interference pattern is affected by the magnetic field in the box. (This experiment was first done by Chambers in 1960.) The fatal mainstream error MacKenzie makes is the implicit assumption that the ‘shield’ which eliminates the observable magnetic field actually stops that magnetic field instead of merely cancelling it by superposition! Magnetic fields work by polarization. Little magnets such as fundamental spinning charges align against an external field in such a way as to oppose and partially ‘cancel’ that field: but this cancellation is a superposition of two fields, not the elimination of a field. Think simply: if you put a child on each end of a see-saw, it may balance, but that doesn’t mean you have cancelled out all the forces. You have only cancelled out some of the forces: you have ensured that the forces balance but there is still a force on the fulcrum that isn’t ‘cancelled out’. Similarly, if you have $1000 credit in one bank account and a debt of $1000 in another, you aren’t free from debt unless you transfer the money across.
What happens with magnetic fields is any material is full of magnetic fields because all fundamental particles have have electric charge and spin, but normally the random orientations or the paired up spins (adjacent electrons in an atom are paired with opposite spins under the Pauli exclusion principle) mean that normally the magnetism cancels out. Only when you have an asymmetry, aligning more of the spins one way than the opposite way, do you see the magnetic field. In the absence of alignment, the fields cancel by superposition, but the energy is still there in the field (energy is conserved). Therefore, in the Aharon-Bohm effect, the influence of the ‘shielded’ magnetic field on the interference pattern isn’t ‘magical’ or unexpected. The magnetic fields of the photon are affected by the energy density of the ‘cancelled’ magnetic fields, just as light slows down in a block of glass due to the energy density of the electromagnetic fields from the charged matter making up glass!
All of the mainstream ‘physicists’ (quacks) I’ve spoken to believe wrongly that because an ‘uncharged’ block of glass contains as many protons as electrons and hence has a net electric charge of zero, the electric fields ‘don’t exist’ anymore there, just as they claim the magnetic fields ‘don’t exist’ in the Aharonov-Bohm effect. They are so far gone into mystical eastern entanglement quackery that they they just ignore anomalies and become abusive when disproved time after time, and of course they get still more and more angry when you predict gravity factually and all the related predictions from the corrected physics. They are all totally insane, they are bad losers, they hate real physics, they hate the way the world really is!
This is essential to the checkable aspects of quantum gravity, i.e., low energy quantum gravity stuff like predicting the gravity force coupling parameter G, because at low energy graviton fields will carry a very low energy density (gravity is 1040 times weaker than electromagnetism at low energy, everyday physics). Therefore, at low energy, we can ignore the effects of graviton emission from the energy of the gravitational fields (because they are so weak at low energy) which ensures that the path integrals for quantum gravity will be similar to those of electromagnetism for low energy physics, where the checkable predictions of quantum gravity will be found. Who – apart from nutty string theorists – cares about the uncheckable speculations of Planck scale quantum gravity? If we first get a quantum gravity theory that makes correct checkable predictions at low energy, then we will be in a position to make confident extrapolations from that particular theory to higher energies. We can’t have that confidence if we start with speculations of high energy that can’t be checked! Duh! Get a grip on reality, all you string theorists and fellow-travellers in the media!
This makes quantum gravity path integrals very simple for low energy, like electromagnetism. So let’s deal with electromagnetism first, then move on to quantum gravity.
Feynman’s explains that all light sources radiate photons in all directions, along all paths, but most of those cancel out due to destructive interference. If you throw a stone at an apple, the apple won’t move significantly if someone on the other side of the apple does the same thing with a similar stone! The two impacts will cancel out, apart from a compression of the apple! In other words, there are natural situations where exchange radiation causes destructive interference, and the nature of light is exactly this situation.
The amplitudes of the paths near the classical path reinforce each other because their phase factors, representing the relative amplitude of a particular path, exp(-iHT) = exp(iS) where H is the Hamiltonian (kinetic energy in the case of a free particle), and S is the action for the particular path measured in quantum action units of h-bar (action S is the integral of the Lagrangian field equation over time for a given path).
Because you have to integrate the phase factor exp(iS) over all paths to obtain the resultant overall amplitude, clearly radiation is being exchanged over all paths, but is being cancelled over most of the paths somehow. The phase factor equation models this as interferences without saying physically what process causes the interferences.
Thus, in Feynman’s path integral explanation in his 1985 book QED, an electron when it radiates actually sends out radiation in all directions, along all possible paths, but most of this gets cancelled out because all of the other electrons in the universe around it are doing the same thing, so the radiation just gets exchanged, cancelling out in ‘real’ photon effects. (The electron doesn’t lose energy, because it gains as much by receiving such virtual radiation as it emits, so there is equilibrium). Any “real” photon accompanying this exchange of unobservable (virtual) radiation is then represented by a small core of uncancelled paths, where the phase factors tend to add together instead of cancelling out.
All electrons have centripetal acceleration from spin and so are always radiating, so there is an equilibrium of emission and reception established in the universe, called exchange radiation/vector bosons/gauge bosons, which can only be ’seen’ via force fields they produce; ‘real’ radiation simply occurs when the normally invisible exchange equilibrium gets temporarily upset by the acceleration of a charge.
A conspiracy of mainstream string worshipping physics quacks claims that quantum entanglement exists and that the universe can’t be described in terms of Feynman’s simplicity, but this is a lie as exposed by the following facts:
Editorial policy of the American Physical Society journals (including PRL and PRA):
From: Physical Review A [mailto:pra@aps.org]
Sent: 19 February 2004 19:47
To: ch.thompson1@virgin.net
Subject: To_author AG9055 Thompson
Re: AG9055
Dear Dr. Thompson,
… With regard to local realism, our current policy is summarized succinctly, albeit a bit bluntly, by the following statement from one of our Board members:
“In 1964, John Bell proved that local realistic theories led to an upper bound on correlations between distant events (Bell’s inequality) and that quantum mechanics had predictions that violated that inequality. Ten years later, experimenters started to test in the laboratory the violation of Bell’s inequality (or similar predictions of local realism). No experiment is perfect, and various authors invented ‘loopholes’ such that the experiments were still compatible with local realism. Of course nobody proposed a local realistic theory that would reproduce quantitative predictions of quantum theory (energy levels, transition rates, etc.). This loophole hunting has no interest whatsoever in physics.” …’
‘In some key Bell experiments, including two of the well-known ones by Alain Aspect, 1981-2, it is only after the subtraction of ‘accidentals’ from the coincidence counts that we get violations of Bell tests. The data adjustment, producing increases of up to 60% in the test statistics, has never been adequately justified. Few published experiments give sufficient information for the reader to make a fair assessment. There is a straightforward and well known realist model that fits the unadjusted data very well. In this paper, the logic of this realist model and the reasoning used by experimenters in justification of the data adjustment are discussed. It is concluded that the evidence from all Bell experiments is in urgent need of re-assessment, in the light of all the known ‘loopholes’. Invalid Bell tests have frequently been used, neglecting improved ones derived by Clauser and Horne in 1974. ‘Local causal’ explanations for the observations have been wrongfully neglected.’
After her tragic death from cancer in 2006, her website was preserved, where she wrote in defiance of the Physical Review editor man:
http://freespace.virgin.net/ch.thompson1/EPR_Progress.htm:
‘The story, as you may have realised, is that there is no evidence for any quantum weirdness: quantum entanglement of separated particles just does not happen. This means that the theoretical basis for quantum computing and encryption is null and void. It does not necessarily follow that the research being done under this heading is entirely worthless, but it does mean that the funding for it is being received under false pretences. It is not surprising that the recipients of that funding are on the defensive. I’m afraid they need to find another way to justify their work, and they have not yet picked up the various hints I have tried to give them. There are interesting correlations that they can use. It just happens that they are ordinary ones, not quantum ones, better described using variations of classical theory than quantum optics.
‘Why do I seem to be almost alone telling this tale? There are in fact many others who know the same basic facts about those Bell test loopholes, though perhaps very few who have even tried to understand the real correlations that are at work in the PDC experiments. I am almost alone because, I strongly suspect, nobody employed in the establishment dares openly to challenge entanglement, for fear of damaging not only his own career but those of his friends.’
The stringy mainstream still ignores Feynman’s path integrals as being a reformulation of QM (a third option), seeing them instead as QFT: Feynman’s paper ‘Space-Time Approach to Non-Relativistic Quantum Mechanics’, Reviews of Modern Physics, volume 20, page 367 (1948), makes it clear that his path integrals are a reformulation of quantum mechanics which gets rid of the uncertainty principle and all the pseudoscience it brings with it.
Richard P. Feynman, QED, Penguin, 1990, pp. 55-6, and 84:
‘I would like to put the uncertainty principle in its historical place: when the revolutionary ideas of quantum physics were first coming out, people still tried to understand them in terms of old-fashioned ideas … But at a certain point the old fashioned ideas would begin to fail, so a warning was developed that said, in effect, “Your old-fashioned ideas are no damn good when …”. If you get rid of all the old-fashioned ideas and instead use the ideas that I’m explaining in these lectures – adding arrows [arrows = path phase amplitudes in the path integral, i.e. eiS(n)/h-bar] for all the ways an event can happen – there is no need for an uncertainty principle! … on a small scale, such as inside an atom, the space is so small that there is no main path, no “orbit”; there are all sorts of ways the electron could go, each with an amplitude. The phenomenon of interference [by field quanta] becomes very important …’
So classical and quantum field theories differ due to the physical exchange of field quanta between charges. This exchange of discrete virtual quanta causes chaotic interferences to individual fundamental charges in strong force fields. Field quanta induce Brownian-type motion of individual electrons inside atoms, but this does not arise for very large charges (many electrons in a big, macroscopic object), because statistically the virtual field quanta avert randomness in such cases by averaging out. If the average rate of exchange of field quanta is N quanta per second, then the random standard deviation is 100/N1/2 percent. Hence the statistics prove that the bigger the rate of field quanta exchange, the smaller the amount of chaotic variation. For large numbers of field quanta resulting in forces over long distances and for large charges like charged metal spheres in a laboratory, the rate at which charges exchange field quanta with one another is so high that the Brownian motion resulting to individual electrons from chaotic exchange gets statistically cancelled out, so we see a smooth net force and classical physics is accurate to an extremely good approximation.
Thus, chaos on small scales has a provably beautiful simple physical mechanism and mathematical model behind it: path integrals with phase amplitudes for every path. This is analogous to the Brownian motion of individual 500 m/sec air molecules striking dust particles which creates chaotic motion due to the randomness of air pressure on small scales, while a ship with a large sail is blown steadily by averaging out the chaotic impacts of immense numbers of air molecule impacts per second. So nature is extremely simple: there is no evidence for the mainstream ‘uncertainty principle’-based metaphysical selection of parallel universes upon wavefunction collapse. (Stringers love metaphysics.) Dr Thomas Love, who writes comments at Dr Woit’s Not Even Wrong blog sometimes, kindly emailed me a preprint explaining:
‘The quantum collapse [in the mainstream interpretation of quantum mechanics, where a wavefunction collapse occurs whenever a measurement of a particle is made] occurs when we model the wave moving according to Schroedinger (time-dependent) and then, suddenly at the time of interaction we require it to be in an eigenstate and hence to also be a solution of Schroedinger (time-independent). The collapse of the wave function is due to a discontinuity in the equations used to model the physics, it is not inherent in the physics.’
‘… nature has a simplicity and therefore a great beauty.’
– Richard P. Feynman (The Character of Physical law, p. 173)
The double slit experiment, Feynman explains, proves that light uses a small core of space where the phase amplitudes for paths add together instead of cancelling out, so if that core overlaps two nearby slits the photon diffracts through both the slits:
‘Light … uses a small core of nearby space. (In the same way, a mirror has to have enough size to reflect normally: if the mirror is too small for the core of nearby paths, the light scatters in many directions, no matter where you put the mirror.)’
– R. P. Feynman, QED, Penguin, 1990, page 54.
Hence nature is very simple, with no need for the wavefunction collapse or the ‘multiverse’ lie of crackpot Hugh Everett III who wouldn’t even incorporate the physical dynamics of fallout particle sizes and deposition phenomena in his purely statistical paper allegedly predicting fallout casualties:
‘It always bothers me that, according to the laws as we understand them today, it takes a computing machine an infinite number of logical operations to figure out what goes on in no matter how tiny a region of space, and no matter how tiny a region of time. How can all that be going on in that tiny space? Why should it take an infinite amount of logic to figure out what one tiny piece of spacetime is going to do? So I have often made the hypothesis that ultimately physics will not require a mathematical statement, that in the end the machinery will be revealed, and the laws will turn out to be simple, like the chequer board with all its apparent complexities.’
– R. P. Feynman, The Character of Physical Law, November 1964 Cornell Lectures, broadcast and published in 1965 by BBC, pp. 57-8.
Path integrals for fundamental forces in quantum field theory
Richard P. Feynman’s paper ‘Space-Time Approach to Non-Relativistic Quantum Mechanics’, Reviews of Modern Physics, volume 20, page 367 (1948), despite being rejected previously by the Physical Review, is an essential piece of reading. Feynman makes it clear that his path integrals are a reformulation of quantum mechanics, not merely an extension to sweep away infinities in quantum field theory!
Feynman’s model treats the statistical randomness of particle physics by summing all possible paths a particle can take in any interaction (real particles as well as virtual particles such as force-mediating gauge bosons) while assigning a weighting (amplitude) to each path by means of a phase amplitude which can vary for different paths: paths lying near the classical path reinforce automatically while those far from the classical path suffer interference and cancellation.
‘Light … ‘smells’ the neighboring paths around it, and uses a small core of nearby space. (In the same way, a mirror has to have enough size to reflect normally: if the mirror is too small for the core of nearby paths, the light scatters in many directions, no matter where you put the mirror.)’ – R. P. Feynman, QED, Penguin, 1990, page 54.
‘When we look at photons on a large scale … there are enough paths around the path of minimum time to reinforce each other, and enough other paths to cancel each other out. But when the space through which a photon moves becomes too small (such as the tiny holes in the screen), these [classical] rules fail – we discover that light doesn’t have to go in straight lines, there are interferences created by two holes … The same situation exists with electrons: when seen on a large scale, they travel like particles, on definite paths. But on a small scale, such as inside an atom, the space is so small that there is no main path, no ‘orbit’; there are all sorts of ways the electron could go, each with an amplitude. The phenomenon of interference [on small distance scales due to individual field quanta interactions not occurring in sufficiently large numbers to cancel out random chaos, and due to interactions with the pair-production of virtual fermions in the very strong electric fields on small distance scales, where the fields exceed the 1.3*1018 v/m Schwinger threshold electric field strength for pair-production] becomes very important, and we have to sum the arrows to predict where an electron is likely to be.’
– R. P. Feynman, QED, Penguin, 1990, page 84-5.
‘… the ‘inexorable laws of physics’ … were never really there … Newton could not predict the behaviour of three balls … In retrospect we can see that the determinism of pre-quantum physics kept itself from ideological bankruptcy only by keeping the three balls of the pawnbroker apart.’
– Dr Tim Poston and Dr Ian Stewart, ‘Rubber Sheet Physics’, Analog: Science Fiction/Science Fact, Vol. C1, No. 129, Davis Publications, New York, November 1981.
Feynman’s point is that Heisenberg’s uncertainty principle arises from interference between paths a particle can take when virtual particles affect the motion of real particles, and this is very important:
‘I would like to put the uncertainty principle in its historical place: when the revolutionary ideas of quantum physics were first coming out, people still tried to understand them in terms of old-fashioned ideas … But at a certain point the old fashioned ideas would begin to fail, so a warning was developed that said, in effect, “Your old-fashioned ideas are no damn good when …” If you get rid of all the old-fashioned ideas and instead use the ideas that I’m explaining in these lectures – adding arrows [phase amplitudes] for all the ways an event can happen – there is no need for an uncertainty principle!’
– Richard P. Feynman, QED, Penguin, 1990, pp. 55-6.
The uncertainty principle of quantum mechanics itself arises because of interference due to virtual particles.
Feynman is simply adopting Popper’s explanation of the uncertainty principle in this case:
‘… the Heisenberg formulae can be most naturally interpreted as statistical scatter relations [between virtual particles in the quantum foam vacuum and real electrons, etc.], as I proposed [in the 1934 book The Logic of Scientific Discovery]. … There is, therefore, no reason whatever to accept either Heisenberg’s or Bohr’s subjectivist interpretation …’
– Sir Karl R. Popper, Objective Knowledge, Oxford University Press, 1979, p. 303.
(Popper in 1982 added: ‘… the view of the status of quantum mechanics which Bohr and Heisenberg defended – was, quite simply, that quantum mechanics was the last, the final, the never-to-be-surpassed revolution in physics … physics has reached the end of the road.’ – Sir Karl Popper, Quantum Theory and the Schism in Physics, Rowman and Littlefield, NJ, 1982, p. 6. Bohr had been condemned in a letter he received from Rutherford about the Bohr atom, which asked Bohr to explain why the spinning and orbiting electron didn’t radiate and spiral into the nucleus! The true explanation is that in the ground state, the electron receives as much energy from the quantum field vacuum as it radiates, but Bohr didn’t know that so he invented a metaphysical ‘correspondence principle’ and a metaphysical ‘complementarity principle’ which together formed the basis for the 1927 Solvay ‘Copenhagen Interpretation’ of quantum mechanics, which denies that progress in quantum mechanics is impossible, even in principle. Heisenberg sided with Bohr at Solvay in 1927 because his own ‘uncertainty principle’-based matrix mathematics version of quantum mechanics was also physically empty at that time.)
If you subtracted all virtual particle effects from quantum field theory, nothing would be left of physics because all forces are caused by the exchange of virtual particles between real particles. It is because this exchange is chaotic in nature that the Coulomb law is chaotic when dealing with individual charges like individual electrons in an atom. When dealing with large numbers of electrons, the chaotic randomness of individual field quanta exchanges disappears because statistically, with increasingly large numbers of interactions, the situation becomes ever less chaotic and ever more classical in nature. An analogy to this is Brownian motion of small dust particles due to individual impacts from air molecules. Such small dust particles move around chaotically, but larger objects like a ship’s sail experience such a large flux of air molecule interactions that the chaos cancels out and the sail is subject to effectively steadier pressure.
In his lecture ‘This Unscientific Age’, which Feynman gave as part of a series of three lectures under the collective title ‘The Meaning of It All’ in April of 1963 at the University of Washington, he used heavy sarcasm when he rejected outright the concept that probabilities have any physical significance by themselves (probabilities merely quantify the ignorance of human observers):
‘For example, I had the most remarkable experience this evening. While coming in here, I saw licence plate ANZ 912. Calculate for me, please, the odds that of all the licence plates in the state of Washington I should happen to see ANZ 912.’ – Richard P. Feynman, The Meaning of It All, Penguin, London, 1998, p. 81.
Feynman goes on to stress that probabilities are fiction after the event, when we know whether the event occurred or not. The whole concept of probability has nothing to do with reality itself, and is merely an attempt to quantify the ignorance of reality held by some observer. He gives an example in the lecture of a scientist who noticed that a rat took alternative left and right turns while running through a maze and asked Feynman to calculate the remarkably low probability of the event. Feynman replied: ‘… it doesn’t make sense to calculate after the event … you selected the peculiar case. … do another experiment all over again and then see if they alternate. He did, and it didn’t work.’ But people (not just scientists) generally abuse probability theory by calculating pseudo-probabilities after an event has occurred!
Something happens and people like to say it is a one-in-a-million chance, and must therefore have a deep spiritual or metaphysical meaning. In reality, you can calculate such low probabilities for any mundane event, like seeing a particular random plate out of millions at random. Who cares that when you look for number plates and see one, there is just one in a million or less chance that you could have predicted which one you would see in advance? Even when there is statistical evidence that some chance event shows a real correlation between two different things, that doesn’t prove any obvious link between those two things: the classic example is in the book How to Lie with Statistics which reports a definite correlation between the number of storks nests on house roofs in Holland and the number of children in the family of the householder! (This correlation was true, but it didn’t prove the myth that storks deliver babies to families: bigger families simply tended to buy big old houses, which because of their size and age on average had more storks nests on the roof than the typically smaller, newer houses of families with fewer children!)
‘The quantum collapse [in the mainstream interpretation of of quantum mechanics, which has wavefunction collapse occur when a measurement is made] occurs when we model the wave moving according to Schroedinger (time-dependent) and then, suddenly at the time of interaction we require it to be in an eigenstate and hence to also be a solution of Schroedinger (time-independent). The collapse of the wave function is due to a discontinuity in the equations used to model the physics, it is not inherent in the physics.’
– Dr Thomas Love, Departments of Physics and Mathematics, California State University, ‘Towards an Einsteinian Quantum Theory’, preprint emailed to me.
Dr Love points out that the mainstream ‘wavefunction collapse’ Copenhagen interpretation (and all entanglement interpretations) are speculative. He points out that the wavefunction doesn’t physically collapse. There are two mathematical models, the time-dependent Schroedinger equation and the time-independent Schroedinger equation.
Taking a measurement means that, in effect, you switch between which equations you are using to model the electron. It is the switch over in mathematical models which creates the discontinuity in your knowledge. When you take a measurement on the electron’s spin state, for example, the electron is not in a superimposition of two spin states before the measurement. (You merely have to assume that each possibility is a valid probabilistic interpretation, before you take a measurement to check.)
Suppose someone flips a coin and sees which side is up when it lands, but doesn’t tell you. You have to assume that the coin is 50% likely heads up, and 50% likely to be tails up. So, to you, it is like the electron’s spin before you measure it. When the person shows you the coin, you see what state the coin is really in. This changes your knowledge from a superposition of two equally likely possibilities, to reality.
Dr Love states on page 9 of his preprint paper Towards an Einsteinian Quantum Theory: ‘The problem is that quantum mechanics is mathematically inconsistent…’, and compares the two versions of the Schroedinger equation on page 10. The time independent and time-dependent versions disagree and this disagreement nullifies the principle of superposition and consequently the concept of wavefunction collapse being precipitated by the act of making a measurement. The failure of superposition discredits the usual interpretation of the EPR experiment as proving quantum entanglement. In fact, making a measurement always interferes with the system being measured (by recoil from firing light photons or other probes at the object), but that is not justification for the metaphysical belief in wavefunction collapse.
This path integrals formulation is a new theory of quantum mechanics, being an alternative to the mainstream Schroedinger wave description and the Heisenberg’s abstract matrix mechanics. Feynman writes in his 1948 paper:
‘In quantum mechanics the probability of an event which can happen in several different ways is the absolute square of a sum of complex contributions, one from each alternative way. The probability that a particle will be found to have a path x(t) lying somewhere within a region of space time is the square of a sum of contributions, one from each path in the region. The contribution from a single path is postulated to be an exponential whose (imaginary) phase is the classical action (in units of h-bar) for the path in question. The total contribution from all paths reaching x, t from the past is the wave function {Psi}(x, t). …
‘It is a curious historical fact that modern quantum mechanics began with two quite different mathematical formulations: the differential equation of Schroedinger, and the matrix algebra of Heisenberg. The two, apparently dissimilar approaches, were proved to be mathematically equivalent. …
‘This paper will describe what is essentially a third formulation of nonrelativistic quantum theory. This formulation was suggested by some of Dirac’s remarks concerning the relation of classical action to quantum mechanics. A probability amplitude is associated with an entire motion of a particle as a function of time, rather than simply with a position of the particle at a particular time.
‘The formulation is mathematically equivalent to the more usual formulations. There are, therefore, no fundamentally new results. However, there is a pleasure in recognizing old things from a new point of view. Also, there are problems for which the new point of view offers a distinct advantage. …’
Feynman goes on in the paper to obtain his theory from just two postulates, the first being Born’s familiar rule from quantum mechanics (i.e., that the probability of an event is proportional to the square of the wavefunction amplitude), while the second postulate tells you how to calculate the wavefunction contribution from each path:
‘I. If an ideal measurement is performed, to determine whether a particle has a path lying in a region of space-time, then the probability that the result will be affirmative is the absolute square of a sum of complex contributions, one from each path in the region. …
‘II. The paths contribute equally in magnitude, but the phase of their contribution is the classical action (in units of h-bar); i.e., the time integral of the Lagrangian taken along the path.’
Feynman states in a footnote:
‘Throughout this paper the term “action” will be used for the time integral of the Lagrangian along a path. When this path is the one actually taken by a particle, moving classically, the integral should more properly be called Hamilton’s first principle function.’
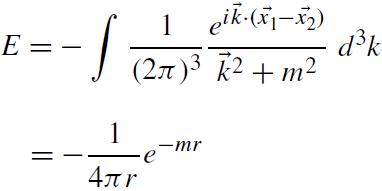
Above: the path integral performed for the Yukawa field, the simplest system in which the exchange of massive virtual pions between two nucleons causes an attractive force. Virtual pions will exist all around nucleons out to a short range, and if two nucleons get close enough for their virtual pion fields to overlap, they will be attracted together. This is a little like Lesage’s idea where massive particles push charges together over a short range (the range being limited by the diffusion of the massive particles into the ‘shadowing’ regions). (See page 26 of Zee for discussion, and page 29 for integration technique. But we will discuss the components of this and other path integrals in detail below.) Zee comments on the result above on page 26: “This energy is negative! The presence of two … sources, at x1 and x2, has lowered the energy. In other words, two sources attract each other by virtue of their coupling to the field … We have derived our first physical result in quantum field theory.” This 1935 Yukawa theory explains the strong nuclear attraction between nucleons in a nucleus by predicting that the exchange of pions (discovered later with the mass Yukawa predicted) would overcome the electrostatic repulsion between the protons, which would otherwise blow the nucleus apart.
But the way the mathematical Yukawa theory has been generalized to electromagnetism and gravity is the basic flaw in today’s quantum field theory: to analyze the force between two charges, located at positions in space x1 and x2, the path integral is done including only those two charges, and just ignoring the vast number of charges in the rest of the universe which – for infinite range inverse-square law forces – are also exchanging virtual gauge bosons with x1 and x2!
A potential energy which varies inversely with distance implies a force which varies as the inverse-square law of distance, because work energy W = Fr, where force F acts over distance r, hence F = W/r, and since energy W is inversely proportional to r, we get F ~ 1/r2. (Distances x in the integrand result in the radial distance r in the result for potential energy above.) In the case of gravity and electromagnetism, the effective mass of the gauge boson in this equation m ~ 0, which gets rid of the exponential term (spin-2 gravitons are supposed to have mass to enable graviton-graviton interactions to enhance the strength of the graviton interaction at high energy in strong fields enough to “unify” the strength of gravity with standard model forces near the Planck scale – an assumption about “unification” which is physically in error (see Figures 1 and 2 in the blog post https://nige.wordpress.com/2007/07/17/energy-conservation-in-the-standard-model/) – and additionally, we’ve shown why spin-2 gravitons are based on error and anyway in the standard model all mass arises from an external vacuum “Higgs” field and is not intrinsic). The exponential term is however important in the short-range weak and strong interactions. Weak gauge bosons are supposed to get their mass from some vacuum (Higgs) field, while massless gluons cause a pion-mediated attraction of nucleons, where the pions have mass so the effective field theory for nuclear physics is of the Yukawa sort.
A path integral calculates the amplitude for an interaction which can occur by a variety of different possible paths through spacetime. The numerator of the path integral integrand above is derived from the phase factor, representing the relative amplitude of a particular path, is simply the exponential term e–iHT = eiS where H is the Hamiltonian (which for the free-particle of mass m is simply representing kinetic energy of the particle, H = E = p2/(2m) = (1/2)mv2; in the event of there being a force-field present, the Hamiltonian must subtract the potential energy V, due to the force field, from the kinetic energy: H = p2/(2m) – V), T is time, and S is the action for the particular path measured in quantum action units of h-bar (the action S is the integral of the Lagrangian field equation over time for a particular path, S = òL dt).
The origin of the phase factor for the amplitude of a particular path, e–iHT, is simply the time-dependent Schroedinger equation of quantum mechanics: i{h-bar}d{Psi}/dt = H, where H is the Hamiltonian (energy operator). Solving this gives wavefunction amplitude, {Psi} = e–iHT/h-bar, or simply e–iHT if we express HT in units of h-bar. Behind the mathematical symbolism, it’s extremely simple physics, just being a description of the way that waves can reinforce if in phase and adding together, or cancel out if they are out of phase.
The denominator of the path integral integrand above is derived from the propagator, D(x), which Zee on page 23 describes as being: ‘the amplitude for a disturbance in the field to propagate from the origin to x.’ This amplitude for calculating a fundamental force using a path integral is constructed using Feynman’s basic rules for conservation of momentum (see page 53 of Zee’s 2003 QFT textbook).
1. Draw the Feynman diagram for the basic process, e.g. a simple tree diagram for Møller scattering of electrons via the exchange of virtual photons.
2. Label each internal line in the diagram with a momentum k and associate it with the propagator i/(k2 – m2 + ie). (Note that when k2 = m2, momentum k is “on shell” and is the momentum of a real, long-lived particle, but k can also take many values which are “off shell” and these represent “virtual particles” which are only indirectly observable from the forces they produce. Also note that ie is infinitesimal and can be dropped where k2 – m2 is positive, see Zee page 26.)
3. Associate each interaction vertex with the appropriate coupling constant for the type of fundamental interaction (electromagnetic, weak, gravitational, etc.) involved, and set the sum of the momentum going into that vertex equal to the sum of the momentum going out of that vertex.
4. Integrate the momentum associated with internal lines over the measure d4k/(2p)4.
Clearly, this kind of procedure is feasible when a few charges are considered, but is not feasible at step 1 when you have to include all the charges in the universe! The Feynman diagram would be way too complicated if trying to include 1080 charges, which is precisely why we have used geometry to simplify the graviton exchange path integral when including all the charges in the universe.
Zee gives some interesting physical descriptions of the way that forces are mediated by the exchange of virtual photons (which seem to interact in some respects like real photons scattering off charges to impart forces, or being created at a charge, propagating to another charge, being annihilated on absorption by that charge, with a fresh gauge boson then being created and propagating back to the first charge again) on pages 20, 24 and 27:
“Somewhere in space, at some instant in time, we would like to create a particle, watch it propagate for a while, then annihilate it somewhere else in space, at some later instant in time. In other words, we want to create a source and a sink (sometimes referred to collectively as sources) at which particles can be created and annihilated.” (Page 20.)
“We thus interpret the physics contained in our simple field theory as follows: In region 1 in spacetime there exists a source that sends out a ‘disturbance in the field’, which is later absorbed by a sink in region 2 in spacetime. Experimentalists choose to call this disturbance in the field a particle of mass m.” (Page 24.)
“That the exchange of a particle can produce a force was one of the most profound conceptual advances in physics. We now associate a particle with each of the known forces: for example, the [virtual, 4-polarizations] photon with the electromagnetic force, and the graviton with the gravitational force; the former is experimentally well established [virtual photons push measurably nearby metal plates together in the Casimir effect] and the latter, while it has not yet been detected experimentally, hardly anyone doubts its existence. We … can already answer a question smart high school students often ask: Why do Newton’s gravitational force and Coulomb’s electric force both obey the 1/r2 law?
“We see from [E = -(e–mr)/(4pr)] that if the mass m of the mediating particle vanishes, the force produced will obey the 1/r2 law.” (Page 27.)
The problem with this last claim Zee makes is that mainstream spin-2 gravitons are supposed to have mass, so gravity would have a limited range, but this is a trivial point in comparison to the errors already discussed in mainstream (spin-2 graviton) approaches to quantum gravity. Zee in the next chapter, Chapter I.5 “Coulomb and Newton: Repulsion and Attraction”, gives a slightly more rigorous formulation of the mainstream quantum field theory for electromagnetic and gravitational forces, which is worth study. It makes the same basic error as the 1935 Yukawa theory, in treating the path integral of gauge bosons between only the particles upon which the forces appear to act, thus inaccurately ignoring all the other particles in the universe which are also contributing virtual particles to the interaction!
Because of the involvement of mass with the propagator, Zee uses a trick from Sidney Coleman where you work through the electromagnetic force calculation using a photon mass m and then set m = 0 at the end, to simplify the calculation (to avoid dealing with gauge invariance). Zee then points out that the electromagnetic Lagrangian density L = -(1/4)FmnFmn (where Fmn = 2dAmn = dmAn – dnAm, Am(x) being the vector potential) has an overall minus sign in the Lagrangian so that action is lost when there is a variation in time! Doing the path integral with this negative Lagrangian (with a small mass added to the photon to make the field theory work) results in a positive sign for the potential energy between two lumps of similar charge, so: “The electromagnetic force between like charges is repulsive!” (Zee, page 31.)
This is quite impressive and tells us that the quantum field theory gives the right result without fiddling in this repulsion case: two similar electric charges exchange gauge bosons in a relatively simple way with one another, and this process, akin to people firing objects at one another, causes them to repel (if someone fires something at you, they are forced away from you by the recoil and you are knocked away from them when you are hit, so you are both forced apart!). Notice that such exchanged virtual photons must be stopped (or shielded) by charges in order to impart momentum and produce forces! Therefore, there must be an interaction cross-section for charges to physically absorb (or scatter back) virtual photons, and this fact offers a simple alternative formulation of the Coulomb force quantum field theory using geometry instead of path integrals!
Zee then goes on to gravitation, where the problem – from his perspective – is how to get the opposite result for two similar-sign gravitational charges than you get for similar electric charges (attraction of similar charges, not repulsion!). By ignoring the fact that the rest of the mass in the universe is of like charge to his two little lumps of energy, and so is contributing gravitons to the interaction, Zee makes the mainstream error of having to postulate a spin-2 graviton for exchange between his two masses (in a non-existent, imaginary empty universe!) just as Fierz and Pauli had suggested back in 1939.
At this point, Zee goes into fantasy physics, with a spin-2 graviton having 5 polarizations being exchanged between masses to produce an always attractive force between two masses, ignoring the rest of the mass in the universe.
It’s quite wrong of him to state on page 34 that because a spin-2 graviton Lagrangian results in universal attraction for a totally false, misleading path integral of graviton exchange between merely two masses, “we see that while like [electric] charges repel, masses [gravitational charges] attract.” This is wrong because even neglecting the error I’ve pointed out of ignoring gravitational charges (masses) all around us in the universe, Zee has got himself into a catch 22 or circular argument: he first assumes the spin-2 graviton to start off with, then claims that because it would cause attraction in his totally unreal (empty apart from two test masses) universe, he has explained why masses attract. However, the only reason why he assumes a spin-2 graviton to start off with is because that gives the desired properties in the false calculation! It isn’t an explanation. If you assume something (without any physical evidence, such as observation of spin-2 gravitons) just because you already know it does something in a particular calculation, you haven’t explained anything by then giving that calculation which merely is the basis for the assumption you are making! (By analogy, you can’t pull yourself up in the air by tugging at your bootstraps.)
This perversion of physical understanding gets worse. On page 35, Zee states:
“It is difficult to overstate the importance (not to speak of the beauty) of what we have learned: The exchange of a spin 0 particle produces an attractive force, of a spin 1 particle produces a repulsive force, and of a spin 2 particle an attractive force, realized in the hadronic strong interaction, the electromagnetic interaction, and the gravitational interaction, respectively.”
Notice the creepy way that the spin-2 graviton – completely unobserved in nature – is steadily promoted in stature as Zee goes through the book, ending up the foundation stone of mainstream physics, string theory:
‘String theory has the remarkable property of predicting [spin-2] gravity.’ – Professor Edward Witten (M-theory originator), ‘Reflections on the Fate of Spacetime’, Physics Today, April 1996.
“For the last eighteen years particle theory has been dominated by a single approach to the unification of the Standard Model interactions and quantum gravity. This line of thought has hardened into a new orthodoxy … It is a striking fact that there is absolutely no evidence whatsoever for this complex and unattractive conjectural theory. There is not even a serious proposal for what the dynamics of the fundamental ‘M-theory’ is supposed to be or any reason at all to believe that its dynamics would produce a vacuum state with the desired properties. The sole argument generally given to justify this picture of the world is that perturbative string theories have a massless spin two mode and thus could provide an explanation of gravity, if one ever managed to find an underlying theory for which perturbative string theory is the perturbative expansion.” [Emphasis added.]
– Dr Peter Woit, http://arxiv.org/abs/hep-th/0206135, page 52.
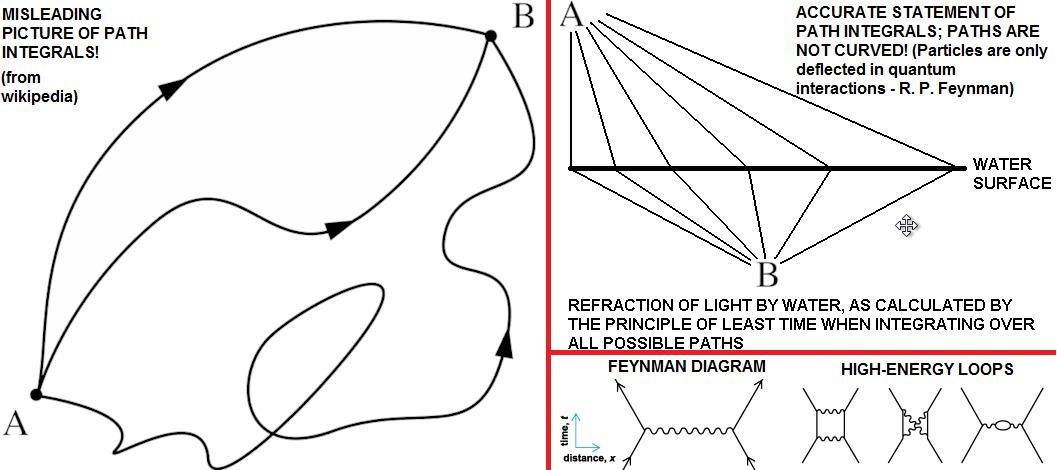
Fig. 1: this illustration makes clear the obfuscation of path integrals given by the mainstream (left side illustration showing curved path histories from location A to location, as shown in Wikipedia’s ‘Path integral formulation’ article) and the true summing of path histories (right side illustration, based on Richard P. Feynman’s 1985 book, QED, showing that there are two things being summed over physically: firstly all the geometric interaction graphs for a single particular type of Feynman interaction diagram to be implemented physically over all geometric possibilities, weighted for interferences, and secondly, a wide range of different Feynman diagrams: this is why the path integral contains an integral for determining the least action such as the minimum force or the least time, as well as being an integral over all kinds of Feynman diagrams).
In classical theories like general relativity, there are no quantum (discrete) interactions being modelled, so the effect of lots of discrete deflections of a photon by gravitons must be represented by a curved line. This is not the true picture. Once you get rid of classical theories altogether, all curvatures are composed of a lot of little deflections due to discrete (quantized) interactions. Inbetween interactions, Newton’s 1st law of motion determines the path of the particle (be it a real particle or a virtual one): it goes in a straight line. There is no curvature. TLike bad textbooks, the Wikipedia article falsely claims:
“In calculating the amplitude for a single particle to go from one place to another in a given time, it would be correct to include histories in which the particle describes elaborate curlicues, histories in which the particle shoots off into outer space and flies back again, and so forth.” [Emphasis added.]
This false belief is also given in many books about path integrals. It is false because, in a true quantum field theory, the whole point is that all accelerations are due to the summation of many little field quanta interactions (e.g. graviton exchange interactions), not a curved spacetime, which is just an approximation for large numbers of interactions! It’s incorrect to include curvature in a quantum field theory, except where the curvature is really a lot of little discrete steps (straight lines joined by vertices where interactions with gravitons or whatever occur). In a quantum field theory, all accelerating motion is composed of lots of discrete interactions such as gauge bosons exchanged (scattered between) charges, as depicted by the following Feynman diagrams:
Fig. 2: Feynman diagrams for classical general relativity and for two different graviton spins.
Similarly, the vast number of impacts of air molecules on the sail when windsurfing gives what approximates to a continuous, smooth force; but it’s due to large numbers (reduce the size of the sail to 5 microns across, and it will move in a completely non-classical, chaotic way due to successive random individual impacts of air molecules, a process called Brownian motion).
One way that some paths could appear to be chaotic and not straight lines is if loops appear along them (bottom of right hand side of Fig. 1 illustration above). Loops are the process of bosonic radiation transforming into pairs of virtual fermions of opposite charge which exist for a brief period and cause effects (like becoming polarized in the field which creates them, and therefore shielding that field slightly by absorbing energy from it, and causing the deflection of moving particles which encounter them) before annihilating back into bosonic radiation. However, this doesn’t cause curvature, it just causes zig-zag deflections in path trajectories, with each vertex corresponding to an interaction with virtual fermions. This doesn’t occur in any case in weak fields, because Schwinger proved that in a steady electric field you need a field strength exceeding 1.3*10^18 volts/metre in order to get pair-production and annihilation (loops). Below that immense field strength, there are no loops.
For this reason, when you apply path integrals for most purposes like low-energy physics (understanding the quantum field theory for gravity and electromagnetism in everyday situations, for example), the paths are always straight lines between quantum interactions due to Newton’s 1st law of motion, as Feynman shows in his book QED. In low-energy physics, you’re summing a lot of simple straight line interaction histories, with the only complexity being that the vertex for the interaction can occur in various possible places in spatial geometry.
E.g., in the Fig. 1 diagram above, the light ray gets deflected – by a quantum interaction – at the water surface, and because the water surface extends over a region of space, this means that you have to take account of the light ray interacting at any location on that water surface. Weighting each interaction path according to the principle of least action (least time in this situation) and integrating them tells you the effective path taken, which is the path that takes the least time to complete. Generally nature is thrifty: this is the principle of least action. When light travels through a path containing air and water (it travels slower through water than air), it appears to take the quickest route possible. This gives the refraction of light by water. Feynman’s while analysis was inspired by the simple question: how does the photon know in advance of reaching the water surface, the best direction to go in order to minimise the time taken? It doesn’t, as Feynman explains: it tries to take all routes possible (all straight lines, not wavy curves, because Newton’s 1st law of motion holds inbetween quantum interactions!), but many of those routes cancel out as a result of interferences between the wave phases for those nearby virtual photons.
This is similar to what happens if you have two radio transmitter antenna and feed a signal into one and an inverted version of that signal into the other! The usual situation of a power transmission line with two conductors carrying alternating current is of this sort. The two radio waves superimpose to perfectly cancel each other out as seen from large distances, but when you are close to either antenna (within a range of up to a few times the distance between the antenna) the phases of the radio waves don’t perfectly interfere, and so very important effects – physically causing what is described by Maxwel’s equation for ethereal “displacement current” in a capacitor with vacuum as the dielectric, while it charges up or discharges – do actually occur. Because each of the two conductors in your mains power flex carries an inverted signal of that in the other, there is cancellation of the radiated 50 Hertz signal as seen from long distances. At short distances you can detect the 50 Hertz signal, because you’re near enough that the interference is not perfect (i.e., one conductor is significantly closer to you than the other). Also, if the power flex is near something conductive, the conductor reflects radio waves back that may prevent perfect interference, so some 50 Hz radio waves escape, causing a slight electric power loss. But generally, alternating current doesn’t result in power cords acting as 50 Hz antennas. This is because of phase vector cancellations, similar in general principle to the cancellation of paths far from that of least action in the path integral of quantum field theory.
Feynman states on a footnote printed on pages 55-6 of his book QED (Penguin, London, 1990):
“… I would like to put the uncertainty principle in its historical place: when the revolutionary ideas of quantum physics were first coming out, people still tried to understand them in terms of old-fashioned ideas … But at a certain point the old-fashioned ideas would begin to fail, so a warning was developed … If you get rid of all the old-fashioned ideas and instead use the [path integral] ideas that I’m explaining in these lectures – adding arrows [each arrow representing the phase vector contribution to the amplitude for one kind of reaction, embodied by a single Feynman diagram] for all the ways an event can happen [all Feynman diagrams and all geometric implementations of each spacetime Feynman diagram in three dimensional spatial geometry] – there is no need for an uncertainty principle!”
Feynman in QED points out that the effects usually attributed to the ‘uncertainty principle’ are actually due to interferences from virtual particles or field quanta in the vacuum (which don’t exist in classical theories but must exist in an accurate quantum field theory):
‘Light … ‘smells’ the neighboring paths around it, and uses a small core of nearby space. (In the same way, a mirror has to have enough size to reflect normally: if the mirror is too small for the core of nearby paths, the light scatters in many directions, no matter where you put the mirror.)’ – R. P. Feynman, QED, Penguin, 1990, page 54.
‘When we look at photons on a large scale … there are enough paths around the path of minimum time to reinforce each other, and enough other paths to cancel each other out. But when the space through which a photon moves becomes too small (such as the tiny holes in the screen), these [classical] rules fail – we discover that light doesn’t have to go in straight lines, there are interferences created by two holes … The same situation exists with electrons: when seen on a large scale, they travel like particles, on definite paths. But on a small scale, such as inside an atom, the space is so small that there is no main path, no ‘orbit’; there are all sorts of ways the electron could go, each with an amplitude. The phenomenon of interference [on small distance scales due to individual field quanta interactions not occurring in sufficiently large numbers to cancel out random chaos, and due to interactions with the pair-production of virtual fermions in the very strong electric fields on small distance scales, where the fields exceed the 1.3*1018 v/m Schwinger threshold electric field strength for pair-production] becomes very important, and we have to sum the arrows to predict where an electron is likely to be.’- R. P. Feynman, QED, Penguin, 1990, page 84-5.
‘… the ‘inexorable laws of physics’ … were never really there … Newton could not predict the behaviour of three balls … In retrospect we can see that the determinism of pre-quantum physics kept itself from ideological bankruptcy only by keeping the three balls of the pawnbroker apart.’ – Dr Tim Poston and Dr Ian Stewart, ‘Rubber Sheet Physics’ (science article) in Analog: Science Fiction/Science Fact, Vol. C1, No. 129, Davis Publications, New York, November 1981.
Hence, in the path integral picture of quantum mechanics – according to Feynman – all the indeterminancy is due to interferences. There is a physical mechanism for indeterminancy. It’s analogous to the indeterminancy of the motion of a small grain of pollen (less than 5 microns in diameter) due to jostling by individual interactions with air molecules, which represent the field quanta being exchanged with a fundamental particle. So what about alleged ‘wavefunction collapse’ leading to an infinite number of parallel universes and a metaphysical ‘quantum entanglement’ to explain Aspect’s experiment which shows that if you measure the polarizations of two photons metres apart, there is a correlation that either discredits causality (such as physical mechanisms)? The whole interpretation of the experiment using Bell’s theorem is wrong, because it’s missing out the actual mechanism for the correlation of photon spins when measured, and is falsely instead attributing the observed results to metaphysics due to poor mathematical physics. This is shown by Dr Thomas Love of the Departments of Maths and Physics, California State Unversity, stated in a preprint he kindly emailed me, Towards an Einsteinian Quantum Theory:
“The quantum collapse [in the mainstream interpretation of of quantum mechanics, which has wavefunction collapse occur when a measurement is made] occurs when we model the wave moving according to Schroedinger (time-dependent) and then, suddenly at the time of interaction we require it to be in an eigenstate and hence to also be a solution of Schroedinger (time-independent). The collapse of the wave function is due to a discontinuity in the equations used to model the physics, it is not inherent in the physics.”
Laws are rarely a true mechanistic model. They’re usually just approximations. E.g., when radioactive material decays it does so in discrete units of atoms, not as a continuous variable as in the exponential decay law, which is just a statistical approximation for large numbers. If you start with 3 radioactive atoms, you don’t have 1.5 radioactive atoms remaining after a half-life! It’s just a statistical approximation for large numbers, and an indicator of the probability of decay when the number of atoms is very small. It’s no use assuming it is a “true law” then adding a multiverse of uncheckable universes to the world in order to try to justify your flawed mathematics (continuous variables in a discrete world). If you use a bad mathematical model for the physical situation (i.e., you end up with a model which is only approximate for large numbers, big statistics), and then invent a multiverse of uncheckable parallel worlds to make your false mathematical physics consistent with an experimental result, you’ve totally failed as a scientist, because that’s what happens when a false model is fitted to reality: Ptolemy had to keep adding epicycles to the Earth-centred universe model to ‘explain’ away problems! The scientist has to ensure that the framework used to build a theory is secure, and the easiest way to go off into la la land is to start with a flawed mathematical model for the actual physical situation, and then “explain away” the failure by inventing a multiverse of unseen worlds. (I’ve added more about this problem in modern physics in the Appendix at the end of this blog post, below.)
The path integral as explained by Feynman (not the explanation by Wikipedia) is the resultant for a lot of interactions, just as the path integral was actually used for brownian motion (diffusion) studies in physics before its role in QFT. The path integral still has the problem that it’s unrealistic in using calculus and averaging an infinite number of possible paths determined by the continuously variable lagrangian equation of motion in a field, when in reality there are not going to be an infinite number of interactions taking place:
“It always bothers me that, according to the laws as we understand them today, it takes a computing machine an infinite number of logical operations to figure out what goes on in no matter how tiny a region of space, and no matter how tiny a region of time. How can all that be going on in that tiny space? Why should it take an infinite amount of logic to figure out what one tiny piece of spacetime is going to do? So I have often made the hypothesis that ultimately physics will not require a mathematical statement, that in the end the machinery will be revealed, and the laws will turn out to be simple, like the chequer board with all its apparent complexities.”
– R. P. Feynman, The Character of Physical Law, BBC Books, 1965, pp. 57-8.
” … Bohr … said: ‘… one could not talk about the trajectory of an electron in the atom, because it was something not observable.’ … Bohr thought that I didn’t know the uncertainty principle …”
– Feynman, quotation is from “The Beat of a Different Drum: The Life and Sciece of Richard Feynman”, by Jagdish Mehra (Oxford, 1994, pp. 245-248), see: http://www.tony5m17h.net/goodnewsbadnews.html#badnews
The first application of the path integral in physics was for working out Brownian motion, that is, the motion of a small (less than 5 microns in diameter) dust particle being hit at random by air molecules. The impacts induce a chaotic, random motion in the dust particle, making it move slowly in a process called diffusion. If on the average each impact of an air molecule against the dust particle makes it move distance s in a random direction, then after n impacts the dust molecule is most likely to be found in a random direction but at distance sn1/2 from the original starting point. The funny thing here is that we can predict how far the dust grain will move in a given time if we know the rate it is being struck and the average displacement due to each strike, even though we can’t predict what direction it will move in. (One of Einstein’s 1905 papers was about the calculation of Brownian motion.) This diffusive motion has important consequences for physics, for example in radiation transport for nuclear fireballs such as stars. The ionized gas in such fireballs is electrically conductive, so radiation is quickly absorbed and then reradiated in a random direction, and this process is repeated many times in lots of steps before the radiation gets to the surface of the fireball and can escape. The random or diffusive path is termed a ‘drunkard’s walk’.
Dirac became interested in the path integral because each step in a random walk was analogous to summing a phase contribution for a quantum field composed of many field quanta, and wrote a paper about it. However, it was Feynman who worked out how to apply it to quantum fields and mechanics in 1948, showing that it the motion of an electron in an atom was chaotic due to quantum field interferences which occur on small distance scales where there is not enough space for phases of individual interaction paths to cancel out. Feynman had a serious argument with Niels Bohr at the 1948 Pocono conference, where Bohr tried to dismiss the whole path integral approach to quantum field theory using Mach’s principle.
Despite these efforts, Feynman’s scientific approach to quantum mechanics has made little headway against the Bohr-ing mainstream political approach of Niels Bohr in the popular understanding of physics.
“Feynman proposed the following postulates:
- “The probability for any fundamental event is given by the square modulus of a complex amplitude.
- “The amplitude for some event is given by adding together the contributions of all the histories which include that event.
- “The amplitude a certain history contributes is proportional to
 , where
, where  is reduced Planck’s constant and S is the action of that history, given by the time integral of the Lagrangian along the corresponding path in the phase space of the system.
is reduced Planck’s constant and S is the action of that history, given by the time integral of the Lagrangian along the corresponding path in the phase space of the system.
“In order to find the overall probability amplitude for a given process, then, one adds up, or integrates, the amplitude of postulate 3 over the space of all possible histories of the system in between the initial and final states, including histories that are absurd by classical standards.” – http://en.wikipedia.org/wiki/Path_integral_formulation#Abstract_formulation
(However, as I explained above in this blog post, Wikipedia writers and many textbook authors are wrong to interpret “all possible histories” to include curved particle trajectories, because in quantum field theory there is no curvature in reality; just quantum interaction vertices which can make a lot of little straight lines look as if they approximate a curved trajectory. E.g., a light photon isn’t smoothly deflected along a curved geodesic, instead the trajectory only looks curved because there are many small deflections at discrete locations when gravitons interact with the photon via another – Higgs-type – field in spacetime. The “histories that are absurd by classical standards” are not curved paths, but histories that disobey the principle of least action, e.g. paths that still obey Newton’s 1st law of straight line motion in between quantum interactions, but which take longer paths than those which take the minimum time for a photon to reach it’s destination as observed by the target.)
The Feynman path integral (relative probability of an event occurring, or relative reaction rate) is ò DAeiS(A) where S(A) is the action, S(A) = ò d4xL, where L is the Lagrangian based on the gauge interaction equations for the kind of interaction (force field) being considered. For a classical Brownian motion drunkard’s walk, S(A) = ò (dx/dt)2dt. The role of S(A) = ò d4xL is to sum all possible actions over spacetime, which is necessary due to the physical principle of least action which is a variational principle that nature always takes the path which has the least action, generally the path which takes the least time.
So the path integral actually contains consists of two integrals, one within the other:
(1) One integral sums effective contributions for the infinite number of geometric paths that any particular 2-d Feynman diagram interaction (with a fixed number of interaction vertices) can actually be implemented in 4-d spacetime, weighted using a phase vector to determine the relative contribution from each path, while
(2) the main integral sums the interaction path histories for different Feynman diagrams (with differing numbers of interaction vertices)
Fig. 3: the path integral consists of two integrals, not one! As explained in his book QED, Feyman’s integal deals both with the many paths that can be taken by one kind of interaction. (Illustration credits: left-hand side diagram is from http://www.answers.com/topic/feynman-diagram?cat=technology; right-hand side diagram is based on Feynman’s book QED Figure 29.)
So you need to integrate not only all possible interactions (generic interaction histories are called Feynman diagrams and some are shown on the left hand side, a-j), but also all the ways that any given interaction type can actually take place in four dimensional spacetime (not the two dimensions of the idealized generic Feynman diagram).
Hence, each Feynman diagram (each kind of interaction, with a differing number of vertices) is actually a set of an infinite number of possible geometric ways that such an interaction can be accomplished in four dimensional spacetime. For example, the many different angles for the single vertex interaction on the right hand side of the diagram, where light gets refracted when entering the water because it’s velocity slows down, and to work out the angle of refraction you need to sum over all possible angles with a weighting that maximises contributions for paths which take the least time by cancelling out the other contributions (i.e., assigning them phase vectors that collectively add up to zero), because the effective path taken by light is that which takes the least time; all paths have equal contributions but differing phases which determine whether they add up or cancel out.
Generally, in low energy quantum field physics such as the approximate quantum field theories for long range gravity at low energy or low energy electromagnetism, the ‘loopy’ Feynman diagrams on the left hand side of the diagram above don’t contribute anything significant because the pair production creating the virtual fermion creation-annihilation loops in Feynman diagrams require higher energies than we normally experience in the physics of day-to-day life. So we don’t have to worry about looped Feynman diagrams when light gets refracted by water; we just use the simplest Feynman diagram and weight according to least action (time) all the possible ways it can be implemented geometrically. We would only have to take looped Feynman diagrams into account if we were using high energy gamma rays with a very short wavelength that can enter intense electromagnetic fields before an interaction occurs (Julian Schwinger worked out that there is no spontaneous pair-production in the vacuum if a constant electric field strength is below 1.3*10^18 volts/metre, which only occurs very close to charges like fermions, so only in high-energy physics do looped Feynman diagrams contribute substantially to interactions). In quantum gravity too, the low energy approximation doesn’t necessitate complex interactions; all you need to do is to sum all the contributions to the simplest type of graviton interaction (scatter) in order to approximate Newtonian gravity. You can do it geometrically just like Feynman analyzed low energy physics problems in his book QED.
The lagrangian based on the gauge field equations has to be integrated over spacetime to find the action for a specific Feynman diagram (i.e. all possible geometric gauge interaction histories corresponding to one Feynman diagram are summed). The amplitude for an interaction is a function of that action. Integrating the square modulus of the amplitude over all possible interactions (all Feynman diagrams) gives the total probability of all those interactions, which can be normalized to a probability of 1 if some reaction is certain (just as in quantum mechanics you get probability determined by integrating the square of the wavefunction over all of space, setting the result equal to 1 because you know the electron is somewhere in in space; having thus deduced the normalization constant, you can then happily perform other integrals to different radii to work out the absolute probability of finding the electron within this or that radius).
You can then analyze the relative contributions of different Feynman diagrams because the integral of the square modulus of the amplitude can be written as the sum of a series of term, each term representing one Feynman diagram.
You integrate all the paths that gauge bosons can take geometrically while conforming to one Feynman diagram, giving you the action for a Feynman diagram, and you use that action to integrate the square modulus of the amplitude over all possible Feynman diagrams to get the total path integral. Finding the perturbative expansion to the path integral then allows you to analyse the relative contributions of different Feynman diagrams to the amplitude or corresponding interacting cross-section in a particle physics experiment.
Integrating the lagrangian over spacetime is fine because the variety of absolute geometric paths of gauge bosons corresponding to any particular Feynman diagram is a continuous variable, well suited for integration. It’s however very undesirable to integrate over amplitudes for a variety of different Feynman diagrams (which don’t vary continuously from one to another; e.g. the number of vertices per Feynman diagram is always an integer, not a continuous variable).
It’s tempting to take the lagrangian for SU(2) with the Higgs field at low energy, and try modifying it so that half of the gauge bosons interact gain mass and interact with left-handed particles to give weak interactions, while half remain massless at low energy and produce long-range gravity and electromagnetic forces.
APPENDIX
In the example given above of using the exponential decay law to determine how many of the 3 original radioactive atoms remain after one half-live interval, the “multiverse interpretation” of quantum mechanics tries to “explain away” the prediction of 1.5 atoms by saying that two universes branch off, one in which there is 1 radioactive atom remaining and another in which there are 2 radioactive atoms remaining. The equation then gives an exact average of the different discrete numbers in different parallel universes. (To be precise, you can see that in reality there is some chance of two other possible results, e.g., there is a small probability that 0 of the three atoms will have decayed after one half life, and there is also a small probability that all 3 atoms will actually have decayed after just one half life.) However, this kind of physical extravagance – against Ockham’s Razon – of inventing extra universes to explain the failure of an approximate law that is based on observations for large numbers of events not small numbers of events is symptomatic of a deep problem in the culture of theoretical physics. It becomes dominated by mathematicians who view physics as being applied mathematics, rather than viewing the mathematics to be merely an approximate application of physical principles derived from nature.
So theoretical physics becomes dominated by a culture of speculative uncheckable orthodoxies, dogmas and frankly religious creeds, which have no physical content in them whatsoever, just like the mathematical models of Maxwell’s mechanical aether, Ptolemy’s epicycles, Kelvin’s vortex atoms, and other ad hoc guesses which were not grounded in reality but just sought to impose mathematics on speculative, non-factual interpretations. String theory’s anthropic landscape of 10500 universes is similarly an attempt to secure trashy physics. In string theory, the “speculative” – actually wrong – spin-2 graviton is added into particle physics by adding 6 extra spatial dimensions to the universe. These extra dimensions are not normally seen, so the theory has to get rid of them by making them invisibly small using such a device as a Calabi-Yau manifold. As you can guess, this 6 dimensional manifold’s exact parameters affect the way that the assumed very small strings can vibrate to produce fundamental particles. So you need to put into the theory the moduli for the sizes and shapes of the extra 6 dimensions in the Calabi-Yau manifold. You also need to have some Rube-Goldberg machine added to stabilize the manifold in any condition, to prevent the universe from spontaneously changing all the time which would be possible if the extra dimensions could vary or drift in size and shape.
Introducing all the unknown moduli for the 6-dimensional compactified manifold makes string theory produce 10500 different predictions of basic particle physics for the world we live in. This is really vague. If you paid me to predict tomorrow’s weather, and I “predict” a vast number of alternative scenarios with no way to pick out the right one without waiting to see the weather and then seeing which “prediction” was closest with the benefit of hindsight, you’d be angry, and you would not be impressed with the vast number of different predictions for the thing you want to know. Mathematically, if you have a model for something with a vast number of unknown parameters, you expect a vast number of solutions. This is called failure in physics. It’s a dead end. You can’t work backwards from nature to find the parameters of the Calabi-Yau manifold: consider the equation x2 = 4, and tell me definitely what x is. You can’t even work out a unique solution of one number for this very simple equation with just one variable from knowing the result is 4, because x could be either +2 or -2. So there is uncertainty over what the parameter really is, even when you know what the equation equals. If you have a six dimensional manifold it is a way more difficult situation and, if it works at all, you will have 10500 different predictions because there are 10500 different combinations of moduli possible to model the world.
Just because we know the real world, that alone does not imply that we can deduce the moduli in any sense uniquely. If we know x2 = 4, that doesn’t mean we can work out what x is uniquely: we have two possibilities, -2 or +2, and you don’t know which it is. It is this kind of thing that leads the more imaginative mathematical physicists to believe that the different solutions exist in different parallel universes, but that is not substantiated by facts. For string theory, you have many moduli for size and shapes of 6 unobservably small extra dimensions, and there is no way of determining those. Even if you could probe the enormous energy scales involved by using a particle accelerator the size of the galaxy, there would be uncertainty about which of the 6 extra spatial dimensions you were obtaining information about in each collision. You wouldn’t be able to read off all the sizes and shapes of the extra dimensions in the Calabi-Yau manifold. There would be inherent uncertainties remaining because there are just so many possibilities to explain any experimental results you get. It’s a failure. There is no objective scientific evidence whatsoever that the world is like that, there is just subjective speculation that makes no falsifiable predictions. There is evidence that string theory is wrong, because spin-2 gravitons are based on false physics, and graviton is predicted successfully by spin-1 gravitons. This is simply censored out by string theorists acting as ‘peer reviewers’ for non-string theory work they don’t bother to read.
Last word goes to the hero:
“It seems to me that Hossenfelder correctly analyzes the source of her difficulties: “The real problem I had, I think, is that I was bad at lying to myself.” Those more successful in the academic system sometimes criticize her as someone just not as talented as themselves at recognizing and doing good research work. But I see quite the opposite in her story. Many of those successfully pursuing a research career in this area differ from her in either not being smart enough to recognize bullshit, or not being honest enough to do anything about it when they do recognize bullshit.” – https://www.math.columbia.edu/~woit/wordpress/?p=13907



copy of a comment to Arcadian Functor:
http://kea-monad.blogspot.com/2008/07/origin-of-species.html
Thanks for the link to Tree Quantum Field Theory paper by R. Gurau, J. Magnen, and V. Rivasseau, which I read hoping for some physical insights. It starts very nicely by describing the limitations of the path integral. Page 2 of http://arxiv.org/PS_cache/arxiv/pdf/0807/0807.4122v1.pdf states:
“In this paper … we show how to base quantum field theory on trees, which lie at the right middle point between functional integrals and Feynman graphs so that they share the advantages of both, but none of their problems.”
The Feynman graphs represent physical processes albeit in a fairly abstract way. Any move away from them, towards greater mathematical abstraction, risks being a step away from concrete interaction modelling, towards some less physical mathematical abstraction. Page 3 adds:
“Model-dependent details such as space-time dimension, interactions and propagators are therefore no longer considered fundamental. They just enter the definition of the matrix elements of this scalar product. These matrix elements are just finite sums of finite dimensional Feynman integrals. It is just the packaging of perturbation theory which is redone in a better way. This is essentially why this formalism accommodates all nice features of perturbative field theory, just curing its single but giant defect, namely divergence.”
Divergencies are only a mathematical problem if you insist that cutoffs are unphysical. Actually, you get infinities everywhere in physics if you don’t use physically justified cutoffs to prevent absurb infinities. E.g., if you observe that the sun’s radiant power in watts per square metre varies as the inverse square law of the distance of the Earth from the sun, then you extrapolate to find the radiant power in the middle of the sun (zero distance), you get an infinity. In reality, the radiant power in the middle of the sun is not infinity; it’s the radiation flux associated with hydrogen fusion at 15 million K. The inverse square law here only works outside the sun. Once you start looking at what happens inside the sun, the physics changes and the mathematical inverse square “law” is no longer valid.
In the case of infinities at high energy (or small distances from fermions) in path integrals which require a cutoff, the divergences occur as you go towards zero distance because pair production charges would gain infinite amounts of momentum in the simple mathematical model, and as a result they would cause unphysical effects we don’t observe. The error here is that loops (pair production and annihilation) requires space for a pair of oppositely charged fermions to briefly separate before annihilating! Because you are going to smaller distances (less space) at higher energy, eventually the reduction in the available amount of space stops loops from forming. This means that there is a grain-size to the vacuum below which (or for physical collisions at energy above a cutoff corresponding to that grain size distance), you don’t get any loop effects because the space is too small for significant pair production and annihilation cycles to occur.
So I disagree that there is a physical problem with high energy divergences: it’s physically clear why there is a need to impose a cutoff at high energy to avoid infinities (i.e. renormalize charges to prevent running couplings from going to infinity or zero as zero distance is approached). It’s a pseudo-problem to try to get away from this by reformulating the physical model into more abstract concepts, a procedure which strikes me as akin to the old party game of trying to pin the tail on the donkey when blindfolded, e.g. pages 8-9:
“A QFT model is defined perturbatively by gluing propagators and vertices and computing corresponding amplitudes according to certain Feynman rules.
“Model dependent features imply the types of lines (propagators for various particles, bosons or fermions), the type of vertices, the space time dimension and its metric (Euclidean/Minkowsky, curved…).
“We now reorganize the Feynman rules by breaking Feynman graphs into pieces and putting them into boxes labeled by trees according to the canonical formula. The content of each tree box is then considered the matrix element of
a certain scalar product.”
The danger here is that you’re moving away from a physical understanding of what goes on in interactions, and it’s not clear from the paper that any benefit really exists. Rearranging the abstract mathematical model into a new form that causes the physical problems to be less clear is pure obfuscation! It’s mathematically wallpapering over the physical questions, not physically addressing them.
The Feynman graphs are the nearest thing you have to a depiction of a set of physical processes for what is really going on in producing forces, so this paper seems to be taking a step away from model building, and heading instead towards greater abstraction.
Even with the simplest mathematics, as soon as you get away from physical correspondence between the mathematics and the physical process, you get a great increase in possible mathematical models. This is the problem with all the speculations in physics: getting the mathematics to describe something that is too far from a physical process.
What I’d have loved to see is some effort in the opposite direction, trying to make the physical processes in the Feynman diagrams even more concrete, instead of breaking them up and forming a more abstract model.
The key Feynman diagrams for fundamental interactions at low energy only have two vertices. As Feynman shows in his book QED, the refraction of light by water is even simpler (for a swimmer underwater who sees a distorted position of the sun): path integrals describe it by just one vertice, namely the deflection in the light ray when it hits the water surface and is slowed down.
You work out the action for all paths with this one vertice (i.e., different angles), giving then different weightings for interference: the phase vector in the path integral maximises contributions from light paths that take the minimum time to travel from light source to the observer underwater. This is how the classical law of refraction (Snell’s law) emerges from the path integral with a varying phase vector for different paths.
I think it is therefore a mistake to try to look at Feynman diagrams with lots of vertices and turn them into a tree. The many vertex Feynman diagrams arise from pair production followed by annihilation, a “loop” cycle of physical processes. I don’t see how moving to more abstract territory will be an improvement, and this paper doesn’t seem to demonstrate any gains. Moving off the beaten track without a good reason is a recipe for ending up in quicksand. E.g., take a look at what happened to Dr Chris Oakley when he tried to build a quantum field theory without divergencies and renormalization: http://www.cgoakley.demon.co.uk/qft/. As soon as you move away from modelling the physical interactions and mechanisms for what is going on in quantum field theory, you will end up in a mathematical world of modelling things which are totally abstract rather than physical, and then you can’t make falsifiable predictions.
The problem is analogous to trying to someone realizing that the inverse square law for solar radiation irrationally predicts infinite energy density at zero distance from the middle of the sun, and then trying to guess a new mathematical law that gets around this problem, instead of simply imposing an arbitrary cutoff which acknowledges that the law breaks down at small distances. There is a large landscape of mathematical explanations and alternative model you could come up to replace an existing law. E.g., 1/r^2 can be replaced by 1/(X + r^2) or maybe 1/(X + r)^2, or many other such possibilities, where X is a small distance that has no effect on the inverse square law at big distances, but prevents it from giving infinity at zero distance from the middle of the sun.
But unless you are modelling the actual physical processes, the mathematics is guesswork. Also, if it happens that there is a large number of possible different mathematical reformulations, then there is a low probability of any one given alternative formulation is really going to be useful.
I wish this paper gave illustrations of which Feynman diagrams were being broken up and reassembled. If it were a case that physical Feynman diagrams were being reassembled individually in order to make calculations easier, then I could understand it. E.g. when you sum a lot of vectors you can add them in any order and the resultant vector is the same. If this was being done to make calculations easier, I could appreciate it. I wish category theory could be used to improve the path integral calculations.
“Perhaps most importantly it removes the space-time background from its central place in QFT, paving the way for a nonperturbative definition of field theory in noninteger dimension.”
This statement in the abstract conveys very abstract ambitions. But I haven’t been through all the maths in the paper because it’s technical and very time-consuming, so if I’m missing anything important, please let me know. (If this comment appears badly written or unhelpful, sorry and please delete it. I just don’t see what real physical problem it is solving by moving into more abstract territory.)
Atomic Model with Feynman Diagram decay
—> http://arnaudantoineandrieu.files.wordpress.com/2013/11/atomic_model_arnaudantoineandrieu.png
SuSy Model
—> http://arnaudantoineandrieu.files.wordpress.com/2013/12/susy_model_arnaudantoineandrieu.png
“Anyone with a knowledge of calculus and more than one brain cell knows that discontinuities cause problems to differential equations;”
For the record, it certainly takes a lot more than one brain cell to do calculus alone…