Update: the gravity mechanism diagram in this post is mis-drawn, so you should see the newer illustrations at the later posts:
https://nige.wordpress.com/2010/01/21/woit-and-the-spin-2-graviton-lie-of-pauli-and-fierz/
‘It’s a problem that physicists have learned to deal with: They’ve learned to realize that whether they like a theory or they don’t like a theory is not the essential question. Rather, it is whether or not the theory gives predictions that agree with experiment. It is not a question of whether a theory is philosophically delightful, or easy to understand, or perfectly reasonable from the point of view of common sense. The theory of quantum electrodynamics describes Nature as absurd from the point of view of common sense. And it agrees fully with experiment.’
– Richard P. Feynman, QED, Chapter 1, Princeton, 1985.
‘You might wonder how such simple actions could produce such a complex world. It’s because phenomena we see in the world are the result of an enormous intertwining of tremendous numbers of photon exchanges and interferences.’
– Richard P. Feynman, QED, Penguin Books, London, 1990, p. 114.
‘Underneath so many of the phenomena we see every day are only three basic actions: one is described by the simple coupling number, j; the other two by functions P(A to B) and E(A to B) – both of which are closely related. That’s all there is to it, and from it all the rest of the laws of physics come.’
– Richard P. Feynman, QED, Penguin Books, London, 1990, p. 120.
‘It always bothers me that, according to the laws as we understand them today, it takes a computing machine an infinite number of logical operations to figure out what goes on in no matter how tiny a region of space, and no matter how tiny a region of time. How can all that be going on in that tiny space? Why should it take an infinite amount of logic to figure out what one tiny piece of spacetime is going to do? So I have often made the hypothesis that ultimately physics will not require a mathematical statement, that in the end the machinery will be revealed, and the laws will turn out to be simple, like the chequer board with all its apparent complexities.’
– R. P. Feynman, The Character of Physical Law, November 1964 Cornell Lectures, broadcast and published in 1965 by BBC, pp. 57-8.
‘I would like to put the uncertainty principle in its historical place: When the revolutionary ideas of quantum physics were first coming out, people still tried to understand them in terms of old-fashioned ideas … But at a certain point the old-fashioned ideas would begin to fail, so a warning was developed that said, in effect, “Your old-fashioned ideas are no damn good when …” If you get rid of all the old-fashioned ideas and instead use the ideas that I’m explaining in these lectures – adding arrows [path amplitudes] for all the ways an event can happen – there is no need for an uncertainty principle!’
– Richard P. Feynman, QED, Penguin Books, London, 1990, pp. 55-56 (footnote). His path integrals rebuild and reformulate quantum mechanics itself, getting rid of the Bohring ‘uncertainty principle’ and all the pseudoscientific baggage like ‘entanglement hype’ it brings with it:
‘This paper will describe what is essentially a third formulation of nonrelativistic quantum theory [Schroedinger’s wave equation and Heisenberg’s matrix mechanics being the first two attempts, which both generate nonsense ‘interpretations’]. This formulation was suggested by some of Dirac’s remarks concerning the relation of classical action to quantum mechanics. A probability amplitude is associated with an entire motion of a particle as a function of time, rather than simply with a position of the particle at a particular time.
‘The formulation is mathematically equivalent to the more usual formulations. … there are problems for which the new point of view offers a distinct advantage. …’
– Richard P. Feynman, ‘Space-Time Approach to Non-Relativistic Quantum Mechanics’, Reviews of Modern Physics, vol. 20 (1948), p. 367.
‘… I believe that path integrals would be a very worthwhile contribution to our understanding of quantum mechanics. Firstly, they provide a physically extremely appealing and intuitive way of viewing quantum mechanics: anyone who can understand Young’s double slit experiment in optics should be able to understand the underlying ideas behind path integrals. Secondly, the classical limit of quantum mechanics can be understood in a particularly clean way via path integrals. … for fixed h-bar, paths near the classical path will on average interfere constructively (small phase difference) whereas for random paths the interference will be on average destructive. … we conclude that if the problem is classical (action >> h-bar), the most important contribution to the path integral comes from the region around the path which extremizes the path integral. In other words, the article’s motion is governed by the principle that the action is stationary. This, of course, is none other than the Principle of Least Action from which the Euler-Lagrange equations of classical mechanics are derived.’
– Richard MacKenzie, Path Integral Methods and Applications, pp. 2-13.
‘… light doesn’t really travel only in a straight line; it “smells” the neighboring paths around it, and uses a small core of nearby space. (In the same way, a mirror has to have enough size to reflect normally: if the mirror is too small for the core of neighboring paths, the light scatters in many directions, no matter where you put the mirror.)’
– Richard P. Feynman, QED, Penguin Books, London, 1990, Chapter 2, p. 54.
‘When we look at photons on a large scale – much larger than the distance required for one stopwatch turn [i.e., wavelength] – the phenomena that we see are very well approximated by rules such as “light travels in straight lines [without overlapping two nearby slits in a screen]”, because there are enough paths around the path of minimum time to reinforce each other, and enough other paths to cancel each other out. But when the space through which a photon moves becomes too small (such as the tiny holes in the [double slit] screen), these rules fail – we discover that light doesn’t have to go in straight [narrow] lines, there are interferences created by the two holes, and so on. The same situation exists with electrons: when seen on a large scale, they travel like particles, on definite paths. But on a small scale, such as inside an atom, the space is so small that [individual random field quanta exchanges become important because there isn’t enough space involved for them to average out completely, so] there is no main path, no “orbit”; there are all sorts of ways the electron could go, each with an amplitude. The phenomenon of interference becomes very important, and we have to sum the arrows [in the path integral for individual field quanta interactions, instead of using the average which is the classical Coulomb field] to predict where an electron is likely to be.’
– Richard P. Feynman, QED, Penguin Books, London, 1990, Chapter 3, pp. 84-5.
Sound waves are composed of the group oscillations of large numbers of randomly colliding air molecules; despite the randomness of individual air molecule collisions, the average pressure variations from many molecules obey a simple wave equation and carry the wave energy. Likewise, although the actual motion of an atomic electron is random due to individual interactions with field quanta, the average location of the electron resulting from many random field quanta interactions is non-random and can be described by a simple wave equation such as Schroedinger’s.
Feynman explains in his 1985 book QED how Newton discovered that the amount of light reflected from the front face of a block of glass depends on the number of wavelengths of light that can fit into the thickness of the glass block. Before the photon arrives at the block of glass, the electrons it it are oscillating due to interacting with one another by exchanging electromagnetic field quanta. The natural frequencies of oscillation of the electrons throughout the glass therefore depend on the thickness of the glass, because vibrations are continually propagating throughout the glass with many frequencies before the photon arrives, and only vibration waves which fit into the glass with an integer number of wavelengths reinforce each other optimally.
The oscillation frequencies which don’t have a wavelength that makes the block thickness correspond to an integer number of wavelengths, soon die out due to interference as they reflect off the edges inside the block. Just as the windows of an old bus rattle when the engine oscillations reach the natural frequency of vibration of the windows, a photon hitting the front of the block of glass where the electrons already (due to the block size) have certain natural periods of vibration, will have a likelihood of being reflected that depends on whether the block thickness divided by the wavelength of the photon is an integer or not. The photon does not have to travel right through the glass to discover how thick it is, divide the thickness into the wavelength, and decide whether to reflect. It just arrives at the front face of the glass block, and the glass thickness determines reflection probability since, long before the photon has even arrived, the thickness of the glass has already set up a natural frequency of vibration in the front electrons, due to the electron oscillations and field quanta exchanges in the glass:
‘When a photon comes down, it interacts with electrons throughout the glass, not just on the surface. The photon and electrons do some kind of dance, the net result of which is the same as if the photon hit only the surface.’
– Richard P. Feynman, QED, Penguin Books, London, 1990, Chapter 1, pp. 17.
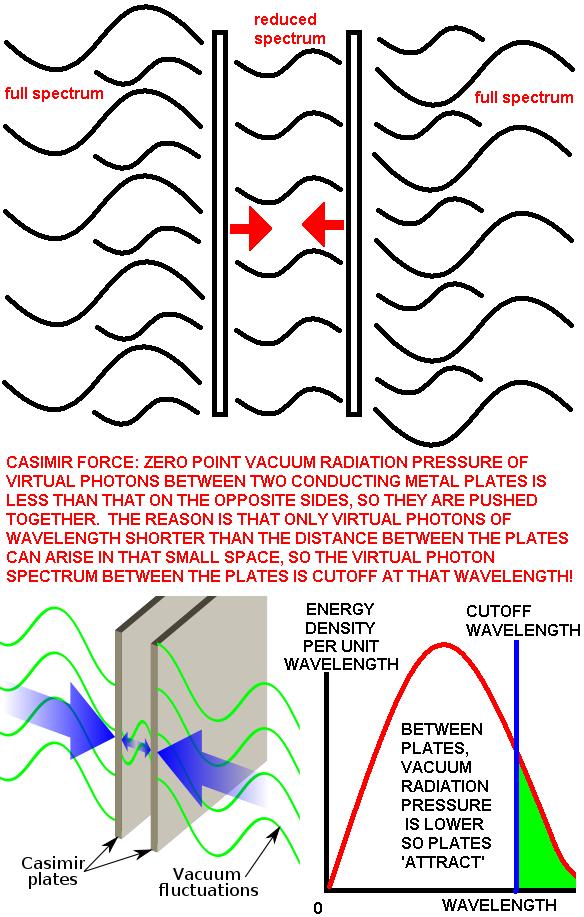
The paper by Professors Alfonso Rueda and Bernard Haisch, “Gravity and the Quantum Vacuum Inertia Hypothesis”, published in Annalen der Physik, vol. 14 (2005), pp. 479-498, provides an alternative to a Higgs field for generating mass: there are mass (i.e., acceleration-resisting and gravitational interaction) effects of a zero-point (off-shell) vacuum radiation field. E.g. inertia is due to radiation effects in the vacuum similar to the mechanism of the normal Casimir force (experimentally confirmed to 15% accuracy): virtual particles in the vacuum don’t just press metal plates together by excluding wavelengths that can’t fit between the plates, but they can also provide inertia (resistance to acceleration) and gravitation. The randomness of the virtual photons on small scales also causes the quantum indeterminancy, and impacts of such radiation on moving bodies will cause the contraction of moving bodies in the direction of motion and resistance to acceleration, but not continuous drag because the field quanta are off-shell virtual radiation.
The first empirically defended suggestion that inertia (Newton’s 1st law of motion) is due to some kind of field interaction between the mass in question and the masses surrounding it in the distant universe, was originally proposed by Ernst Mach on the empirical evidence of Foucault’s pendulum. Jean Foucault discovered in 1851 that a large pendulum hung from a high ceiling which is not constrained to swing along a fixed path (as in pendulum clocks) will naturally swing along a line which ‘rotates’ one revolution over the course of 24 hours: the path it swings is constant with respect to the distant stars, and the earth rotates underneath the pendulum. The only observable things that correlate with the plane of the pendulum are distant stars. Obviously, the stars are moving but their angular motion across the sky is negligible compared to the speed of the pendulum effect, and Ernst Mach pointed out that the observable reference frame for the inertia of the pendulum is the average distribution of matter in the surrounding universe. Mach rejected Newton’s old speculative and decrepid reference frame of invisible, unobservable ‘absolute space’ for determining accelerating motions (which restricted relativity doesn’t apply to, only applying to uniform motion) and replaced that ‘absolute space’ with an observation-based reference frame consisting of the observable average distribution of visible matter in the universe:
‘When … we say that a body preserves unchanged its direction and velocity in space, our assertion is nothing more or less than an abbreviated reference to the entire universe. … The considerations just presented show, that it is not necessary to refer the law of inertia to a spacial absolute space. … We may, indeed, regard all masses as related to each other.’
– E. Mach, The Science of Mechanics, Open Court, 1960, pp. 285-8.
Max Born in his book Einstein’s Theory of Relativity (Dover, New York, 1965, p. 362) suggests that Einstein applied general relativity to cosmology in 1917 on the basis of his equivalence principle between inertial and gravitational mass, assuming by Mach’s argument that mass in general will be determined by the distribution of the matter in the universe. In quantum gravity, gravitons are gravity field quanta exchanged between all masses as well as energy, so there is a graviton-mediated physical interaction between all masses, just as Mach argued using Foucault’s pendulum. Einstein:
‘… it … turns out that inertia originates in a kind of interaction between bodies, quite in the sense of your considerations on Newton’s pail experiment … If one rotates [a heavy shell of matter] relative to the fixed stars about an axis going through its center, a Coriolis force arises in the interior of the shell; that is, the plane of a Foucault pendulum is dragged around (with a practically unmeasurably small angular velocity).’
The 2005 Rueda-Haisch paper obtained a qualitative mechanism of shielding gravity for off-shell radiation, but they don’t make any checkable quantitative predictions because they don’t look at the balance of forces acting in the accelerating universe. They should also have discriminated gravitons from other vacuum field quanta with different force coupling constants, and introduced the factors which would make the mechanism yield checkable, quantitative predictions. In particular, the usual computation of the vacuum zero-point energy that causes the acceleration of the universe (i.e., the ‘dark energy’ of cosmology) is a massive overestimate, partly because it assumes Planck scale unification (discussed later) and partly because it implicitly and incorrectly assumes that the electromagnetic component (rather than just the graviton component) of the zero-point vacuum energy is causing the cosmic acceleration; the graviton field component of the zero-point energy naturally has a coupling constant only 10-40 that of electromagnetism for the low-energy physics of cosmological acceleration (supersymmetry assumes that unification and equality of couplings occurs at high energy, not low energy). Electrically neutral matter such as galaxies is accelerated by gravitons, not by electromagnetic field quanta that accelerate charged matter. For a technical explanation of quantitatively how this zero-point vacuum energy is miscalculated by a factor of 10120 or more for cosmic acceleration using the wrong field quanta component of the zero-point energy for low energy long range interactions using supersymmetry theory, see the about page. Nobel Laureate Sheldon Glashow was quoted commenting on their paper in New Scientist 13 Aug. 05, pp. 16-17: “This stuff, as Wolfgang Pauli would say, is not even wrong.”
Bare core QED force (i.e., not including the shielding factor due to vacuum polarization surrounding the core out to Schwinger’s cutoff at 33 fm from the centre of a unit charge like an electron)
Within 33 fm of a charged fermion (i.e. in electric fields stronger than the Schwinger cutoff for pair production), pairs of virtual fermions are created which annihilate into virtual radiation. The energy and duration, or the momentum and distance travelled, by such virtual radiation is modelled by the Heisenberg uncertainty principle.
Newton’s definition of force: F = dp/dt
where for static (equilibrium) forces exerted by light velocity field quanta such as virtual photons, r = ct or t = r/c, so F = dp/d(r/c) = c*dp/dr.
Heisenberg uncertainty principle (for minimum uncertainty): pr = h/(2*Pi), where p and r are uncertainties in momentum and distance, respectively. So p = h/(2r*Pi).
Hence, fundamental quantum field theory force F = c*dp/dr = c*d[h/(2r*Pi)]/dr = -hc/(2*Pi*r2).
This simple treatment produces a numerical prediction of the force strength together with producing the inverse-square law. Physically, this models the way that chaotic pair-production and annihilation in strong fields in the vacuum result in the emission of field quanta. Schwinger showed that the minimum electric field strength that is strong enough to disrupt the structure of the ground state of the vacuum and thereby cause spacetime ‘loops’ consisting of the endless cycle of pair-production -> virtual fermions of matter and antimatter -> annihilation -> virtual photons -> pair-production …, is 1.3*1018 v/m, which occurs up to a distance of 33 fm from a unit charge such as from the centre of an electron or proton. Inside this 33 fm radius, the vacuum is chaotic with particles colliding and annihilating at random, producing virtual radiation.
Notice that we have calculated the repulsive force between two electrons via quantum mechanics, and obtained a quantitative prediction complete with inverse-square law. When you compare this new result to the usual coulomb force prediction for the force between two electrons for low energy physics, you find that the force above from quantum mechanics (neglecting the vacuum polarization shielding of the core of an electron) is 1/alpha or about 137.036 times bigger than that from coulomb’s law. Hence vacuum polariation reduces the bare core charge of an electron by a factor equal to the fine structure constant. This large ~137 shielding factor implies that the running coupling for electromagnetism does not terminate at the speculative (unverified, merely dimensional analysis-based) Planck length of ~1.6×10−35 meters, but at a much more fundamental, smaller, more physically meaningful distance from the electron core, the black hole event horizon radius for the electron’s mass, 2MGc-2 ~ 1.4×10−57 metres. This vacuum polarization shielding factor support for the black hole scale of fundamental particles is a brand new result: Penrose for example speculates in his 2004 book Road to Reality that the bare core electron charge is just 1371/2 = 11.7 times the charge at low energy, on the basis that the formula for alpha (1/137…) is proportional to the square of the electronic charge. However, Penrose’s argument is just a numerological guess (rather like Planck’s inaccurate guess by dimensional analysis that the Planck length is the smallest physical size), unsupported by theory or experiment. As shown above, the quantum field strength is F = -hc/(2*Pi*r2), which is a factor of 1/alpha stronger than Coulomb’s law for two electrons, not a factor of (1/alpha)1/2 which would be the case if Penrose was correct. The physical importance of this result is that it substantiates the black hole core size for fundamental particles, which we will use below to make checkable predictions for quantum gravity.
In the previous post we explained that the exchange of a field quanta between real charges, with borrowed energy E delivered and re-emitted to produce a total momentum change in the real electron of p = E/c, just as in the reflection of light (where momentum E/c is delivered by impact and another E/c is delivered by the recoil when the new photon is emitted in the same direction as the incident photon, giving a total momentum of 2E/c), implies that Hawking’s radiation emission formula for black hole electrons correctly predicts electromagnetic forces.
Hawking’s formula for the radiating power of the black hole electron tells us it radiates with power P = 3 × 1092 Watts; but this is field quanta emission not real radiation for technical reasons. Hawking’s mechanism for black hole radiation emission omits Schwinger’s threshold field strength for pair-production in the vacuum, so only charged black holes produce field strengths above Schwinger’s threshold at the event horizon radius. The charge necessitated for black holes to emit radiation also changes the nature of the emitted radiation because it means that only positive virtual charges will fall into the electron core, and only negative virtual charges can be emitted.
The force of this radiation is the rate of change of the momentum, F = dp/dt ~ (2E/c)/t = 2P/c, where P is power. Hence, F = 2P/c = 2(3 × 1092)/c = 2 × 1084 Newtons. This is 1041 times the F = 1.8 × 1043 Newtons cosmological force (which by F = ma is the product of the cosmological acceleration of the universe and the mass of the accelerating universe) which gives rise to gravitation as proved below (see also the previous post) by Newton’s 3rd law, so this Hawking radiation force predicts the electromagnetic force strength, and is more empirical evidence that the cross-section for fundamental particles is the black hole event horizon size, not the Planck size.
This 137.036 (approx.) shielding factor applies to the vacuum polarzation region which extends from the bare core of an electron (believed by many people to be Planck size) out to the limiting distance for the pair production by a steady electric field, which is the IR cutoff and is predicted by Schwinger’s formula: 1.3*1018 volts/metre (equation 359 in Dyson’s http://arxiv.org/abs/quant-ph/0608140 or equation 8.20 in Luis Alvarez-Gaume, and Miguel A. Vazquez-Mozo’s http://arxiv.org/abs/hep-th/0510040). This electric field occurs out to 33 femtometres from the electron core, so all vacuum polarization (spacetime loops) and thus all vacuum shielding of electric charge occurs within 33 fm from the core of an electron.
The reason why alpha is a variable is vacuum polarization, e.g. at 91 GeV it falls from 1/137.036… to just 1/128.5 as reported in lepton collisions by Levine et al, in PRL, in 1997.
Alpha is the ratio of the low energy electric charge of an electron (i.e. the textbook charge for collisions and low energy physics generally below about 1 MeV energy, which corresponds to the required low-energy or IR cutoff on the logarithmic running coupling for QED interactions) to the bare core (high energy) charge of an electron. So if you collide particles hard enough that they penetrate part way through the shield, they experience a stronger (less shielded) force. This is why alpha is a ‘running coupling constant’. Just as the velocity of light is not a constant when compared for different transparent media, alpha is only a true constant for low energy physics, i.e. below the IR cutoff energy of ~1 MeV.
It is a true constant only when used to represent the total amount of shielding by the entire polarized vacuum, from the bare core charge to the low electron charge usually quoted in the textbooks for the case of a fully-shielded electron (i.e., for physics below the 1 MeV collision IR cutoff energy).

Above: fundamental forces are caused by the exchange of field quanta between charges. The light velocity gauge bosons or field quanta thus constitute the force fields around charges. The ‘virtual photons’ exchanged between electric and magnetic charges have 4 ‘polarizations’ and not just the 2 polarizations of real photons, because the force fields around an electron and around a proton are different; we observe the ‘charge’ of the fermion via the field so it appears that the 2 extra polariztions of virtual photons are electric charges (this doesn’t cause infinite magnetic self inductance and prohibit them being exchanged, because the magnetic field of the equilibrium return current of charged gauge bosons has a curl that cancels the magnetic field curl from the outgoing current; therefore only the one-way propagation of charged massless radiation is prohibited by the magnetic field problem which doesn’t exist for gauge bosons where there is an equilibrium of exchange with outgoing currents being matched by return currents).
We have never been able to observe ‘charge’ in any other way (no particle accelerator can ever approach the Planck scale, so we are always working with properties of fields, not the charged cores of fundamental particles themselves).

The Standard Model and mass (the charge for quantum gravity)
Noether’s theorem states there’s a symmetry for every conserved quantity, i.e. for every conserved charge. It is widely believed that all fundamental forces should unify, but the Nobel Prize was awarded for successes of electrweak theory in the low-energy “broken” regime where separate (short-ranged) weak and (long-ranged) electromagnetic interactions exist, not in the presumed unified high-energy regime above the presumed electroweak unification energy! The simplest model that fits observations is simpler than the Higgs symmetry breaking field, and is that the weak gauge bosons have mass at all energies (not just low energy as in the Standard Model). The massiveness of weak gauge bosons makes the weak force weak, so if you want running couplings to become identical above the “electroweak unification” energy, the weak gauge bosons need to lose their mass by a Higgs mechanism. But there is no evidence that nature does this; in fact the SM can’t even predict identical running couplings at the Planck scale for all forces even with a Higgs field (you need to add SUSY with 100+ additional parameters). The dogma of all running couplings becoming equal at the Planck scale leads only to ugly, non-falsifiable SUSY complexity.
There is empirical evidence that at higher energies (smaller distances) the Coulomb force running coupling or effective charge increases (e.g. it is 7% higher at 91 GeV than at low energy below the ~1 MeV IR cutoff), while the strong charge running coupling decreases as energy increases. Although gauge bosons are off-shell, the force fields they produce have a definite energy density so you can relate electric field strength at any distance from a quark to the energy density (J/m3) of that field. The running coupling increases the observable electric charge at high energy/short distances (seeing less of the polarized vacuum shielding effect), so that large bare-core electromagnetic charge when shielded by the cloud of polarized virtual fermions around it, deposits field energy in that shielding cloud which is what powers the short-ranged nuclear interactions. This fact based physical model will make falsifiable predictions because it’s built on observed facts, instead of containing 100+ unobservable parameters and many unobserved particles which can’t be predicted in a falsifiable way by supersymmetric theories (the supersymmetric theory doesn’t predict specific energies for those particles).
The Higgs field was, however, helpful to me for first getting a mechanistic model for gravitation. It is supposed to act like a “perfect fluid” in the vacuum, supposed to be composed of particles which don’t cause continuous drag, but only resistance to accelerations by “miring” particles. This mass-giving hebaviour is similar to the kind of gravitational charge needed to represent masses in the Tab tensor of general relativity:
“In many interesting situations… the source of the gravitational field can be taken to be a perfect fluid…. A fluid is a continuum that ‘flows’… A perfect fluid is defined as one in which all antislipping forces are zero, and the only force between neighbouring fluid elements is pressure.”
– Bernard Schutz, An Introduction to General Relativity, Cambridge, 1986, pp. 89-90.
Think of a submarine submerged. It has to push its own volume of water out of the way, causing an additional inertial resistance force to an acceleration. Behind the submarine, water flows into the same volume that the submarine is vacating as it moves. We know that water actually gets pushed out from the front, flows around, and pushes in at the rear. So, once the submarine is moving, the water flow adds additional momentum to the submarine.
Back in May 1996 we predicted cosmological acceleration a = Hc by applying Hubble’s empirical recession law to time since the big bang (illustrated below), which was confirmed observationally by NASA in 1998 (with no credit given), and we observed that particles accelerating radially from us will – by the fluid Higgs mechanism – result in an inward-directed Higgs motion, just as an array of submarines (or even swimmers!) accelerating outward from an observer underwater will be pushing water back, towards the observer. However, it has since become clear that the Higgs electroweak symmetry breaking field has problems, but the graviton (field quanta) and mass (gravitational charge) fields in the vacuum will do the same thing, so we began merely using Newton’s 2nd and 3rd laws to calculate outward force of accelerating matter F = ma and its resultant inward forces, predicting gravity:
Above: if two electrons of mass M were receding with cosmological acceleration a = Hc = 6 × 10-10 ms-2, their outward force F = Ma would be balanced – due to Newton’s 3rd law – by an equal and opposite i.e. inward-directed F = Ma gravitational repulsive force due to spin-1 graviton exchange between the masses. This is a repulsive force on the order of 10-39 Newtons, which is clearly wrong as Lubos says! But it is wrong because this gravitational repulsion of small masses is simply trivial compared to the overwhelming force of repulsion of them towards one another due to the inward force of F = ma = m(Hc) = 1.8 × 1043 Newtons from the graviton exchanges with m = 3 × 1052 kg of distant masses in the surrounding universe (according to NASA’s Hubble space telescope). The spin-1 quantum gravity predicts gravitational phenomena accurately, unlike string theory which isn’t even a quantitative prediction of the strength of quantum gravity (string theory is just qualitative agreement with spin-2 for gravitons, which we’ve disproved anyway).

Above: Edward Witten’s April 1996 ‘Reflections on the Fate of Spacetime’ in Physics Today included the claim that string theory ‘predicts gravity’ when it actually is just consistent with an unobserved spin-2 mode, claimed to be the spin of the graviton in a 1939 published Fierz-Pauli ‘proof’. Gravity is artifically forced to be attractive by the act of ignoring graviton exchange with all distant masses, instead of being treated with the beautifully simple predictive repulsion of similar charges: gravitons are simply pressing us down due to recoil from exchange with the immense masses of galaxies all around us in space, which makes the local repulsive exchange trivial by comparison. The Fierz-Pauli ‘proof’ simply ignored the fact that gravity charges in the surrounding universe will be exchanging gravitons with the two test masses, and there is no way to shield those exchanges to stop this from happening and save the spin-2 idea. Spin-2 means that the graviton has to look the same after 360/2 = 180 degrees rotation, so the outgoing and incoming gravitons look indistinguishable. This spin-2 idea is falsified by distant masses. (At least string theory’s gravity prediction turned out to be falsifiable after all!)
For quantum gravity, the surrounding mass of galaxies has the same gravity charge sign, so it will repel the two test charges. Further, incoming gravitons from distant immense masses will be converging (not diverging) so there will be geometric concentration, which will exceed the force from the local exchange of gravitons between two masses. Therefore, the incoming gravitons exchanged with the rest of the universe can push two masses together. This tragically means gravitons can have spin-1, not spin-2. Fierz and Pauli were negligent in ignoring the mass of the surrounding universe, using a defective oversimplified model! So string theory is inconsistent with a universe where we’re surrounded by immense mass whose converging (not diverging) incoming gravitons will push us down to earth; quantitative predictions of the spin-1 gravity coupling are possible and are successful. But string theorists are welcome to the holographic AdS/CFT correspondence as a consolation prize.
Above: discussion of graviton spin with the pathetically rude and deluded string theorist and former Harvard physics department assistant professor Lubos Motl, who is just one of many string theorists ignorant of the profound difference between classical (on-shell) hot radiation which can cause drag on moving objects like a gas, and virtual force-delivering radiation which is off-shell and doesn’t obey the classical laws of radiation, for instance it doesn’t heat up masses moving in a graviton (off-shell radiation) field, and it doesn’t slow down such moving masses by drag-effects.
This ignorance allows string theorists to simply ignore predictions using off-shell delivery of force:
Nige says: “Lubos, you ignored the physics of the mass in the surrounding universe exchanging gravitons with the two charges, pushing them together.”
Lubos Motl replies: “The reason why I ignored it is that it (a “third mass”) doesn’t influence the force between the two objects in any way. If you want to revive the 17th century Le Sage theory of gravity, see e.g. this page http://en.wikipedia.org/wiki/Le_Sage’s_theory_of_gravitation#Predictions_and_criticism why it’s wrong.”
Nige replies: “Dear Lubos, on-shell (real hot radiation) particles and off-shell (virtual) particles, are different. If the criticism against on-shell radiation also holds against off-shell radiation, then the arguments like drag will apply to all vacuum radiation including your beloved spin-2 gravitons.”
We know experimentally that these old objections simply don’t hold for off-shell particles, i.e. virtual radiations in the vacuum that cause fundamental forces. E.g., the Casimir force, experimentally confirmed to 15% accuracy, proves that vacuum radiation pushes metal plates together without causing drag or heating to moving bodies!
The Lorentz contraction and the inertia of bodies are due to graviton interactions, but off-shell field quanta moving with light velocity can’t be speeded up or slowed down like air molecules or dust hitting the nose of an aircraft. Thus, off-shell radiation thus heat up moving objects or cause drag, which would necessitate carrying away kinetic energy. They just cause a body to exert some radiation resistance to accelerations (inertia). An accelerating electron emits on-shell (hot) electromagnetic radiation and it also emits gravitational waves due to the acceleration of mass, although the gravitational waves carry on the order of 1040 times less energy due to the fact gravity is weaker than electromagnetism.
Other string theorists think similarly but prefer not to discuss the problems of string theory if at all possible
Professors Clifford Johnson (author of D-branes) and Jacques Distler (who works in string theory in Steven Weinberg’s department) both have blogs and I’ve been trying to understand their motivation for studying string theory. Do they really believe that there is any possibility of getting helpful physics out of a model of particles which has 6 compactified dimensions in a Calabi-Yau manifold so small that even in principle they can never be investigated to discover the hundred or so moduli (parameters of shape) they have, which are crucial for making predictions? The theory has so many unknown inputs that it produces a landscape of 10500 metastable vacuum states, or so, depending on how the unobservably small compactified extra dimensions are stabilized with charged “branes” by what is known technically as a “Rube-Goldberg mechanism” 😉 There is not even any known way to prove that our universe is included in the landscape of 10500 possibilities. There is no evidence that any of these possibilities are real, but the advocates of the theory believe and claim that all 10500 are real, and that they exist in that many unobserved parallel universes. Why do they proudly continue to work on it, when it looks such a massive failure, such a pseudoscientific belief dogma?
One idea from extra-dimensional string theory which is generating a lot of interest is that physics in an n dimensional space can be mathematically related to physics in a n – 1 dimensional space, allowing the understanding of one space to help with another. Maldacena’s holographic correspondence relates 5-d AdS (anti de Sitter space) as a “bulk” of n dimensions to conformal field theory of particles for QCD strong interactions or maybe condensed matter physics which can be represented by a 4-dimensional (mem-) “brane” with n – 1 dimensions. This should also hold for smaller numbers of dimensions, allowing “toy models” with a 2-d brane on a 3-d bulk to be modelled simply by the 2-d surface of an inflated balloon, filled with a “bulk” consisting of 3-d air. Another example is of course Edward Witten’s M-theory, where 11 dimensional supergravity (an unobserved spin-2 graviton theory in which there is supersymmetry present, so the graviton has a superpartner) is the bulk for a 10-dimensional supersymmetry of particle physics.
Think of a hologram: 3-d information is represented on a 2-d surface. But in order to view the 3-d information intrinsic in the 2-d representation, you need to move! Dr Jacob D. Bekenstein discovered that superstring theory in 5-d is equivalent to a conformal field theory of particles in the 4-d hologram, and that a black hole in the 5-d spacetime is equivalent to real (hot) radiation on the 4-d spacetime hologram (they have the same entropy, although it has a different origin).
Well, AdS has a negative cosmological constant (not the positive one observed) which would cause cosmological attraction (not the repulsion and outward acceleration observed by Perlmutter et al. from 1998 onwards). Therefore, AdS is junk cosmology. However, in nuclear physics AdS is useful over a certain range of distances because the pion-mediated strong nuclear force between nucleons is attractive with an effect similar to AdS! (The AdS/CFT correspondence is of course mathematically exact, but it will only be approximate when used to make predictions because the strong force is complex and over some distances the field quanta will not produce results that can be modelled accurately by AdS. This makes me wonder if the whole thing is being hyped far too much.)
So mathematically it may one day be useful to use the exact AdS/CFT correspondence as an approximation method for taking the field theory of the particles (CFT) and using it to calculate the force field geometry of the attractive force as a spacetime metric in AdS. This might allow some useful predictions for nuclear physics from QCD, which is notoriously difficult to deal with mathematically to make predictions, owing to the large coupling of the strong force, which causes a divergence – rather than a convergence – of successive terms in the perturbative expansion to a Yang-Mills QCD path integral for strong interactions, thereby necessitating non-perturbative methods like lattice approximations. It might also help to approximate the physics of other matter with similar properties, such as condensed matter, where the particles attract universally in order to condense.
It’s a very nice application of stringy ideas. But just because it may be useful (it has not won a Nobel prize yet, although that may not be far off), it isn’t a proof that string theory is correct regarding spin-2 gravitons over alternatives, or unification at the Planck scale. Professor Clifford Johnson has written:
“The tools … constitute quantum field theory, and we don’t need to declare whether or not the quantum fields and associated baggage (gauge symmetry, etc) are “out there” in Nature in some Platonic sense. Why bother? We are physicists and not philosophers. We need not (should not) confuse our tools with the things we are trying to describe with them. The same goes for string theory. If we find a place where string theory gives the best working description of the phenomena being studied and observed, why not just call it what it is? It is string theory that is being used, not “the tools of string theory”. There is no distinction.”
I responded (slightly tongue in cheek):
“Hope a big prize is soon awarded for the use of string theory’s AdS/CFT to solve problems in condensed matter physics or QCD strong interactions! Maybe when it starts getting prizes for applications, it will be seen in context more clearly, and will need less hype for unification and quantum gravity applications in popular media.”
I have the sneaking feeling, you see, that when some spin-off application of string theory is confirmed, Clifford will celebrate the confirmation of string theory, and we’ll get more suppression, not less, from mainstream “believers” in speculation. However, there is always the possibility that when string theory is celebrated for one application, the advocates will tone down their defensiveness of the speculative side of it, and be more understanding to other people.
On another post, Clifford commented upon a book called Why Does E = Mc2?:
“One of the interesting things was that there was a lot of amiable chatter around the science, but hardly any actual explanations. This was particularly marked when Simon tried to get them to explain E = Mc2, and I perked up since it sounded like there was going to be a very clever quick radio soundbite of Relativity and a snappy thought experiment to nail the concept, and I was all ready to be super-impressed by Brian Cox’s answer… but instead he punted it to “the theorist” Jeff Forshaw, who beat a bit about the bush for a while, and in the end it came down to the audience being told that… it’s in the book. To be fair, it was a tough job they had.”
I kind of take issue with this a bit, because Einstein never even addressed “why”; he just derived the equation. This is Mach’s argument to physicists to keep philosophy out of physics, because it is just noise that prevents communication and clear thinking:
“The question “why” surely is an unscientific question, just philosophy? Maxwell’s empirical equations of electromagnetism (based on experimental laws from Ampere for curl B, Gauss/Coulomb for div.E, and Faraday/Lenz for curl E) don’t contain any absolute motion dependence: e.g. you only get a magnetic field when there is a current (charge moving) relative to the observer, and that plus the fact that the velocity of light appears the same to all observers (as confirmed by the Michelson-Morley experiment) are the principles Einstein uses to derive E = mc2 mathematically.
“We don’t know why nature is the way it is. Models and equations are just convenience – predictive descriptions of observable phenomena. In biology you still have mechanisms like evolution, but basic physics is more mature and has dispensed with all mechanisms long ago. As far as mature physics is concerned, we’re not allowed to ask “why” questions, let alone come up with mechanisms to answer them.”

Above: the Feynman diagram and the path integral are behind the well-tested parts of physics, the Standard Model fundamental interactions. They’re not mathematical, e.g. Euler’s formula states that a simple path amplitude exp(iS) = (cos S) + i(sin S), allowing the path integral to be replaced by the summation of a series of arrows, one for each path, of constant length but varying direction: the resultant arrow is given by the straight line from the start of the first arrow to the tip of the last arrow, as Feynman shows when explaining path integrals without any equations in his 1985 book QED. The actual Feynman diagrams on the left involve only one distance in space and one in time, so every Feynman diagram represents the application of the depicted interaction over many paths in configuration space (shown on the right hand side for light being diffracted through water to reach an observer).
Light really does follow all paths, as can be shown – for example – by facts experimentally proved in the double slit experiment where a single photon is affected by the presence of both slits! That’s a fact! Notice that the Feynman diagrams above are also oversimplifications in that they don’t include the other particles in the surrounding universe which may be interacting with the two particles which are “attracted” or pushed together. E.g., the small space between two nearby nucleons (closer than one nucleon diameter apart) will slightly reduce the size of the virtual pion cloud inbetween those two nucleons, but the virtual pion clouds on the opposite sides of each nucleon will be unaffected, so they will tend to push the nucleons together over short distances by the “LeSage mechanism”. The same thing happens with the Casimir force, which is well tested to 15% accuracy.
The chaotic randomness of virtual particle exchanges is what makes quantum mechanics non-classical and non-deterministic: over small distances in the atom, an orbital electron (which is in a strong electromagnetic field and is also travelling around 1% of light velocity) exchanges field quanta randomly with other charges, so the Coulomb force acts a little like air molecules impacting upon a dust particle in Brownian motion, causing the electron to undergo somewhat chaotic motion and obey only a statistical wave equation rather than a simple classical orbit. (Bohm in 1954 derived the Schroedinger equation using Brownian motion; but notice the Brownian motion on small scales from field quanta we are dealing with is a well established fact of the well-tested Standard Model of particle physics such as the well-tested Casimir force of QED, totally unlike Bohm’s mysterious unobservable and hated “hidden variables”.)
Graviton exchanges with distant masses in the universe will have a similar effect, because almost all the mass is in the distant universe (clusters of galaxies, etc.) and gravitons exchanged with that surrounding mass will be concentrated as they converge inwards towards us. (The mainstream authors, such as Zee 2003, ignore the straight line path contributions to phase amplitudes depicted in Feynman’s QED book, and assume that the paths can go anywhere because they use a false argument that if you drill so many holes into screens screen that the screen disappears, particles can diffract anywhere. But diffraction by slits requires the real electrons at the edges of slits to interact with passing particles, so if you get rid of the screen altogether, diffraction will disappear and virtual particles will not be affected chaotically; Schwinger showed that virtual fermions can’t be formed in the vacuum unless you are close enough to a real charge that the field strength is 1.3 x 1018 v/m or more, the low energy IR cutoff limit for pair production and vacuum polarization. Therefore, the mainstream such as Zee’s book, are misleading themselves into neglecting the important physics that leads to physical predictions and is relatively simple. Gravitational effects on energy don’t cause significant deflections from straight line trajectories in everyday physics; even the mass of the sun had a trivial effect on the energy – or gravitational charge – of the starlight in the validation of a prediction of general relativity.)
In the previous post and (in far more technical detail) on the About page for this blog, there are some predictions made using the most simple physical concepts possible. How about trying the other way? Quantum gravity is incorporated into the Standard Model by a simple modification of the electroweak breaking Higgs field, so maybe we should present a paper on the mathematics of quantum field theory, dealing with the lagrangian field equations for the Standard Model interactions, their integration with respect to time to obtain the action for a particle interaction, and the integration of the exponential complex amplitude action over the configuration space to obtain the path integral. I would also have to go into the use of Noether’s theorem to connect the conservation laws of the different gauge symmetries to the Lagrangian field equations.
From http://www.ivorcatt.com/1_3.htm:
“a) Energy current can only enter a capacitor at the speed of light.
b) Once inside, there is no mechanism for the energy current to slow down below the speed of light.
c) The steady electrostatically charged capacitor is indistinguishable from the reciprocating, dynamic model.
d) The dynamic model is necessary to explain the new feature to be explained, the charging and discharging of a capacitor, and serves all the purposes previously served by the steady, static model.”
e) The static model, since it requires STATIC electric charge, suggests that the static electron needs to be replaced by some kind of light-velocity trapped electromagnetic current which behaves as an electron.
Gravitation is strong enough to trap light or electromagnetic energy waves into a trapped standing wave (an electron, or other fundamental, charged, spinning particle) where the original wavelength is smaller than the black hole radius for the original amount of mass-energy.
Once trapped in a black hole, the electron’s size and mass is fixed because it can only radiate and receive charged TEM wave radiation at the same rate:
The rate a black hole electron radiates energy per second is given by Hawking’s radiation formula and is almost ridiculous: 3 x 1092 watts, which predicts the electromagnetic force strength accurately. However, it can be proved that this is the rate at which all electrons are radiating charged radiation in the universe, and there is a perfect equilibrium of emission and reception.
This equilibrium exists in Ivor’s model in the magnetic self-inductance of charged light-velocity radiation: it cannot propagate unless there is equal amounts propagating in both directions so that the magnetic curl vectors of each component cancels the other out.
This equilibrium effect is vital for mainstream quantum field theory in the form of the Yang-Mills equation, which is a general equation that allows forces to be mediated by charged radiation exchange. The standard model of particle physics is just the Yang-Mills equation applied to charged radiations for strong and weak nuclear forces, and Maxwell’s equations for electromagnetism.
The form used for these equations is to as a Lagrangian which follows the energy of particles throughout an interaction. Integrating the Lagrangian energy over time gives the so-called action S for a path, and contributions from all paths are then summed by a Feynman path integral of the form exp(iS), which by Euler’s equation is (cos S) + i(sin S), so the action can be interpretated as an arrow of variable direction but constant length, and the path integral is a summation of such arrows or contributions from different paths, which allows for interference of paths. See Feynman’s 1985 book QED for a non-mathematical application of Standard Model path integrals to light, etc.
The Yang-Mills actually applies to electromagnetism, because the exchanged radiation between charges will itself be charged if the charge like the electron is trapped TEM energy with intrinsic charge. Hawking’s black hole radiation theory can’t be applied directly to a black hole electron because of the electric charge. Hawking assumes that radiation is emitted by unprejudiced escape of charges from pair production near the event horizon of an uncharged black hole. However, because the electron black hole will have a negative electric field and therefore appear as a negative charge to any observer, it will prejudice the escape of charge so that only negative radiation will be emitted. Thus, whereas in Hawking’s model the black hole radiation escaping is uncharged light for uncharged black holes, in the case of a negative electron you get the emission of only negatively charged radiation: the positively charged radiation caused by the pair production falls into the black hole. The equilibrium of emission and reception with other electrons in the universe keeps the charge and mass of the electron generally steady, although motion causes Lorentz type effects.
Now the importance of the contrapuntal model is that the Standard Model of particle physics contains Maxwell’s equations labelled U(1) and Yang-Mills equations labelled SU(2) for 2 electrically charged massive short ranged weak gauge bosons, W– and W+ (both observed at CERN, 1983), and SU(3) for three charges of strong nuclear forces.
This mechanism that Ivor asserts, that you have to have equal amounts of charged radiation going both directions at one time (an equilibrium) is what converts the Yang-Mills equation for charged radiation induced electromagnetic forces into the Maxwell equation for uncharged radiation exchange!
In other words, ALL fundamental forces, including electromagnetism, are mediated by the exchange of CHARGED radiation. The mainstream quantum field theorists wrongly believe that electromagnetism is mediated by UNCHARGED radiation. Therefore, they think falsely that they need Maxwell’s U(1) (unitary 1 or Abelian) symmetry for electromagnetism and Yang-Mills charged radiation special unitary SU symmetries 2 and 3 for nuclear forces!
If you put Ivor’s contrapuntal model for electromagnetism into the Standard Model of particle physics, you change it because U(1) is no longer electromagnetism: instead, electromagnetism comes from massless versions of electrically charged SU(2) gauge bosons, and the theory makes sense physically then because charged radiation exchange can push similarly charged electrons apart, and push oppositely charged electrons together, without needing the vague “4-polarization” radiation ad hoc fix of the mainstream for electromagnetic force mediating radiation.
Now what I’m trying to do is to work out what the true symmetry of the universe is. Massive SU(2) x SU(3) represents the short-ranged weak and strong nuclear forces of the Standard Model, and this is accurate and well tested. We need massless radiation SU(2) for electromagnetism, but we also need to include gravitation with mass being the fundamental charge for gravitational radiation forces to act upon. Since mass has only been observed to come with one sign of charge (all masses fall in the same direction!), gravitation should be a U(1) force.
So the Standard Model U(1) x SU(2) x SU(3) is actually the right mathematics but the wrong physics: the mainstream has made the following errors physically;
(a) The mainstream doesn’t realize that charges are trapped charged radiation, and that you get charged radiation emitted so electromagnetism is a charged radiation force modelled by the Yang-Mills SU(2) symmetry equation, not U(1) which is for uncharged radiation.
(b) The mainstream thinks that SU(2) is only for the weak forces and that ALL weak charged gauge bosons must be given mass by a separate, ugly, “Higgs field”, to prevent them from being long-range forces. Actually, only left-handed spin is affected by weak forces so it appears that only half of the charged radiations acquire mass and are responsible for weak nuclear forces; the other half don’t acquire mass and are instead long-range electromagnetism charged, massless radiation forces.
(c) The mainstream thinks that mass (gravitational charge) cannot be included in the Standard Model gauge groups because they can’t understand the symmetry needed for gravity, which they think needs spin-2 radiation to always be attractive for similar charges (all masses, gravitational charges, have the same sign so you would expect repulsion not attraction if the radiation spin was 1; the spin number is simply the number of symmetries for the radiation when it’s direction is rotated by 360 degrees, so spin12 means that if you rotate the radiation just 180 degrees it looks identical to how it did before rotating it, hence incoming and outgoing radiation for spin-2 would always cause attraction in the Fierz-Pauli theorem). This goes back to a 1939 paper by Fierz and Pauli.
However, that paper is based on a universe consisting of merely TWO charges exchanging radiation. It ignores the problem that gravity causing radiation will be exchanged with 3 x 10^52 kg of surrounding galaxies (NASA Hubble measurement of total mass of stars in universe: from page 5 of http://www.grc.nasa.gov/WWW/K-12/Numbers/Math/documents/ON_the_EXPANSION_of_the_UNIVERSE.pdf ).
I decided around January 2008 to go ahead with the project of putting this into quantum field theory, and obtained all the quantum field theory textbooks, including the widely recommended textbooks of of Ryder and Weinberg, as well as older books by Dyson and Dirac, and wacky newer books by authors Zee and McMahon. I also read Feynman’s original paper on path integrals, and the original Fiertz and Pauli paper claiming (incorrectly, by ignoring graviton exchanges with the mass of the universe surrounding any two masses under consideration) that gravity field quanta must be spin-2 for universal attraction. I also read various relevant arXiv papers introducing quantum field theory and the Standard Model.
It was over a decade since I had studied quantum mechanics, but I found quantum field theory more interesting. The reason I had studied quantum mechanics in the 1990s was because I had been duped into believing that it could calculate anything about atoms and nuclei to 15 decimal places, and was incredibly impressive. Towards the end of the course, after a lot of calculations that didn’t impress me at all, it became clear that quantum mechanics is more of an art than a science; the art of finding a good approximation as a simplified yet not too inaccurate model to calculate (the old applied physics art of ‘assuming a spherical cow as a first approximation, a cylindrical cow as a second, five cylinders as a third, five cylinders and a sphere as a fourth, …’): for every atom beyond hydrogen you are dealing with approximations because there are no analytical solutions. Even the ‘exact’ analytical solutions for the hydrogen atom ignore perturbative corrections for quantum vacuum effects, such as the possibility that a field quanta of the electromagnetic force binding the electron to the proton will interact in complex ways with virtual fermion loops near the proton or near the electron. In fact, there are an infinite number of possible ways that such interactions could occur, so you would need an infinite number of mathematical calculations to model all possibilities! Nature simply isn’t mathematical, it’s obvious. The few things calculated to 15 decimals were magnetic moments of leptons and the Lamb shift of hydrogen, and they were not quantum mechanics but quantum field theory which was not included on the course! Furthermore, it was clear that the calculations to that many decimals had taken large groups of physicists decades of work because of the complexity of calculating more and more complicated loop perturbative corrections from the vacuum field. Anyway, the reason for this blog post is the statement by Dr Peter Woit author of Not Even Wrong:
‘1. I firmly believe that at a fundamental level physics is based on deep mathematics, not on things that humans are readily able to visualize. The problem with string theory is not that it uses too sophisticated mathematics, it’s that it is a wrong idea about unification, and no amount of mathematical technology can fix this.
‘2. The problem with string theory is not that it can’t be tested today, but that it is inherently untestable, no matter how high an energy accelerator we ever figure out how to build. … In the case of string theory, in 1984 there was such a proposal, but what has been learned about the theory since then has shown that it doesn’t work, leading instead to landscape pseudoscience. … 25 years of research has just made the whole thing more and more implausible the more we learn.’
The sentence ‘I firmly believe that at a fundamental level physics is based on deep mathematics, not on things that humans are readily able to visualize’ is a piece of pseudoscientific prejudice. Who cares what anybody believes until they can prove that belief? In any case, what does he mean by ‘based on deep mathematics’? If it’s ‘based’ on deep mathematics, why isn’t there an exact analytical solution to any problem in quantum theory? We know enough about the mathematics of ordinary quantum mechanics to be able to see that physical reality cannot be based on mathematics; simply because it would require an infinite number of calculations to fully model even the very simplest quantum interactions that we see every day in the real world:
‘It always bothers me that, according to the laws as we understand them today, it takes a computing machine an infinite number of logical operations to figure out what goes on in no matter how tiny a region of space, and no matter how tiny a region of time. How can all that be going on in that tiny space? Why should it take an infinite amount of logic to figure out what one tiny piece of spacetime is going to do? So I have often made the hypothesis that ultimately physics will not require a mathematical statement, that in the end the machinery will be revealed, and the laws will turn out to be simple, like the chequer board with all its apparent complexities.’
– R. P. Feynman, The Character of Physical Law, November 1964 Cornell Lectures, broadcast and published in 1965 by BBC, pp. 57-8.
Possibly what had annoyed Feynman was propaganda from another Nobel Laureate, mathematical physicist Eugene Wigner, who gave a celebrated lecture on the ‘Unreasonable Effectiveness of Mathematics in the Physical Sciences’, published in Communications in Pure and Applied Mathematics, vol. 13, No. I (February 1960). However, a vital incident during Wigner’s own work during the Manhattan Project – conveniently not mentioned in his paper – illustrates why he is wrong. After Fermi had made the first nuclear reactor in Chicago in 1942, Wigner designed larger graphite moderated nuclear reactors to manufacture plutonium for atomic weapons. He knew the accuracy of the cross-sections of uranium, graphite and the other construction materials, and was proud to calculate the exact size.
It is well documented that he nearly resigned in anger when the engineers building the reactors increased the size of the reactor space to ‘allow for errors’. He argued that his physical data and mathematical calculations were reliable, and nobody had found an error. He was insulted and felt that the engineers didn’t understand nature, physics, mathematics and the ability to extrapolate from laboratory experiments on cross-sections to a full scale reactor. However, the engineers won and the reactors were built with room for extra uranium in case of unforeseen eventualities!
Now what do you think happened when the first full scale reactor started up with the amount of uranium Wigner had calculated? Yes. It failed. It worked for a few hours then spontaneously shut down! Wigner had missed out a vital piece of physics which hadn’t been seen in either Fermi’s low power (200 watt) reactor or in the laboratory fission experiments: large power reactors produce large amounts of a gaseous fission products like Xenon which are themselves effective absorbers of neutrons. Such gases escaped from small scale short-duration experiments lasting at most a few hours, and their properties were missed amid the 300 other fission products. But they became important and stopped reactor operation in a sealed high power reactor after about twelve hours of operation! This, to my mind, is a great illustration of the potential ineffectiveness of mathematics in the physical sciences, and the effectiveness of seat-of-your-pants mistrust of arrogant physicists by practical engineers. Of course mathematics is useful, but it isn’t any kind of substitute for religion. (If the engineers had done what Wigner insisted they should do, the plutonium bomb dropped on Nagasaki would have been delayed, and World War II would have continued longer.)
David Halliday and Robert Resnick state in Physics:
“If the [Newtonian] force laws had turned out to be very complicated, we would not be left with the feeling that we had gained much insight into the workings of nature.”
Sir Michael Atiyah also wrote on this topic in his article, “Pulling the Strings”, Nature, vol. 438, pp. 1081-2 (2005):
“The mathematical take-over of physics has its dangers, as it could tempt us into realms of thought which embody mathematical perfection but might be far removed, or even alien to, physical reality.”
Kea seems not to like this view of the problem of overly complex, elitist mathematics in physics, but I think that the category theory she is working with may be what is needed to reformulate QFT and solve all the outstanding problems of quantum gravity in a way which is more acceptible to the elite mainstream guys than my quantum gravity work which is just emulation of Feynman with a few ideas to make it produce the checkable predictions needed.
Category theory and Feynman’s path integral
In category theory you have “functors” which are processes that preserve and associate different mathematical structures or “categories”. Noether’s first theorem states that symmetries in the Lagrangian of a physical system are preserved by a conservation law. So symmetries and conservation laws are (by Noether’s first theorem)both “functors” which preserve and associate the different categories of fundamental particles in nature. “Morphisms” associate the fundamental particles in one category with those in another category. E.g., the act of painting a red car blue would be a “morphism” that would remove a red car from the scene and produce a blue car. Similarly, suitable “morphisms” to change the spin, mass and charges of fundamental particles would change them into one another. For example, neutrinos coming from the sun undergo “morphisms” that change them from one flavour into all three flavours by the time they arrive on earth, so that the experiments on the Earth which are designed to detect just the one flavour actually emitted from the sun in fact only detect 1/3rd of the amount emitted.
I hope that such methods will one day be used to replace the Feynman diagram and the sum over histories in configuration space (i.e. the path integral) with a more helpful system which will allow graviton contributions from distant masses to be included in quantum gravity, and will replace the existing Standard Model with a symmetry which incorporates gravitation. If category theory offered a better formal approach to replace all the elements of the Standard Model with discrete summations of interactions, computer calculations could simulate interactions, so you would have a discrete model for a discrete reality, instead of the current deeply flawed mathematical practice of using continuous techniques (calculus) to model discrete interactions. The current system requires discontinuities in the form of IR and UV cutoffs to be included for renormalization to get reasonable results; it would be much cleaner to build a model in which the physical phenomena of such cutoffs is present to begin with, instead of being manually inserted later to avoid infinities by forcing a continuous variable to include discontinuities at very low and very high energy.
Interesting predictions. There is some field that gives mass to particles in the gauge symmetries such as those of the SM, and since mass/energy is the charge of quantum gravity.
In general relativity a gravitational field has energy and is therefore a source of gravitation itself.
This causes quantum gravity to be looked at like some kind of Yang-Mills field where the field quanta must carry charge itself, i.e. the mainstream sees general relativity as evidence that quantum gravity is non-Abelian.
You would however expect from the fact that quantum gravity appears to involve only one sign of charge (mass-energy always falls downward in a gravity field) together with apparently just one type of field quanta, that quantum gravity is a simple Abelian U(1) gauge theory.
U(1) x SU(2) x SU(3) has to be supplemented with a Higgs field to break the U(1) x SU(2) symmetry thus separating the electromagnetic and weak forces by giving the weak forces mass.
Woit has made the point in his early blog post “The Holy Grail of Physics” that this electroweak symmetry breaking seems to go hand-in-hand with the way that the SU(2) field quanta which gain mass at low energy (limiting the range of the weak force to very small distances) also have the property of only partaking in left-handed interactions.
The left-handedness of the weak force seems due to an intrinsic property of the weak field gauge bosons. The simplest way to put quantum gravity and mass into the Standard Model is to leave the short range nuclear force SU(2) x SU(3) symmetry alone, but to change electromagnetism from U(1) to SU(2) with massless weak gauge bosons. I.e., half the weak gauge bosons gain mass to give the left-handed weak force; the remainder mediate electromagnetism. So you have negatively charged radiation mediating negative electric fields around electrons, instead of a neutral photon with 4 polarizations. The equilibrium of radiation exchange means that (1) magnetic curls cancel preventing the usual problem of infinite self-inductance for the propagation of charged massless radiation, and (2) this necessary perfect equilibrium of exchange physically prevents the charged field from affecting electric charges, so that the Yang-Mills equation for SU(2) electromagnetism automatically collapses effectively to Maxwell’s equations, since the Yang-Mills term for the charged field to modify fermion charges will be zero, and the equation is otherwise identical to Maxwell’s.
Hence, in SU(2) x SU(3) you then have electromagnetism, weak force and strong force. Because there is only need for one sign of gravitational charge (mass/energy) and one graviton, a U(1) theory can be added for quantum gravity and mass, with the U(1) field boson mixing with the neutral SU(2) field boson in the SM way to produce both a graviton and massive weak Z_0. I’d expect the massive U(1) gravitational charge to be identical to that of the Z_0, 91 GeV (already observed in 1983 at CERN).
Update:
‘I have here to again emphasize that I am only talking about people with good training [in mainstream methods] all the way through to a PhD. This is not a discussion about quacks or people who misunderstand what science is.’ – Professor Lee Smolin (click here for photo of him impersonating Einstein in a karaoke contest), The Trouble With Physics, Houghton Mifflin, New York, 2006, p. 370.
I think that this quotation is one thing from Smolin that Woit agrees with:
http://www.math.columbia.edu/~woit/wordpress/?p=2199
Is there a fundamental problem of representing the presumed spin-2 graviton using an SU(N) Yang-Mills gauge theory?
Fierz and Pauli showed that universal attraction of similar charges – mass/energy – requires a spin-2 field quanta, using two implicit assumptions you can easily disprove:
1. only two masses in the universe are assumed to exchange gravitons in the proof, so
2. the LeSage shadowing mechanism is automatically being ignored, despite the fact that all objections to LeSage only apply to on-shell real radiations, not off-shell virtual particles like gravitons
Is this spin-2 graviton the problem? Does this spin stop gravity being included by simply adding another gauge symmetry to the standard model to make it include gravitation? Hawking says:
“The real reason we are seeking a complete theory, is that we want to understand the universe, and feel we are not just the victims of dark and mysterious forces. … The standard model is clearly unsatisfactory in this respect. First of all, it is ugly and ad hoc. The particles are grouped in an apparently arbitrary way, and the standard model depends on 24 numbers, whose values can not be deduced from first principles, but which have to be chosen to fit the observations. What understanding is there in that? … The second failing of the standard model, is that it does not include gravity.”
– http://www.hawking.org.uk/index.php/lectures/91-godelendofphysics?format=pdf
I get the impression that spin-2 gravitons is a problem, and string theory is hyped as its solution since it includes spin-2.
Have you examined the [lack of] evidence for spin-2 gravitons either in theory or in practice?
The spin-2 gravitons will be interacting with the Higgs field (or its substitute) in the Standard Model, anyhow. The Higgs field isn’t given a gauge symmetry as as the charge for quantum gravity in the standard model. You say in your book that the Higgs field is called “Weinberg’s toilet”, but have you actually examined the fact that some such field is needed to supply mass as gravitational charge to the standard model?
Update on problems with the Higgs field
My argument is that the Standard Model is incomplete because it omits quantum gravity, which involves spin-1 gauge bosons as gravitons and a quantized unit charge. Quantum gravity is in this view like an Abelian U(1) field, not a Yang-Mills SU(N) field. The exchange of spin-1 gravitons produces a universal repulsive force; because it is bigger between an apple and the surrounding universe – with incoming gravitons converging inward from very large masses – than between an apple and the earth, the repulsion which predominates is the downward push. With much larger masses on all sides, such as galaxy clusters, the action of spin-1 gravitons is purely repulsive hence the cosmological acceleration of the universe.
There is no Higgs-type electroweak symmetry breaking as a function of energy as in existing electroweak theory; the symmetry is broken by a mass-giving field operating on half of SU(2) to give the left-handed massive weak gauge bosons of SU(2) at all energies; the remaining SU(2) gauge bosons remain massless and constitute charged electromagnetic fields. The Abelian group U(1) ceases to be the electromagnetism and becomes quantum gravity, a spin-1 graviton and a quantized 91 GeV massive gravitational charge which – after the Weinberg mixing of the gauge boson of U(1) with the uncharged Z gauge boson of SU(2) – couples via electromagnetic interactions (with reductions of mass caused thus by electromagnetic vacuum polarization effects) to the standard model charges. Tommaso Dorigo argued that mass should – in his view – couple via colour charge fields not electromagnetic fields, but we know in fact that leptons don’t appear to interact with colour charges under the energies so far used in experiments, while both leptons and quarks do undergo electromagnetic interactions. For more details on the prediction of fundamental particle (leptons and hadrons; individual quark masses aren’t isolatable even in principle) masses from the model, see the earlier post linked here.
Basically, the change is this: instead of an all-pervading Higgs field, we have instead a graviton field where gravitons are exchanged between 91 GeV gravitational charges which cluster around fermions in discrete numbers, and which mediate gravitational accelerations and resistance to accelerations (inertia) to particles with real mass (fermions and bosons) via electromagnetic interactions. This model is substantiated by the quantitative agreement of its predictions with measurements.




